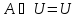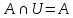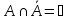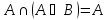- •По дискретной математике
- •0. Введение. Граф
- •Виды графов
- •Основная информация
- •Матрицы
- •1. Сеть. Потоки в сети. Теорема Форда — Фалкерсона
- •2. Функция. Бинарное отношение. Тотальность, сюръективность, инъективность, биективность. Примеры Множество
- •Бинарное отношение
- •Свойства бинарных отношений на множестве
- •Явное перечисление пар, определяющих бинарное отношение.
- •Задание процедуры проверки.
- •Задание матрицей смежности.
- •Задание графом.
- •Задание списком смежностей.
- •Функция
- •3. Бинарное отношение. Свойства. Матрица смежности и граф отношения. Отношение эквивалентности. Примеры
- •Отношение эквивалентности
- •4. Множество точек любой прямой имеет мощность континуума.
- •4. Алгебраическая структура. Полугруппа, моноид, группа. Примеры
- •Полугруппа
- •5. Группа. Абелева группа. Аддитивная группа. Мультипликативная группа. Конечная группа. Таблица Кэли. Циклическая группа. Декартово произведение групп Группа
- •Циклическая группа
- •Декартово произведение групп
- •6. Группа подстановок. Симметрическая группа . Умножение подстановок. Нейтральный элемент. Обратная подстановка. Число элементов группы Группа подстановок
- •7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа Цикл
- •Гомоморфизм. Изоморфизм. Теорема Кэли
- •8. Кольцо. Свойства. Коммутативное кольцо. Делители 0. Область целостности. Примеры. Подкольцо. Единица кольца. Поле. Примеры Кольцо
- •9. Идеал. Главный идеал. Теорема об идеалах поля (только и ). Следствие об идеалах в кольце Идеал
- •10. Сравнения. Классы вычетов по модулю (по идеалу ). Свойства. Малая теорема Ферма. Функция Эйлера. Теорема Эйлера (теория чисел) Сравнения
- •Свойства сравнений
- •11. Характеристика кольца. Теорема о характеристике кольца без делителей 0. Примеры. Кольцо классов вычетов. Примеры Характеристика кольца
- •12. Простой идеал. Необходимое и достаточное условие того, что идеал кольца — простой Простой идеал
- •13. Поле классов вычетов. Минимальное поле. Примеры Поле классов вычетов
- •14. Евклидово кольцо. Свойства (8 свойств). Примеры Евклидово кольцо
- •Свойства евклидовых колец
- •В евклидовом кольце все идеалы главные.
- •Любое евклидово кольцо содержит 1.
- •Если в евклидовом кольце ( делит ), но не делит , то .
- •15. Кольцо многочленов . Условия того, что кольцо — евклидово кольцо Кольцо многочленов
- •16. Приводимые и неприводимые многочлены в кольце . Примеры. Теорема о разложении в на произведение неприводимых множителей. Теорема Безу
- •17. Расширение поля (надполе). Теорема о том, что кольцо классов вычетов по модулю неприводимого многочлена есть поле. Степень расширения. Число элементов этого поля Расширение поля
- •18. Поле Галуа. Примеры полей Галуа как расширения полей. Таблицы сложения и умножения Поле Галуа
- •Литература
2. Функция. Бинарное отношение. Тотальность, сюръективность, инъективность, биективность. Примеры Множество
Множество
 — совокупность объектов
— совокупность объектов
 любой природы. Эти объекты называются
элементами множества.
любой природы. Эти объекты называются
элементами множества.
Символ
 — отношение принадлежности. Запись
— отношение принадлежности. Запись
 означает, что элемент
означает, что элемент
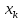 принадлежит множеству
принадлежит множеству
 .
Если элемент
.
Если элемент
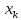 не принадлежит множеству
не принадлежит множеству
 ,
то пишут
,
то пишут
 (или
(или
 ).
).
Принцип
объёмности.
 означает, что множества
означает, что множества
 и
и
 состоят из одних и тех же элементов.
Пример:
состоят из одних и тех же элементов.
Пример:
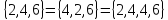 .
Но
.
Но
 .
.
Символ
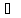 — отношение включения. Запись
— отношение включения. Запись
 означает, что каждый элемент множества
означает, что каждый элемент множества
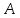 есть элемент множества
есть элемент множества
 .
То есть
.
То есть
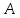 — подмножество множества
— подмножество множества
 .
.
Символ
 — отношение строгого включения (то
есть
— отношение строгого включения (то
есть
 ).
Запись
).
Запись
 означает, что каждый элемент множества
означает, что каждый элемент множества
 есть элемент множества
есть элемент множества
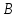 и
и
 больше
больше
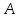 по количеству элементов. То есть
по количеству элементов. То есть
 — собственное подмножество множества
— собственное подмножество множества
 .
.
Заметим, что:
-
 .
. -
Если
 ,
то
,
то
 .
. -
Если
 ,
то
,
то
 .
.
Нельзя
смешивать понятия принадлежности и
включения. Хотя
 ,
,
 ,
но неверно, что
,
но неверно, что
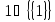 ,
а
,
а
 — верно.
— верно.
Пустое
множество
 — множество, не содержащее элементов.
Пустое множество есть подмножество
любого множества.
— множество, не содержащее элементов.
Пустое множество есть подмножество
любого множества.
У каждого множества есть два подмножества, которые называют несобственными — само множество и пустое множество. Все остальные подмножества — собственные.
Множество
всех подмножеств
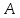 называется множеством-степенью (или
булеаном) и обозначается
называется множеством-степенью (или
булеаном) и обозначается
 .
.
Пример.
 .
Собственные подмножества
.
Собственные подмножества
 :
:
 ,
несобственные:
,
несобственные:
 .
.
Если
множество
 состоит из
состоит из
 элементов, то множество
элементов, то множество
 состоит из
состоит из
 элементов.
элементов.
Объединение
множеств ( )
— множество, все элементы которого
являются элементами множества
)
— множество, все элементы которого
являются элементами множества
 или
или
 :
:
 .
.
 .
.
Пример.
 .
.
Пересечение
множеств (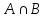 )
— множество, все элементы которого
являются элементами множеств
)
— множество, все элементы которого
являются элементами множеств
 и
и
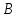 :
:
 .
.
 .
.
Очевидно,
что
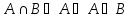 и
и
 .
.
Пример.
 .
.
Множества
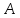 и
и
 — непересекающиеся, если
— непересекающиеся, если
 .
.
Разность
( )
— множество, все элементы которого
являются элементами множества
)
— множество, все элементы которого
являются элементами множества
 и не принадлежат множеству
и не принадлежат множеству
 :
:
 .
.
Пример.
 .
.
Симметрическая
разность ( )
— множество, каждый элемент которого
есть либо в
)
— множество, каждый элемент которого
есть либо в
 ,
либо в
,
либо в
 ,
но не в обоих.
,
но не в обоих.
 .
.
Пример.
 .
.
Универсальное
множество
 — множество всех рассматриваемых в
ходе данного рассуждения множеств.
— множество всех рассматриваемых в
ходе данного рассуждения множеств.
Дополнение
( )
— множество всех элементов
)
— множество всех элементов
 ,
которые не принадлежат множеству
,
которые не принадлежат множеству
 .
То есть
.
То есть
 .
Причём:
.
Причём:
 .
.
Пример.
 .
.
Прямое
(декартово) произведение ( )
— множество всех упорядоченных пар,
где первый элемент принадлежит множеству
)
— множество всех упорядоченных пар,
где первый элемент принадлежит множеству
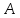 ,
а второй множеству
,
а второй множеству
 :
:
 .
.
Прямое
произведение
 множеств (
множеств ( )
— множество всевозможных упорядоченных
наборов из
)
— множество всевозможных упорядоченных
наборов из
 элементов
элементов
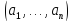 ,
где
,
где
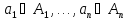 .
То есть
.
То есть
 Каждый такой набор элементов называется
кортежем. Произведение множества
самого на себя называется квадратом
множества и обозначается
Каждый такой набор элементов называется
кортежем. Произведение множества
самого на себя называется квадратом
множества и обозначается
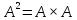 .
Аналогично
.
Аналогично
 -ая
степень
-ая
степень
 :
:
 .
.
Пример.
 .
.
Пример.
 .
.
Операция
 дистрибутивна (
дистрибутивна ( ),
но не коммутативна (
),
но не коммутативна ( )
и не ассоциативна (
)
и не ассоциативна ( ).
).
Диаграммы
Эйлера — Венна. На диаграммах Эйлера
— Венна множество
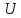 изображается прямоугольником, а множества
изображается прямоугольником, а множества
 — областями внутри прямоугольника. На
следующем рисунке проиллюстрированы
введённые определения операций над
множествами.
— областями внутри прямоугольника. На
следующем рисунке проиллюстрированы
введённые определения операций над
множествами.

Рисунок 13
Алгебра множеств — это пример булевой алгебры, поэтому все указанные далее (см. следующую таблицу) свойства операций следуют из свойств дизъюнкции, конъюнкции и отрицания.
Таблица 2
|
Свойства операций над множествами |
||
|
Идемпотентность |
|
|
|
Коммутативность |
|
|
|
Ассоциативность |
|
|
|
Дистрибутивность |
|
|
|
Свойства
|
|
|
|
Свойства
|
|
|
|
Свойства дополнения |
|
|
|
Законы поглощения |
|
|
|
Законы де Моргана |
|
|