18. Поле Галуа. Примеры полей Галуа как расширения полей. Таблицы сложения и умножения Поле Галуа

Поле Галуа — конечное поле, содержащее элементов. Обозначается .

Над полем вычетов (в поле — элементов) существуют неприводимые многочлены любой степени, поэтому кольца классов вычетов по модулю неприводимых многочленов образуют конечные поля любой степени над . Многочлены одинаковой степени приводят к одним и тем же (изоморфным) полям; никаких других полей из конечного числа элементов не существует.

Пример. В поле — всего 2 элемента. Многочлен 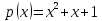— неприводим. Действительно:

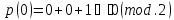
(то есть корней в 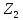нет)

Построим поле Галуа . Степень расширения равна 2. Элементов . Из . То есть в таблице умножения будем заменять на . Тогда элементы этого поля: . Построим таблицы сложения и умножения:

Таблица 7

Замечание. Легко убедиться в том, что в поле 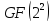все ненулевые элементы являются степенями одного элемента . Действительно, .

Теорема. Пусть — степень простого числа . Любой ненулевой элемент поля удовлетворяет уравнению: .

Доказательство.

Пусть — все ненулевые элементы поля . Возьмем любой элемент . Тогда — снова все ненулевые элементы поля. Следовательно, , отсюда . Теорема доказана.

Следствие. Любой элемент поля удовлетворяет уравнению . Для — простого это так называемая малая теорема Ферма:

для всех целых

Следствие. В поле многочлен 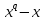раскладывается на линейные множители:

Следствие. При неприводимый многочлен делит многочлен , то есть , где , .

Теорема. В любом конечном поле существует (хотя бы один) элемент такой, что все ненулевые элементы этого поля являются степенями элемента : . То есть мультипликативная группа конечного поля является циклической группой порядка .

Доказательство. По первой теореме (текущего вопроса), любой ненулевой элемент поля является корнем уравнения 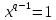. Но у многочлена степени не более корней. Поэтому равен числу ненулевых элементов поля. Но это и означает, что мультипликативная группа поля циклическая: существует такой элемент , что его порядок совпадает с порядком группы (и тогда все элементы группы являются степенями этого элемента).

Примитивный элемент конечного поля — элемент конечного поля, удовлетворяющий условиям предыдущей теоремы (то есть порождающий мультипликативную группу поля).

Примитивный многочлен — неприводимый многочлен, корнем которого является примитивный элемент.

Пример. Над полем многочлен является примитивным, так как любой его корень имеет 15 разных степеней: :

То есть все степени корня разные.

А неприводимый многочлен — не примитивен, так как любой корень этого уравнения (многочлена), очевидно, удовлетворяет уравнению :

То есть уже . Две степени корня совпали.

Таблица всех неприводимых многочленов полей , ,

Таблица 8

Поле	Количество элементов	Неприводимые многочлены
		Все неприводимые многочлены	Примитивные многочлены
	4
	8
	16
	32
	64
	9
	27
не простое число, поэтому не образует поля
	25
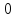
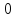
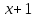
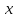
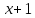
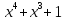
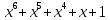
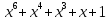
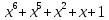
не простое число, поэтому не образует поля