Свойства евклидовых колец

1. В евклидовом кольце все идеалы главные.

Доказательство. Пусть — ненулевой идеал евклидового кольца . Выберем в элемент с наименьшей нормой . Тогда любой можно представить в виде , откуда . Не может быть так, чтобы ( с наименьшей нормой), следовательно, и .

2. Любое евклидово кольцо содержит 1.

Доказательство. Это следует из свойства I. Действительно, применим I к единичному идеалу. Тогда , откуда, в частности, следует, что при некотором . Докажем, что . Для любого получаем, что , то есть , то есть . Свойство доказано.

3. В евклидовом кольце любые 2 элемента и имеют НОД (наибольший общий делитель) , который представим в виде: , то есть НОД представим в виде линейной комбинации элементов и .

.

Доказательство. Рассмотрим множество . Это идеал (так как это сумма идеалов и ), это легко проверить непосредственно, то есть если взять любой элемент этого множества, умножить на любой элемент кольца, то снова попадаем в этот идеал.

Так как в евклидовом кольце любой идеал главный, то , следовательно такие, что и такие, что , то есть , так как — элементы идеала , то есть и , то есть — есть НОД.

4. В любом евклидовом кольце и тогда и только тогда, когда для некоторого обратимого элемента (то есть и ). В этом случае делится на и делится на .

Доказательство. Если и , то , откуда . Обратное утверждение очевидно, так как в этом случае из разложения вытекает, что .

5. Если в евклидовом кольце ( делит ), но не делит , то .

Действительно, если , то для некоторого , откуда по определению (строгое неравенство, так как 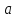не делит ).

6. В евклидовом кольце любой ненулевой необратимый элемент можно разложить в произведение простых сомножителей. (Доказывается при помощи индукции по .)

7. Если делится на простой элемент , то есть , то хотя бы один из сомножителей должен делиться на (иначе говоря, идеал — прост).

То есть если , то или .

Доказательство. Пусть не делит , то есть . Тогда , так как не делится на , иначе бы делилось на . Отсюда следует, что — обратим, так как — простое, следовательно . С другой стороны, по свойству №3: . Как видим, каждое слагаемое делится на ( делится на и делится на ), следовательно, делится на . Свойство доказано.

8. Отсюда из трёх последних свойств вытекает: все элементы евклидового кольца однозначно с точностью до обратимых элементов и порядка следования сомножителей разлагаются в произведение простых элементов.

15. Кольцо многочленов . Условия того, что кольцо — евклидово кольцо Кольцо многочленов

Многочлен (полином) от неизвестной над кольцом — выражение вида:

( полагаем равным .)

Элементы — коэффициенты многочлена; все они или их часть могут быть равны 0.

Степень многочлена — наибольшее такое, что . Обозначается: (). Если для всех , то .

Многочлен чисто символически обозначается , при этом не имеется в виду, что это отображение (функция).

Сумма и произведение двух многочленов определяются естественным образом:

— обозначение множества всех многочленов от с коэффициентами из .

Утверждение. Операции сложения и умножения определяют на множестве 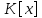структуру кольца, тем самым превращают в кольцо. Многочлены нулевой степени вместе с 0 образуют подкольцо констант , изоморфное кольцу .

Утверждение. Если — кольцо без делителей 0, то в имеет место равенство:

Это очевидно, так как старший член многочлена 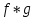— , где — старшие коэффициенты многочленов и соответственно, причём и , тогда старший член — (то есть ).

Следствие. Если — кольцо без делителей 0, то также не имеет делителей 0.

Утверждение. Для любого поля кольцо многочленов является евклидовым кольцом с нормой 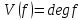. Действительно, в поле нет делителей 0, введённая таким образом норма удовлетворяет всем аксиомам нормы и алгоритм деления многочленов также введён.

Следствие. В кольце обратимы ненулевые константы, и только они.