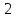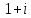- •По дискретной математике
- •0. Введение. Граф
- •Виды графов
- •Основная информация
- •Матрицы
- •1. Сеть. Потоки в сети. Теорема Форда — Фалкерсона
- •2. Функция. Бинарное отношение. Тотальность, сюръективность, инъективность, биективность. Примеры Множество
- •Бинарное отношение
- •Свойства бинарных отношений на множестве
- •Явное перечисление пар, определяющих бинарное отношение.
- •Задание процедуры проверки.
- •Задание матрицей смежности.
- •Задание графом.
- •Задание списком смежностей.
- •Функция
- •3. Бинарное отношение. Свойства. Матрица смежности и граф отношения. Отношение эквивалентности. Примеры
- •Отношение эквивалентности
- •4. Множество точек любой прямой имеет мощность континуума.
- •4. Алгебраическая структура. Полугруппа, моноид, группа. Примеры
- •Полугруппа
- •5. Группа. Абелева группа. Аддитивная группа. Мультипликативная группа. Конечная группа. Таблица Кэли. Циклическая группа. Декартово произведение групп Группа
- •Циклическая группа
- •Декартово произведение групп
- •6. Группа подстановок. Симметрическая группа . Умножение подстановок. Нейтральный элемент. Обратная подстановка. Число элементов группы Группа подстановок
- •7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа Цикл
- •Гомоморфизм. Изоморфизм. Теорема Кэли
- •8. Кольцо. Свойства. Коммутативное кольцо. Делители 0. Область целостности. Примеры. Подкольцо. Единица кольца. Поле. Примеры Кольцо
- •9. Идеал. Главный идеал. Теорема об идеалах поля (только и ). Следствие об идеалах в кольце Идеал
- •10. Сравнения. Классы вычетов по модулю (по идеалу ). Свойства. Малая теорема Ферма. Функция Эйлера. Теорема Эйлера (теория чисел) Сравнения
- •Свойства сравнений
- •11. Характеристика кольца. Теорема о характеристике кольца без делителей 0. Примеры. Кольцо классов вычетов. Примеры Характеристика кольца
- •12. Простой идеал. Необходимое и достаточное условие того, что идеал кольца — простой Простой идеал
- •13. Поле классов вычетов. Минимальное поле. Примеры Поле классов вычетов
- •14. Евклидово кольцо. Свойства (8 свойств). Примеры Евклидово кольцо
- •Свойства евклидовых колец
- •В евклидовом кольце все идеалы главные.
- •Любое евклидово кольцо содержит 1.
- •Если в евклидовом кольце ( делит ), но не делит , то .
- •15. Кольцо многочленов . Условия того, что кольцо — евклидово кольцо Кольцо многочленов
- •16. Приводимые и неприводимые многочлены в кольце . Примеры. Теорема о разложении в на произведение неприводимых множителей. Теорема Безу
- •17. Расширение поля (надполе). Теорема о том, что кольцо классов вычетов по модулю неприводимого многочлена есть поле. Степень расширения. Число элементов этого поля Расширение поля
- •18. Поле Галуа. Примеры полей Галуа как расширения полей. Таблицы сложения и умножения Поле Галуа
- •Литература
11. Характеристика кольца. Теорема о характеристике кольца без делителей 0. Примеры. Кольцо классов вычетов. Примеры Характеристика кольца
Характеристика
кольца
 с 1 — целое положительное число
с 1 — целое положительное число
 ,
для которого выполняется
,
для которого выполняется
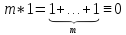 и никакое другое положительное число,
меньшее
и никакое другое положительное число,
меньшее
 ,
этим свойством не обладает. Если такого
,
этим свойством не обладает. Если такого
 нет, то говорят, что кольцо имеет
характеристику 0.
нет, то говорят, что кольцо имеет
характеристику 0.
Примеры.
-
Кольцо
 имеет характеристику 0, так как
имеет характеристику 0, так как
 ;
кольцо
;
кольцо
 также имеет характеристику 0.
также имеет характеристику 0. -
Кольцо
 ,
то есть множество классов вычетов по
,
то есть множество классов вычетов по
 ,
имеет характеристику
,
имеет характеристику
 .
Действительно
.
Действительно
 .
В частности, кольцо
.
В частности, кольцо
 ,
то есть множество классов вычетов по
модулю 3:
,
то есть множество классов вычетов по
модулю 3:
 ,
так как
,
так как
 ,
то есть характеристика
,
то есть характеристика
 равна 3.
равна 3.
Лемма.
Если характеристика кольца
 равна
равна
 ,
то для любого
,
то для любого
 .
.
Теорема. Характеристика любого кольца без делителей 0 (в частности, поля) либо 0, либо простое число.
Действительно,
если нет делителей 0, то есть нет таких
чисел
 ,
что
,
что
 ,
то из определения характеристики
,
то из определения характеристики
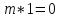 следует, что либо
следует, что либо
 ,
либо
,
либо
 — простое, так как в противном случае
— простое, так как в противном случае
 и, следовательно,
и, следовательно,
 ,
то есть имеются делители 0. Теорема
доказана.
,
то есть имеются делители 0. Теорема
доказана.
Следствие.
 — множество классов вычетов по
— множество классов вычетов по
 ,
где
,
где
 — не простое, имеет делители 0. Например,
— не простое, имеет делители 0. Например,
 имеет делители 0:
имеет делители 0:
 .
.
12. Простой идеал. Необходимое и достаточное условие того, что идеал кольца — простой Простой идеал
Простой
идеал
 в кольце
в кольце
 — идеал, в котором из
— идеал, в котором из
 следует, что либо
следует, что либо
 ,
либо
,
либо
 ,
либо оба.
,
либо оба.
Единичный
идеал
 — всегда простой, так как это само кольцо
— всегда простой, так как это само кольцо
 .
.
В
кольце целых чисел
 идеал
идеал
 прост при простом
прост при простом .
Так, например,
.
Так, например,
 — прост, так как
— прост, так как
 содержит числа кратные 3. Идеал
содержит числа кратные 3. Идеал
 — не прост, так как
— не прост, так как
 — не простое. Например,
— не простое. Например,
 .
.
Теорема.
Идеал
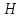 кольца
кольца
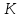 является простым тогда и только тогда,
когда кольцо классов вычетов
является простым тогда и только тогда,
когда кольцо классов вычетов
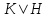 не содержит делителей нуля.
не содержит делителей нуля.
Доказательство.
Кольцо
классов вычетов
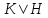 не имеет делителей 0 в том и только в том
случае, если из
не имеет делителей 0 в том и только в том
случае, если из
 ,
где
,
где
 ,
следует, что
,
следует, что
 ,
либо
,
либо
 ,
либо оба, но тогда: либо
,
либо оба, но тогда: либо
 ,
либо
,
либо
 ,
либо оба, что равносильно по определению
тому, что идеал
,
либо оба, что равносильно по определению
тому, что идеал
 — простой. Теорема доказана.
— простой. Теорема доказана.
13. Поле классов вычетов. Минимальное поле. Примеры Поле классов вычетов
Теорема.
(Следствие из предыдущей.) Кольцо классов
вычетов кольца целых чисел
 по модулю
по модулю
 является полем тогда и только тогда,
когда
является полем тогда и только тогда,
когда — простое число.
— простое число.
Примеры.
-
 .
Если
.
Если
 ,
то
,
то
 .
Если
.
Если
 ,
то
,
то
 ,
так как
,
так как
 .
Все ненулевые элементы имеют
противоположные, делителей нуля нет,
то есть
.
Все ненулевые элементы имеют
противоположные, делителей нуля нет,
то есть
 — поле.
— поле. -
 :
:
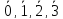 — есть делители 0, так как 4 — не простое.
— есть делители 0, так как 4 — не простое.
 ,
то есть
,
то есть
 — не поле.
— не поле.
Минимальное поле — поле, не имеющее подполей, отличных от него самого.
Примеры.
-
Поле рациональных чисел
 — минимально.
— минимально. -
Поля классов вычетов кольца целых чисел по простым модулям:
 — минимальные.
— минимальные.
14. Евклидово кольцо. Свойства (8 свойств). Примеры Евклидово кольцо
Евклидово
кольцо
 — кольцо
— кольцо
 без делителей 0, в котором каждому
ненулевому элементу
без делителей 0, в котором каждому
ненулевому элементу
 сопоставляется целое неотрицательное
число
сопоставляется целое неотрицательное
число
 ,
называемое нормой элемента
,
называемое нормой элемента
 ,
со следующими свойствами:
,
со следующими свойствами:
-
 .
. -
 ,
причём либо
,
причём либо
 ,
либо
,
либо
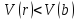 ,
либо оба (возможность деления с остатком).
,
либо оба (возможность деления с остатком).
Примеры.
-
Кольцо
 — евклидово кольцо с нормой
— евклидово кольцо с нормой
 .
Действительно,
.
Действительно,
 не имеет делителей нуля, а введённая
норма удовлетворяет условиям 1 и 2
определения:
не имеет делителей нуля, а введённая
норма удовлетворяет условиям 1 и 2
определения:
1)
 ,
если
,
если
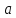 — целое, 2) деление с остатком введено.
— целое, 2) деление с остатком введено.
-
Кольцо
 целых гауссовых чисел
целых гауссовых чисел
 — евклидово кольцо с нормой
— евклидово кольцо с нормой
 .
Действительно:
.
Действительно:
-
 ,
если
,
если
 ,
то
,
то


и

-
Можно ввести деление с остатком. Например:
|
|
|
|
|
|
|
|
|
То есть
 .
Остаток:
.
Остаток:
 .
.
-
Кольцо многочленов от одной переменной
 с коэффициентами в поле
с коэффициентами в поле
 — евклидово кольцо с нормой
— евклидово кольцо с нормой
 равной степени многочлена
равной степени многочлена
 .
Действительно:
.
Действительно:
-
Пусть
 ,
,
 ,
тогда
,
тогда

-
Алгоритм деления многочлена на многочлен известен.
Пусть
 — любое кольцо без делителей 0. Говорят,
что
— любое кольцо без делителей 0. Говорят,
что
 делит
делит
 (то есть
(то есть
 делится на
делится на
 без остатка), если
без остатка), если
 такой, что
такой, что
 .
Запись:
.
Запись:
 .
.
Ясно,
что
 ,
то есть если элемент кратен
,
то есть если элемент кратен
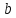 ,
то он кратен и
,
то он кратен и
 .
.
Простой
необратимый элемент
 евклидового кольца — необратимый
элемент евклидового кольца, который
допускает лишь тривиальное разложение,
то есть из равенства
евклидового кольца — необратимый
элемент евклидового кольца, который
допускает лишь тривиальное разложение,
то есть из равенства
 следует, что или
следует, что или
 ,
или
,
или
 обратимы. Например, в случае:
обратимы. Например, в случае:
 — тривиальные делители числа
— тривиальные делители числа
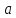 :
:
 и
и
 .
.
Любое
число
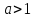 ,
у которого существует нетривиальное
разложение на множители, называется
составным.
,
у которого существует нетривиальное
разложение на множители, называется
составным.
Пример.
В кольце
 простые элементы:
простые элементы:
 …
Причём сомножитель этих чисел:
…
Причём сомножитель этих чисел:
 — обратим. Составные:
— обратим. Составные:
 …
(
…
( )
)