
- •По дискретной математике
- •0. Введение. Граф
- •Виды графов
- •Основная информация
- •Матрицы
- •1. Сеть. Потоки в сети. Теорема Форда — Фалкерсона
- •2. Функция. Бинарное отношение. Тотальность, сюръективность, инъективность, биективность. Примеры Множество
- •Бинарное отношение
- •Свойства бинарных отношений на множестве
- •Явное перечисление пар, определяющих бинарное отношение.
- •Задание процедуры проверки.
- •Задание матрицей смежности.
- •Задание графом.
- •Задание списком смежностей.
- •Функция
- •3. Бинарное отношение. Свойства. Матрица смежности и граф отношения. Отношение эквивалентности. Примеры
- •Отношение эквивалентности
- •4. Множество точек любой прямой имеет мощность континуума.
- •4. Алгебраическая структура. Полугруппа, моноид, группа. Примеры
- •Полугруппа
- •5. Группа. Абелева группа. Аддитивная группа. Мультипликативная группа. Конечная группа. Таблица Кэли. Циклическая группа. Декартово произведение групп Группа
- •Циклическая группа
- •Декартово произведение групп
- •6. Группа подстановок. Симметрическая группа . Умножение подстановок. Нейтральный элемент. Обратная подстановка. Число элементов группы Группа подстановок
- •7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа Цикл
- •Гомоморфизм. Изоморфизм. Теорема Кэли
- •8. Кольцо. Свойства. Коммутативное кольцо. Делители 0. Область целостности. Примеры. Подкольцо. Единица кольца. Поле. Примеры Кольцо
- •9. Идеал. Главный идеал. Теорема об идеалах поля (только и ). Следствие об идеалах в кольце Идеал
- •10. Сравнения. Классы вычетов по модулю (по идеалу ). Свойства. Малая теорема Ферма. Функция Эйлера. Теорема Эйлера (теория чисел) Сравнения
- •Свойства сравнений
- •11. Характеристика кольца. Теорема о характеристике кольца без делителей 0. Примеры. Кольцо классов вычетов. Примеры Характеристика кольца
- •12. Простой идеал. Необходимое и достаточное условие того, что идеал кольца — простой Простой идеал
- •13. Поле классов вычетов. Минимальное поле. Примеры Поле классов вычетов
- •14. Евклидово кольцо. Свойства (8 свойств). Примеры Евклидово кольцо
- •Свойства евклидовых колец
- •В евклидовом кольце все идеалы главные.
- •Любое евклидово кольцо содержит 1.
- •Если в евклидовом кольце ( делит ), но не делит , то .
- •15. Кольцо многочленов . Условия того, что кольцо — евклидово кольцо Кольцо многочленов
- •16. Приводимые и неприводимые многочлены в кольце . Примеры. Теорема о разложении в на произведение неприводимых множителей. Теорема Безу
- •17. Расширение поля (надполе). Теорема о том, что кольцо классов вычетов по модулю неприводимого многочлена есть поле. Степень расширения. Число элементов этого поля Расширение поля
- •18. Поле Галуа. Примеры полей Галуа как расширения полей. Таблицы сложения и умножения Поле Галуа
- •Литература
9. Идеал. Главный идеал. Теорема об идеалах поля (только и ). Следствие об идеалах в кольце Идеал
Левый
идеал — подкольцо
 кольца
кольца
 ,
в котором
,
в котором
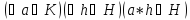 .
.
Правый
идеал — подкольцо
 кольца
кольца
 ,
в котором
,
в котором
 .
.
Двусторонний
идеал — подкольцо
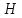 кольца
кольца
 ,
в котором
,
в котором
 ,
то есть подкольцо
,
то есть подкольцо
 кольца
кольца
 замкнуто относительно умножения на
любой элемент кольца.
замкнуто относительно умножения на
любой элемент кольца.
Когда
 — коммутативное кольцо, определения
левого, правого и двустороннего идеалов
совпадают. В таком случае используется
просто слово «идеал».
— коммутативное кольцо, определения
левого, правого и двустороннего идеалов
совпадают. В таком случае используется
просто слово «идеал».
Далее будем рассматривать только двусторонние идеалы и писать просто «идеал».
В
кольце
 всегда есть два несобственных идеала
—
всегда есть два несобственных идеала
—
 (нулевой идеал) и всё кольцо
(нулевой идеал) и всё кольцо
 (пишут «единичный идеал»:
(пишут «единичный идеал»:
 ).
То есть
).
То есть
 .
Все остальные идеалы — собственные.
.
Все остальные идеалы — собственные.
Примеры.
-
Множество чётных чисел
 образуют идеал в кольце
образуют идеал в кольце
 всех целых чисел. Действительно,
произведение любого чётного числа и
любого целого числа есть чётное число,
то есть принадлежит этому идеалу.
всех целых чисел. Действительно,
произведение любого чётного числа и
любого целого числа есть чётное число,
то есть принадлежит этому идеалу. -
Множество
 — идеал в кольце
— идеал в кольце
 .
. -
Множество квадратных матриц порядка
 с элементами из некоторого коммутативного
кольца
с элементами из некоторого коммутативного
кольца
 — некоммутативное по умножению кольцо,
поэтому в нём нужно различать односторонние
и двухсторонние (настоящие) идеалы.
— некоммутативное по умножению кольцо,
поэтому в нём нужно различать односторонние
и двухсторонние (настоящие) идеалы.
Пусть
дано коммутативное кольцо
 и
и
 .
Подмножество
.
Подмножество
 является идеалом в
является идеалом в
 ,
который называется идеалом, порождённым
элементами
,
который называется идеалом, порождённым
элементами
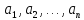 ,
и обозначается
,
и обозначается
 .
.
Главный
идеал
 — идеал кольца
— идеал кольца
 ,
состоящий из кратных элемента
,
состоящий из кратных элемента
 (то есть порождается одним элементом
(то есть порождается одним элементом
 ).
).
Кольцо главных идеалов — кольцо, в котором все идеалы главные.
Пример.
 — кольцо главных идеалов (все идеалы
имеют вид
— кольцо главных идеалов (все идеалы
имеют вид
 ,
то есть порождаются одним элементом
,
то есть порождаются одним элементом
 ).
Доказательство. Пусть
).
Доказательство. Пусть
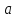 — произвольный идеал в
— произвольный идеал в
 .
Если
.
Если
 ,
то доказывать нечего. Если же в
,
то доказывать нечего. Если же в
 есть ещё элемент
есть ещё элемент
 ,
то
,
то
 содержит и элемент
содержит и элемент
 (исходя из определений кольца и идеала),
а один из этих элементов является
положительным числом. Пусть
(исходя из определений кольца и идеала),
а один из этих элементов является
положительным числом. Пусть
 — наименьшее положительное число в
идеале
— наименьшее положительное число в
идеале
 .
Если
.
Если
 — произвольное число в идеале
— произвольное число в идеале
 и
и
 — остаток от деления числа
— остаток от деления числа
 на число
на число
 (понятно, что
(понятно, что
 ),
то
),
то
 .
Так как
.
Так как
 и
и
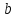 принадлежат идеалу
принадлежат идеалу
 ,
то число
,
то число
 тоже принадлежит этому идеалу. Так как
тоже принадлежит этому идеалу. Так как
 ,
то обязательно
,
то обязательно
 (
( — наименьшее положительное число в
идеале
— наименьшее положительное число в
идеале
 ).
Следовательно,
).
Следовательно,
 ,
то есть все числа идеала
,
то есть все числа идеала
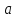 являются кратными числа
являются кратными числа
 .
Отсюда следует, что
.
Отсюда следует, что
 ;
следовательно,
;
следовательно,
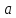 — главный идеал.
— главный идеал.
Пример.
В кольце
 также все идеалы главные, так как вместе
с любыми элементами
также все идеалы главные, так как вместе
с любыми элементами
 идеал всегда содержит их НОД.
идеал всегда содержит их НОД.
Теорема.
Любое поле не содержит идеалов, кроме
 и
и
 .
.
Доказательство.
Так
как в любом кольце всегда есть два
несобственных идеала:
 и
и
 ,
то любое поле также имеет два несобственных
идеала (любое поле является кольцом) —
это очевидно.
,
то любое поле также имеет два несобственных
идеала (любое поле является кольцом) —
это очевидно.
Пусть
 — ненулевой идеал в поле
— ненулевой идеал в поле
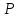 .
Так как
.
Так как
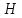 — ненулевой, то в нём есть элемент
— ненулевой, то в нём есть элемент
 .
В поле всякий ненулевой элемент
.
В поле всякий ненулевой элемент
 обратим:
обратим:
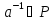 .
Тогда ввиду замкнутости
.
Тогда ввиду замкнутости
 относительно умножения на любой элемент
поля
относительно умножения на любой элемент
поля
 имеем:
имеем:
 .
То есть единица принадлежит идеалу
.
То есть единица принадлежит идеалу
 .
Тогда
.
Тогда
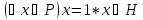 (ибо
(ибо
 ,
а
,
а
 — идеал). То есть
— идеал). То есть
 ,
и тогда, с учётом
,
и тогда, с учётом
 (по условию), имеем
(по условию), имеем
 .
То есть этот идеал
.
То есть этот идеал
 совпадает со всем полем
совпадает со всем полем
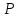 .
Таким образом, из предположения, что
идеал не является нулевым, мы вывели,
что он совпадает со всем полем. Теорема
доказана.
.
Таким образом, из предположения, что
идеал не является нулевым, мы вывели,
что он совпадает со всем полем. Теорема
доказана.
Замечание.
В любом кольце
 ,
отличном от поля, любой необратимый
элемент
,
отличном от поля, любой необратимый
элемент
 порождает идеал
порождает идеал
 ,
отличный от
,
отличный от
 и
и
 .
Например, так как в кольце
.
Например, так как в кольце
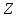 нет обратных элементов
нет обратных элементов
 (кроме
(кроме
 ),
то
),
то
 — не поле и в нём существуют идеалы:
— не поле и в нём существуют идеалы:
 …
…
Замечание.
Всякий идеал в кольце является подкольцом.
Обратное неверно. Например, кольцо
 целых чисел в поле
целых чисел в поле
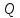 рациональных чисел является подкольцом,
но не идеалом.
рациональных чисел является подкольцом,
но не идеалом.
