
- •По дискретной математике
- •0. Введение. Граф
- •Виды графов
- •Основная информация
- •Матрицы
- •1. Сеть. Потоки в сети. Теорема Форда — Фалкерсона
- •2. Функция. Бинарное отношение. Тотальность, сюръективность, инъективность, биективность. Примеры Множество
- •Бинарное отношение
- •Свойства бинарных отношений на множестве
- •Явное перечисление пар, определяющих бинарное отношение.
- •Задание процедуры проверки.
- •Задание матрицей смежности.
- •Задание графом.
- •Задание списком смежностей.
- •Функция
- •3. Бинарное отношение. Свойства. Матрица смежности и граф отношения. Отношение эквивалентности. Примеры
- •Отношение эквивалентности
- •4. Множество точек любой прямой имеет мощность континуума.
- •4. Алгебраическая структура. Полугруппа, моноид, группа. Примеры
- •Полугруппа
- •5. Группа. Абелева группа. Аддитивная группа. Мультипликативная группа. Конечная группа. Таблица Кэли. Циклическая группа. Декартово произведение групп Группа
- •Циклическая группа
- •Декартово произведение групп
- •6. Группа подстановок. Симметрическая группа . Умножение подстановок. Нейтральный элемент. Обратная подстановка. Число элементов группы Группа подстановок
- •7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа Цикл
- •Гомоморфизм. Изоморфизм. Теорема Кэли
- •8. Кольцо. Свойства. Коммутативное кольцо. Делители 0. Область целостности. Примеры. Подкольцо. Единица кольца. Поле. Примеры Кольцо
- •9. Идеал. Главный идеал. Теорема об идеалах поля (только и ). Следствие об идеалах в кольце Идеал
- •10. Сравнения. Классы вычетов по модулю (по идеалу ). Свойства. Малая теорема Ферма. Функция Эйлера. Теорема Эйлера (теория чисел) Сравнения
- •Свойства сравнений
- •11. Характеристика кольца. Теорема о характеристике кольца без делителей 0. Примеры. Кольцо классов вычетов. Примеры Характеристика кольца
- •12. Простой идеал. Необходимое и достаточное условие того, что идеал кольца — простой Простой идеал
- •13. Поле классов вычетов. Минимальное поле. Примеры Поле классов вычетов
- •14. Евклидово кольцо. Свойства (8 свойств). Примеры Евклидово кольцо
- •Свойства евклидовых колец
- •В евклидовом кольце все идеалы главные.
- •Любое евклидово кольцо содержит 1.
- •Если в евклидовом кольце ( делит ), но не делит , то .
- •15. Кольцо многочленов . Условия того, что кольцо — евклидово кольцо Кольцо многочленов
- •16. Приводимые и неприводимые многочлены в кольце . Примеры. Теорема о разложении в на произведение неприводимых множителей. Теорема Безу
- •17. Расширение поля (надполе). Теорема о том, что кольцо классов вычетов по модулю неприводимого многочлена есть поле. Степень расширения. Число элементов этого поля Расширение поля
- •18. Поле Галуа. Примеры полей Галуа как расширения полей. Таблицы сложения и умножения Поле Галуа
- •Литература
Гомоморфизм. Изоморфизм. Теорема Кэли
Пусть
задано отображение
 группы
группы
 (с операцией
(с операцией
 )
в группу
)
в группу
 (с операцией
(с операцией
 ):
):
 .
Оно называется гомоморфизмом, если
оно одну групповую операцию переводит
в другую групповую операцию, то есть
если
.
Оно называется гомоморфизмом, если
оно одну групповую операцию переводит
в другую групповую операцию, то есть
если
 ,
,
 ,
,
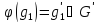 ,
,
 ,
то
,
то
 .
.
Изоморфизм
— взаимно однозначный (биективный)
гомоморфизм. Две группы
 и
и
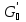 изоморфны, если существуют гомоморфизм
групп
изоморфны, если существуют гомоморфизм
групп
 и гомоморфизм групп
и гомоморфизм групп
 ,
такие что
,
такие что
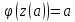 и
и
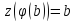 ,
где
,
где
 .
Запись:
.
Запись:
 или
или
 .
.
Свойства
изоморфизма ( ):
):
-
Единица переходит в единицу.
Имеем:
 .
.
Тогда:
 .
.
Аналогично устанавливаем, что
 .
.
Следовательно,
 — единица в
— единица в
 ,
а так как в группе
,
а так как в группе
 единица
единица
 единственна, то
единственна, то
 .
.
-
Обратный элемент переходит в обратный элемент.
Имеем:
 .
.
Тогда:
 .
.
Аналогично доказывается, что
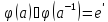 .
.
Следовательно,
 является обратным для элемента
является обратным для элемента
 .
.
Но в группе
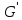 для элемента
для элемента
 обратный элемент
обратный элемент
 единственный.
единственный.
Следовательно,
 .
.
-
Обратное отображение
 тоже является изоморфизмом.
тоже является изоморфизмом.
Имеем:
 .
.
Так как
 ,
то
,
то
 .
.
Так как
 ,
то
,
то
 .
.
Следовательно,
 является изоморфизмом группы
является изоморфизмом группы
 на группу
на группу
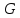 .
.
-
Композиция изоморфизмов — изоморфизм.
Пусть
 ,
тогда
,
тогда
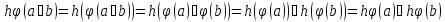 .
.
Примеры:
-
Отображение мультипликативной группы положительных действительных чисел
 на аддитивную группу всех действительных
чисел
на аддитивную группу всех действительных
чисел
 ,
при котором всякому
,
при котором всякому
 ставится в соответствие десятичный
логарифм этого числа
ставится в соответствие десятичный
логарифм этого числа
 ,
обладает свойством
,
обладает свойством
 ,
то есть является изоморфизмом.
,
то есть является изоморфизмом. -
Всякая бесконечная циклическая группа изоморфна группе целых чисел
 .
. -
Всякая циклическая группа порядка
 изоморфна мультипликативной группе
изоморфна мультипликативной группе
 корней
корней
 -й
степени из единицы.
-й
степени из единицы.
Теорема. Все циклические группы одного порядка изоморфны.
Теорема
(Кэли). Всякая конечная группа порядка
 изоморфна некоторой подгруппе
симметрической группы
изоморфна некоторой подгруппе
симметрической группы
 ,
то есть группе подстановок.
,
то есть группе подстановок.
Теорема Кэли, несмотря на свою простоту, имеет важное значение в теории групп. Она выделяет некий универсальный объект (семейство симметрических групп) — вместилище всех вообще конечных групп. То есть, согласно ей, изучение конечных групп может быть сведено к изучению групп подстановок.
8. Кольцо. Свойства. Коммутативное кольцо. Делители 0. Область целостности. Примеры. Подкольцо. Единица кольца. Поле. Примеры Кольцо
Кольцо
— множество
 с двумя бинарными операциями: сложение
«
с двумя бинарными операциями: сложение
« »
и умножение «
»
и умножение « »,
которые обладают следующими свойствами:
»,
которые обладают следующими свойствами:
-
Замкнутость:


-
Ассоциативность сложения и умножения:
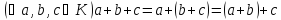

-
Коммутативность сложения:

-
Дистрибутивность умножения относительно сложения:


-
Существует элемент
 такой, что
такой, что
 .
Он называется нейтральным элементом
для сложения.
.
Он называется нейтральным элементом
для сложения. -
Существует для любого
 противоположный
элемент
противоположный
элемент
 для сложения такой, что
для сложения такой, что
 .
.
Коммутативное
кольцо — кольцо, в котором умножение
коммутативно, то есть
 .
.
Подкольцо
— подмножество
 кольца
кольца
 ,
если оно само является кольцом относительно
ограничения операций
,
если оно само является кольцом относительно
ограничения операций
 и
и
 на подмножество
на подмножество
 .
Для этого достаточно, чтобы
.
Для этого достаточно, чтобы
 удовлетворяло всем аксиомам кольца и
результаты сложения и умножения
принадлежали
удовлетворяло всем аксиомам кольца и
результаты сложения и умножения
принадлежали
 .
.
Кольцо
с 1 (единицей) — кольцо
 ,
в котором относительно операции умножения
существует нейтральный элемент «
,
в котором относительно операции умножения
существует нейтральный элемент « »:
»:
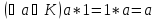 .
.
Иногда
под кольцом понимают только кольца с
единицей (то есть требуют, чтобы
подструктура была моноидом), но
изучаются также и кольца без единицы,
например, кольцо чётных чисел ( )
является коммутативным кольцом без
единицы.
)
является коммутативным кольцом без
единицы.
Замечание.
Кольцо
 относительно сложения образует
коммутативную группу, которая называется
аддитивной абелевой группой кольца.
относительно сложения образует
коммутативную группу, которая называется
аддитивной абелевой группой кольца.
Замечание.
Множество всех обратимых элементов
кольца
 с 1 относительно умножения образует
группу, которая называется мультипликативной
группой кольца.
с 1 относительно умножения образует
группу, которая называется мультипликативной
группой кольца.
Делители
нуля — элементы
 ,
принадлежащие кольцу
,
принадлежащие кольцу
 ,
для которых
,
для которых
 или
или
 .
.
Область
целостности — коммутативное кольцо
без делителей
 .
.
Некоторые математики требуют, чтобы области целостности имели мультипликативный нейтральный элемент (единицу). Поэтому далее в примерах «область целостности» будет обозначаться подробнее: с единицей ли она или без.
Обратная операция для сложения называется вычитанием, а её результат называется разностью (вычитание основано на аксиомах кольца — благодаря наличию обратных элементов по сложению):

Правила знаков (выводятся из аксиом кольца):
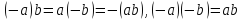
Умножение в кольце дистрибутивно относительно вычитания (также выводится из аксиом кольца):

Замечание.
Если один из сомножителей равен 0, то
произведение равно 0. Действительно,
 .
Обратное утверждение (справедливое для
чисел) неверно, то есть из того, что
произведение равно 0 не следует, что
один из сомножителей равен 0. (Например,
в случае с матрицами.)
.
Обратное утверждение (справедливое для
чисел) неверно, то есть из того, что
произведение равно 0 не следует, что
один из сомножителей равен 0. (Например,
в случае с матрицами.)
Замечание. Можно доказать следующие свойства:

Примеры.
-
Множество
 — область целостности без 1, а
— область целостности без 1, а
 — область целостности с 1.
— область целостности с 1. -
Множества
 (целые числа),
(целые числа),
 (рациональные числа),
(рациональные числа), (вещественные числа),
(вещественные числа),
 (комплексные числа) — области целостности
с 1 (коммутативны и не имеют делителей
нуля). Причём
(комплексные числа) — области целостности
с 1 (коммутативны и не имеют делителей
нуля). Причём
 — подкольцо
— подкольцо
 ,
,
 — подкольцо
— подкольцо
 ,
,
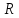 — подкольцо
— подкольцо
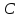 .
. -
Множество
 чётных чисел — область целостности
без 1.
чётных чисел — область целостности
без 1. -
Множество чисел, кратных
 :
:
 — область целостности. (В этом кольце
есть единица только при
— область целостности. (В этом кольце
есть единица только при
 .)
Причём
.)
Причём
 — подкольцо кольца
— подкольцо кольца
 .
. -
Множество нечётных чисел — не кольцо, так как нет замкнутости и нет
 .
. -
Множество квадратных матриц порядка
 с элементами из некоторого коммутативного
кольца
с элементами из некоторого коммутативного
кольца
 — просто кольцо с 1 (здесь уже
некоммутативное умножение на уровне
матриц и есть делители нуля). При
— просто кольцо с 1 (здесь уже
некоммутативное умножение на уровне
матриц и есть делители нуля). При
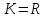 получаем кольцо квадратных матриц
порядка
получаем кольцо квадратных матриц
порядка
 над
над
 .
. -
Множество многочленов с коэффициентами из некоторого коммутативного кольца
 — область целостности с 1. При
— область целостности с 1. При
 получаем область целостности с 1
многочленов с целыми коэффициентами:
получаем область целостности с 1
многочленов с целыми коэффициентами:
 .
. -
Множество целых комплексных (гауссовых) чисел
 — область целостности с 1.
— область целостности с 1. -
Множество вещественных чисел специального вида
 — область целостности с 1.
— область целостности с 1. -
Множество
 (множество пар целых чисел
(множество пар целых чисел
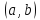 )
— коммутативное кольцо с 1, но с делителями
нуля (
)
— коммутативное кольцо с 1, но с делителями
нуля ( ),
если определены:
),
если определены:
-
Сложение:
 .
. -
Умножение:
 .
.
-
В кольце
 элемент
элемент
 — делитель 0:
— делитель 0:
 .
То есть
.
То есть
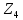 — коммутативное кольцо с 1, но с делителем
нуля.
— коммутативное кольцо с 1, но с делителем
нуля. -
Кольцо
 — область целостности с 1 тогда и только
тогда, когда
— область целостности с 1 тогда и только
тогда, когда
 — простое число. В частности,
— простое число. В частности,
 .
.
Поле
Поле
 — коммутативное кольцо с
— коммутативное кольцо с
 ,
в котором для каждого элемента
,
в котором для каждого элемента
 найдётся такой единственный обратный
элемент
найдётся такой единственный обратный
элемент
 ,
что
,
что

Подполе
— подмножество
 поля
поля
 ,
если оно само является полем относительно
ограничения операций
,
если оно само является полем относительно
ограничения операций
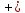 и
и
 на подмножество
на подмножество
 .
Для этого достаточно, чтобы
.
Для этого достаточно, чтобы
 удовлетворяло всем аксиомам поля и
результаты сложения и умножения
принадлежали
удовлетворяло всем аксиомам поля и
результаты сложения и умножения
принадлежали
 .
.
Поле без коммутативности умножения называется телом.
Замечание. Так как кольцо относительно сложения образует абелевую группу, то поле также образует группу, которая называется аддитивной абелевой группой поля.
Замечание. Относительно умножения все ненулевые элементы поля образуют группу, которая называется мультипликативной группой поля. Так как в поле умножение коммутативно, то эта группа поля также коммутативна.
Замечание.
Очевидно, что
 уравнения
уравнения
 и
и
 не имеют единственное решение, так
как
не имеют единственное решение, так
как
 и при
и при
 уравнения корней не имеют, а при
уравнения корней не имеют, а при
 имеют множество корней (
имеют множество корней ( — любое). Если же
— любое). Если же
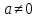 ,
то
,
то
 .
.
Замечание.
В поле нет делителей 0. Действительно,
пусть
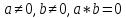 .
В поле существует
.
В поле существует
 ,
тогда
,
тогда
 ,
то есть противоречие, значит
,
то есть противоречие, значит
 — не делители 0.
— не делители 0.
Деление — обратная операция для умножения. Её результат — частное.
Обозначается:
 .
.
В любом поле:
-
 .
. -
 .
. -
 .
. -
 .
.
Можно
также положить
 и
и
 ,
то есть определить степени для любого
,
то есть определить степени для любого
 в поле.
в поле.
Примеры.
-
Множество
 — коммутативное кольцо без делителей
нуля, но не поле, так как отсутствует
1.
— коммутативное кольцо без делителей
нуля, но не поле, так как отсутствует
1. -
Множество
 — поле.
— поле. -
Множество
 не поле, так как нет обратных элементов
не поле, так как нет обратных элементов
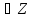 (кроме
(кроме
 ).
). -
 — поля. Причём
— поля. Причём
 — подполе поля
— подполе поля
 ,
а
,
а
 — подполе поля
— подполе поля

-
Множество матриц порядка
 — не поле, во-первых, некоммутативно
умножение, во-вторых, не для всех
элементов есть обратные (обратная
матрица есть только для невырожденных
(у которых определитель
— не поле, во-первых, некоммутативно
умножение, во-вторых, не для всех
элементов есть обратные (обратная
матрица есть только для невырожденных
(у которых определитель
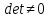 )
матриц).
)
матриц). -
Пары
 чисел
чисел
 — не поле (существуют делители 0).
— не поле (существуют делители 0). -
Множество комплексных (гауссовых) чисел
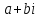 с
с
 — поле. Если же
— поле. Если же
 и
и
 — целые, то не поле (нет обратных
элементов).
— целые, то не поле (нет обратных
элементов). -
Множество вещественных чисел вида
 ,
где
,
где
 — поле.
— поле. -
Множество из двух элементов
 и
и
 —
—
 ,
если ввести операции сложения
,
если ввести операции сложения
 ,
,
 и умножения
и умножения
 ,
,
 — есть поле.
— есть поле. -
Кольцо
 — поле тогда и только тогда, когда
— поле тогда и только тогда, когда
 — простое число. В частности,
— простое число. В частности,
 — поле.
— поле.
