6. Группа подстановок. Симметрическая группа . Умножение подстановок. Нейтральный элемент. Обратная подстановка. Число элементов группы Группа подстановок

Пусть 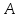— конечное множество из элементов: .

Симметрическая группа 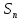степени — группа всех биекций (взаимно-однозначных отображений) множества в себя: . Число элементов (подстановок) симметрической группы: (число перестановок из ). Каждая биекция называется подстановкой (перестановкой) и записывается (природа элементов множества нас не интересует, значит можно считать, что элементы — числа):

Во второй строке записаны номера тех элементов, которым сопоставляются элементы из первой строки: . Поэтому в написанной матрице столбцы можно как угодно переставлять, подстановка останется той же.

Произведение двух подстановок и — результат проведения сначала первой из них, а затем второй (композиция отображений): .

Для этого представляют столбцы так, чтобы её первая строка совпадала со второй строкой ; тогда 1-ая строка есть первая строка , а вторая строка — есть вторая строка .

Некоторые математики иначе определяют произведение двух подстановок: . (Это связано с тем, что произведение подстановок, по существу, означает композицию отображений, а математики не пришли к общему соглашению насчёт обозначения композиции отображений.) Соответственно, из-за этого меняется порядок умножения, в итоге результаты разнятся. Поэтому необходимо заранее обозначать композицию так, как будете её использовать.

Пример. В данном примере показывается сама суть умножения подстановок.

Первая строка первой подстановки «взаимно-однозначно отображается на» вторую строку второй подстановки.

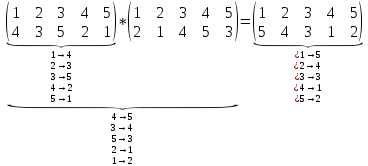
Пример.

Очевидно, что умножение перестановок ассоциативно, но не коммутативно.

Нейтральный элемент — это тождественная подстановка .

Обратный к это , так как .

Таким образом, множество подстановок -го порядка — множество, на котором введена замкнутая ассоциативная бинарная операция «умножение», на этом множестве есть нейтральный элемент, и все элементы этого множества обратимы, следовательно, множество подстановок образует мультипликативную группу. Эта группа называется симметрической группой степени и обозначается . Очевидно, что это конечная группа, и что порядок этой группы (число её элементов) равен .

Примеры.

1. Запишем все элементов (подстановок) симметрической группы :

;

2. Найти и :

Как видим , то есть умножение подстановок некоммутативно.

3. Найти обратную подстановку к и проверить:

7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа Цикл

Цикл длины — симметрическая группа степени , в которой элементы перемещены так, что (или, что то же самое, ), где все числа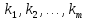 — разные, 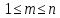. Цикл обозначается следующим образом:

или

Причём набор таких элементов называется орбитой любого из чисел .

Цикл независим, если у него нет общих чисел. Цикл длины 1 — это, очевидно, тождественная подстановка ; в произведениях подстановок их можно не записывать.

Теорема. Любую подстановку в можно записать в виде произведения независимых циклов. Разложение подстановки в произведение циклов длины определено однозначно с точностью до порядка циклов.

Доказательство.

Очевидно, что отношение между числами «принадлежность одной -орбите» есть отношение эквивалентности:

1. Рефлексивно, то есть .

2. Симметрично, то есть .

3. Транзитивно, то есть .

Данное отношение разбивает множество на классы эквивалентности по этому отношению. Каждый элемент принадлежит одному и только одному классу эквивалентности. Поэтому все числа однозначно разбиваются на непересекающиеся классы эквивалентных между собой орбит, а подстановка представляется как произведение соответствующих циклов. Теорема доказана.

Пример. .

Транспозиция — подстановка вида , где 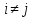, сводящаяся к перестановке двух чисел между собой, или, что тоже самое, цикл длины 2.

Любой цикл можно написать в виде произведения транспозиций:

Замечание. Транспозиции не коммутируют (как и перестановки).

Пример. .

Пример. .

Пример. .

Пример. .

Нетрудно показать, что любую подстановку можно представить в виде произведения транспозиций. Такое представление не единственно (например, в примерах выше ).

Все подстановки подразделяются на 2 класса: чётные и нечётные.

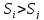Если в матрице подстановки есть 2 столбца , для которых и или и , то такая пара столбцов называется инверсией подстановки.

Подстановка называется чётной или нечётной в зависимости от того, чётно или нечётно число инверсий в ней.

Очевидно, что любая транспозиция является нечётной подстановкой:

одна инверсия нечётная

Теорема. Если подстановка чётная, то при любом способе разложения её в произведение транспозиций число множителей (то есть транспозиций) чётно, а если нечётная — то число этих транспозиций нечётно.

Следствие. Так как при перемножении чётных подстановок, очевидно, снова получается чётная подстановка, то множество всех чётных подстановок является подгруппой симметрической группы и называется знакопеременной группой и обозначается . Причём порядок равен . состоит из одной подстановки: . 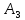состоит из подстановок и т. д.

Пример. Подгруппа симметрической группы состоит из 3-х подстановок:

Произведение двух нечётных подстановок, очевидно, есть чётная подстановка, поэтому нечётные подстановки не образуют группу.

Порядок подстановки — это наименьшее целое положительное число такое, что .

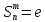Пример. Докажем, что порядок подстановки 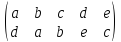равен 5:

Теорема. Порядок подстановки равен НОК длин всех её независимых циклов.

Также нетрудно показать, что порядок цикла равен длине цикла.

Пример. Определить, является ли подстановка чётной или нечётной и разложить её в произведение транспозиций:

Сосчитаем число инверсий . Инверсии — это пары столбцов , , , , , , . Поэтому 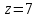(подстановка нечётная).

Разложим её на циклы:

Как видим, число транспозиций в произведении равно 5, то есть нечётно.

Обратная операция:

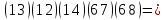
добавлена в середину только потому, что она равна . Другие подстановки (не равные ) в любое место добавлять нельзя, так как коммутативности нет.

Порядок подстановки: . То есть . Проверим это.