Экзаменационные вопросы © Kovalenko Leonid

По дискретной математике

Весь материал взят с книг и научных работ. Ничего не придумано☺

0. Введение. Граф 2

1. Сеть. Потоки в сети. Теорема Форда — Фалкерсона 12

2. Функция. Бинарное отношение. Тотальность, сюръективность, инъективность, биективность. Примеры 16

3. Бинарное отношение. Свойства. Матрица смежности и граф отношения. Отношение эквивалентности. Примеры 25

4. Алгебраическая структура. Полугруппа, моноид, группа. Примеры 30

5. Группа. Абелева группа. Аддитивная группа. Мультипликативная группа. Конечная группа. Таблица Кэли. Циклическая группа. Декартово произведение групп 37

6. Группа подстановок. Симметрическая группа . Умножение подстановок. Нейтральный элемент. Обратная подстановка. Число элементов группы 41

7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа 43

8. Кольцо. Свойства. Коммутативное кольцо. Делители 0. Область целостности. Примеры. Подкольцо. Единица кольца. Поле. Примеры 46

9. Идеал. Главный идеал. Теорема об идеалах поля (только и ). Следствие об идеалах в кольце 50

10. Сравнения. Классы вычетов по модулю (по идеалу ). Свойства. Малая теорема Ферма. Функция Эйлера. Теорема Эйлера (теория чисел) 51

11. Характеристика кольца. Теорема о характеристике кольца без делителей 0. Примеры. Кольцо классов вычетов. Примеры 56

12. Простой идеал. Необходимое и достаточное условие того, что идеал кольца — простой 56

13. Поле классов вычетов. Минимальное поле. Примеры 57

14. Евклидово кольцо. Свойства (8 свойств). Примеры 57

15. Кольцо многочленов . Условия того, что кольцо — евклидово кольцо 60

16. Приводимые и неприводимые многочлены в кольце . Примеры. Теорема о разложении в на произведение неприводимых множителей. Теорема Безу 61

17. Расширение поля (надполе). Теорема о том, что кольцо классов вычетов по модулю неприводимого многочлена есть поле. Степень расширения. Число элементов этого поля 62

18. Поле Галуа. Примеры полей Галуа как расширения полей. Таблицы сложения и умножения 63

Литература 68

0. Введение. Граф

Граф (в широком смысле) — конечный набор объектов любой природы, которые называются вершинами, некоторые пары из которых могут быть соединены.

Граф — множество вершин 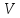и набор 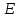неупорядоченных и упорядоченных пар вершин, где 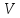— 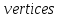, — . Обозначается . Неупорядоченная пара вершин называется ребром, упорядоченная пара — дугой.

Смежные (соседние) вершины — две вершины, которые соединены ребром.

Смежные (соседние) рёбра (дуги) — два ребра (две дуги), у которых есть общая вершина.

Кратные рёбра (дуги) — рёбра (дуги), соединяющие одну и ту же пару вершин.

Петля — ребро, которое начинается и кончается в одной и той же вершине.

Инцидентность — понятие, используемое только в отношении ребра (дуги) и вершины: если 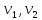— вершины, а 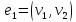— соединяющее их ребро (дуга), тогда вершина 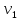и ребро 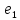инцидентны, вершина 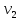и ребро 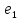тоже инцидентны. Две вершины или два ребра (дуги) инцидентными быть не могут. Понятие инцидентности для орграфов сохраняется (то есть начальная или конечная вершина — не имеет значение), но различается в особых случаях — положительная инцидентность (дуга исходит из вершины) и отрицательная инцидентность (дуга заходит в вершину).

Изоморфизм двух графов — понятие, используемое в случае, если существует перестановка вершин, при которой два графа совпадают. Иначе говоря, два графа называются изоморфными, если существует взаимно-однозначное соответствие между их вершинами и рёбрами, которое сохраняет смежность и инцидентность (то есть графы отличаются только названиями своих вершин). В случае матрицы смежности: графы являются изоморфными, если путём перестановки строк и столбцов матрицы смежности первого графа удаётся получить матрицу смежности второго графа.

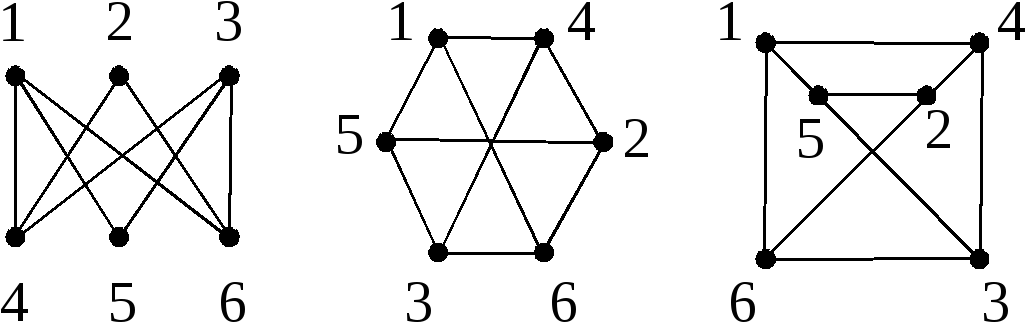
Рисунок 1. Все три графа — изоморфны

Порядок графа — число вершин в графе: .

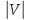Размер графа — число рёбер (дуг) в графе: .

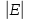Степень 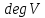вершины 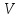— количество инцидентных ей рёбер (при этом петли считают дважды).

Изолированная вершина — вершина, которая не является концом ни одного ребра.

Висячая вершина (или лист) — вершина, которая является концом ровно одного ребра.

Путь — конечная последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершиной ребром или дугой. Длина пути — число составляющих его рёбер и дуг.

Простой путь — путь, в котором рёбра (дуги) не повторяются.

Элементарный путь — простой путь, в котором вершины не повторяются.

Цикл — путь, в котором первая и последняя вершины совпадают. Длина цикла — число составляющих его рёбер и дуг.

Простой цикл (или контур) — цикл, в котором только первая и последняя вершины совпадают, а все остальные — нет.

Цепь (или маршрут) — путь без повторяющихся рёбер.

Простая цепь (или простой маршрут) — цепь без повторяющихся вершин.

Расстояние между вершинами — минимальная длина пути, который соединяет эти вершины.

Связность означает наличие пути между любой парой вершин.

Бинарное отношение на множестве вершин графа, заданное как «существует путь из в 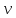», является отношением эквивалентности и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный.

Компонента связности графа — всякий максимальный связный подграф не орграфа. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов.

Рисунок 2. Граф с тремя компонентами связности

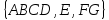
Мост (перешеек) — ребро графа, удаление которого увеличивает число компонент связности. (На рисунке выше все рёбра — мосты.)

Гамильтонов маршрут — простой маршрут в графе, содержащий все вершины графа ровно по одному разу.

Гамильтонов цикл — простой цикл в графе, содержащий все вершины графа ровно по одному разу (кроме первой, естественно).

На следующем рисунке последовательности вершин: 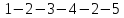— маршрут, 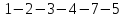и 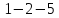— простые пути, 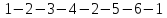— цикл (но не контур), 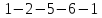— простой цикл (контур).

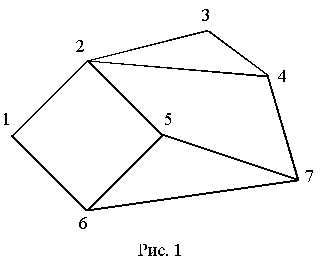
Рисунок 3