Оглавление

1. Основная задача электротехники. Основные понятия (эл. цепь, схема цепи, элементы цепи, ветви, узлы, контуры). Процессы, происходящие в цепях. Принципы наложения и взаимности. Их описание с помощью уравнений. 2

2. Источники и потребители энергии в цепи (активные и пассивные двухполюсники). Баланс мощности. 3

3. Основные законы и уравнения цепей с сосредоточенными параметрами. 4

4. Цепи постоянного тока. Особенности. 8

5. Расчёт цепей постоянного тока (последовательное, параллельное, смешанное соединение, соединение «звезда» и «треугольник») 9

6. Метод сворачивания 10

7. Метод уравнений Кирхгофа. 10

8. МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ 11

9. МЕТОД КОНТУРНЫХ ТОКОВ. 13

10. Метод эквивалентного генератора 14

11. Установившийся режим в цепи с последовательным соединением R, L и С 15

12. Установившийся режим в цепи с параллельным соединением R, L и С 17

13. Активная, реактивная и полная мощность Мгновенная мощность цепи синусоидального тока. Баланс мощности Мгновенная мощность – это произведение мгновенного значения напряжения и тока: 19

где 20

15. Основы комплексного метода расчета цепей синусоидального тока 22

1. Основная задача электротехники. Основные понятия (эл. цепь, схема цепи, элементы цепи, ветви, узлы, контуры). Процессы, происходящие в цепях. Принципы наложения и взаимности. Их описание с помощью уравнений.

   Основные задачи в области электротехники:

1. Расчеты и анализы цепей, т.е. определение связи между токами, напряжениями, параметрами заданной цепи и теми величинами, которые определяют работу рассматриваемой установки (например: к.п.д., падение напряжения, величина тока к.з. и т.д.). Также сюда входят и задачи математического описания цепей (геометрия и топология цепей, их матрицы); методы решения и анализа систем уравнений электрических цепей.

2. Принцип работы и общие свойства важнейших электротехнических устройств и элементов электрической цепи. Например, вопрос о согласовании приемника к источникам питания для получения максимальной мощности; теория резонанса.

3. Синтез электрических цепей.

Задачи синтеза заключаются в разработке методов такого выбора схемы соединения элементов цепи и такого подбора параметров этих элементов, чтобы полученная цепь обладала заданными характеристиками. Например, такой простой вопрос, как выбор параметров треугольника, эквивалентного заданной звезде, по существу относится к задаче синтеза.

4. Оптимизация электрических цепей. В том числе параметрическая оптимизация, т.е. выбор таких параметров цепи, которые соответствуют достижению целевой функции.

Электрическая цепь – совокупность устройств, предназначенных для прохождения в них электрического тока, электромагнитные процессы в которой могут быть описаны с помощью понятий: ток, напряжение (разность потенциалов), электродвижущая сила, заряд, магнитный поток, сопротивление, индуктивность, взаимная индуктивность и емкость.

Чтобы задать эл. цепь, нужно знать

1. из каких элементов (устройств) она состоит;

2. и как эти элементы друг с другом соединяются (топологию цепи).

Для линейных электрических цепей справедлив принцип наложения, согласно которому ток (напряжение) любой ветви равен сумме частичных токов (напряжений), создаваемых в этой ветви каждым из источников в отдельности. Этот принцип лежит в основе метода наложения. Метод наложения применим только для расчета линейных цепей.

Частичный ток – ток в ветви от действия только одного источника энергии, когда все остальные источники приняты нулевыми. Пусть в цепи действуют nидеальных источников ЭДС и m идеальных источников тока. Тогда ток в i-ой ветви может быть определен как

2. Источники и потребители энергии в цепи (активные и пассивные двухполюсники). Баланс мощности.

Пассивные элементы (потребители энергии)
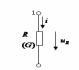
Резистор/активное сопротивление R		.
Индуктивная катушка/индуктивность L		,
Конденсатор/емкость C		,
NB В Если R, L, C – величины постоянные, то эти элементы называются линейными. Если цепь состоит из одних линейных элементов, то она считается линейной
Активные элементы (источники энергии)
Источник ЭДС (напряжения) e, E
Идеальный		u=
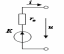
Реальный
Источник тока, J
Идеальный			i=J
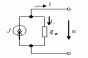
Реальный
NB идеальные источники не могут быть эквивалентно преобразованы друг в друга. Используются формулы перехода: ,

3. Основные законы и уравнения цепей с сосредоточенными параметрами.

Цепи, содержащие источники энергии, резисторы, индуктивные катушки и конденсаторы, могут быть представлены схемами замещения, состоящими из источников э.д.с., тока и элементов r, L, С. В схеме с сосредоточенными параметрами необратимые потери энергии происходят только в сопротивлениях, магнитное поле связано только с индуктивностями, ток смещения, обусловленный изменяющимся электрическим полем, имеет место только в емкостях.

Основные уравнения для цепей с сосредоточенными параметрами вытекают из известных физических законов — принципа непрерывности полного тока и закона электромагнитной индукции.

Из принципа непрерывности полного тока следует:

(1.12)

где i_k — ток k-го проводника, присоединенного к рассматриваемому узлу.

Уравнение (1.12) называют первым законом Кирхгофа, который формулируется следующим образом: алгебраическая сумма токов ветвей, соединенных в узле, равна нулю в любой момент времени. При этом с положительным (отрицательным) знаком учитывают токи, направленные от узла (к узлу).

Для узла на рис. 1.17 уравнение по первому закону Кирхгофа записывается следующим образом:

i₁-i₂+i₃-i₄=0.

Если в уравнении (1.12) токи источников тока перенести в правую часть, то получается

, (1.13)

где   — алгебраическая сумма токов источников тока;   — алгебраическая сумма токов других ветвей (элементов). В уравнении (1.13) с положительным (отрицательным) знаком записывают ток источника J_k, направленный к узлу (от узла), и ток i_k, направленный от узла (к узлу).

Например, если ток i₄ представляет собой ток источника тока, т. е. i₄=J₄ (рис. 1.17), то в соответствии с равенством (1.13)

i₁-i₂+i₃=J₄.

Из закона электромагнитной индукции следует:

(1.16)

Уравнение (1.16) называют вторым законом Кирхгофа, который формулируется следующим образом: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю в любой момент времени. При этом с положительным (отрицательным) знаком учитывают напряжения, положительные направления которых совпадают (противоположны) направлению обхода контура.

На рис. 1.18 показан пример контура цепи; путь интегрирования 1-а-2-3-б-4-1 содержит зажимы элементов. Для выбранного пути интеграл в равенстве (1.15) разбивается на четыре слагаемых:

-u₁+u₂-u₃+u₄=0,

где

u₁=₂-₁; u₂=₂-₃; u₃=₄-₃; u₄=₄-₁.

Если напряжения источников перенести в правую часть равенства (1.16) и заменить на э. д. с., то второму закону Кирхгофа соответствует уравнение

, (1.17)

которое выражает равенство алгебраических сумм напряжений на пассивных элементах и э. д. с. контура. В уравнении (1.17) с положительным (отрицательным) знаком записывают напряжения и э. д. с., направление которых совпадает (противоположно) с направлением обхода контура.

Например, для контура на рис. 1.18 по второму закону Кирхгофа записывают (выбирая направление обхода по часовой стрелке совпадающим с направлением э. д. с. e₁)

u₂-u₃+u₄=e₁

Уравнения (1.12), (1.16) или (1.13) и (1.17) совместно с соотношениями (1.3), (1.4), (1.6), (1.7), (1.9), (1.10), связывающими напряжения и токи каждого элемента, дают полное математическое описание цепи.

Пример 1.1. Составить уравнения Кирхгофа для схемы на рис. 1.19.

Решение. Для узлов 1 и 2, по первому закону Кирхгофа,

-i₁-i₂+i₃=J;

i₁+i₂-i₃=-J.

Одно из записанных уравнений является зависимым.

Для контура е₁ — r₁ — С — L₁ (при направлении обхода контура по часовой стрелке), по второму закону Кирхгофа,

.

Положительные направления напряжений на зажимах пассивных элементов приняты совпадающими с положительными направлениями токов и учтены выражения (1.3), (1.10), (1.6). Для контура С — r₂ —е₂ (направление обхода по часовой стрелке)

.

Для контура е₁ — r₁ — r₂ — е₂ — L₁ (направление обхода по часовой стрелке)

.

Последнее уравнение, записанное по второму закону Кирхгофа, равно сумме двух предыдущих уравнений.

Таким образом, из пяти уравнений Кирхгофа для схемы на рис. 1.19 независимыми являются три уравнения (одно для какого-либо узла и два других для любых двух контуров схемы).
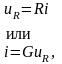
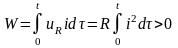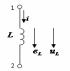
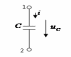
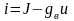
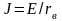