МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ЭКОНОМИКИ И ТОРГОВЛИ
им. М. ТУГАН-БАРАНОВСКОГО
КАФЕДРА ВЫСШЕЙ И ПРИКЛАДНОЙ МАТЕМАТИКИ
Э К О Н О М Е Т Р И Я
Учебное пособие
Утверждено на заседании кафедры высшей и прикладной математики.
Протокол № от 2002 г.
Одобрено учебно-методическим советом университета.
протокол № от 2002 г.
ДОНЕЦК 2002
УДК 330. 115
Эконометрия. Учебное пособие. /Cост. Пенина Г.Г., Шепеленко О.В., Узбек Е.К., Орлова Л.М. - Донецк: ДонГУЭТ, 2002. - 79 с.
Учебное пособие предназначено для студентов дневного и заочного отделений экономических специальностей. Его цель – помочь студентам усвоить темы курса эконометрии. Учебное пособие содержит теоретические вопросы, а также решения типовых задач. Даны рекомендации к решению задач, которые предназначены в помощь студентам при выполнении контрольной работы.
Рецензент: Винда Е.В., канд. техн. наук, доцент
© Донецкий государственный университет
экономики и торговли
им. М.Туган-Барановского, 2002
Вступление
Эконометрия – это наука, изучающая количественные закономерности и взаимозависимости экономических процессов и объектов с помощью математико-статистических методов и моделей.
Возрастающей интерес к эконометрии вызван современным этапом развития экономики в государстве, формированием рыночных отношений. Эконометрия имеет инструментарий, который позволяет перейти от качественного уровня анализа к уровню, который использует количественные статистические значения исследуемых величин. Она рассматривает не отдельные частичные характеристики, а строится на комплексном исследовании всего экономического процесса.
Эконометрия является синтезной дисциплиной; она объединяет в себе экономическую теорию, математическую экономику, экономическую и математическую статистику. Курс эконометрии тесно связан с микроэкономикой, макроэкономикой, финансовым анализом, обеспечивая прикладные знания специалистов. В нем содержатся исследовательские приемы изучения взаимосвязи экономических явлений, выдвигаются и проверяются гипотезы о наличии корреляционных связей между признаками, количественно оценивается существенность взаимосвязей, определяются формы связи и проводится выбор уравнений, оценивается достоверность параметров, строятся однофакторные и многофакторные регрессионные модели, дается оценка их адекватности и надежности.
Особое место занимает исследование связи в динамических процессах путем построения авторегрессионных моделей и оценки возможности использования их в прогнозировании. Без эконометрических методов нельзя построить надежного прогноза, а значит – под вопросом и успех в управлении экономическими процессами в бизнесе, банковском деле, финансах.
1 Модели рядов динамики
Одной из важнейших задач исследования экономических процессов является изучение изменения экономических показателей с течением времени (товарооборота, объема выпуска продукции, производительности труда и т.д.). Эта задача решается с помощью упорядочения и анализа рядов динамики.
Динамическим рядом называется последовательность результатов наблюдений за явлением через равные промежутки времени.
Изучая ряды динамики, стремятся обнаружить основную, главную тенденцию в изменении показателей ряда. Аналитическое моделирование рядов динамики проводится с помощью простейших экономико-математических моделей: линейной, параболической, гиперболической, логарифмической, показательной, степенной и других.
Пример 1.
Проанализировать показатели реализации мучных изделий в государственной торговле Донецкой области за ряд лет. Найти уравнения линейной, параболической и гиперболической зависимостей. Проверить адекватность полученных экономико-математических моделей, определить наилучшую модель.
Годы |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
Реализация изделий, тыс.т |
12,1 |
12,9 |
13,7 |
13,9 |
14,5 |
15,1 |
15,7 |
16,1 |
16,6 |
17,1 |
Решение. Данные таблицы показывают, что реализация продукции неуклонно возрастала, хотя происходило это неравномерно. Очевидно, существует ряд факторов, под влиянием которых изменяется величина объема реализации. Некоторые из факторов могут действовать долгосрочно, а другие – кратковременно; некоторые могут быть важными, другие – случайными.
Для выравнивания показателя реализации мучных изделий в государственной торговле будем использовать такие функции: линейную, параболическую и гиперболическую. Параметры избранных для моделирования функций можно найти с помощью метода наименьших квадратов. На его основе для каждой из функций формируют специальную систему уравнений Гаусса. Для указанных функций приведем соответствующие системы:
Линейная
-
|
(1) |
Параболическая
-
|
(2) |
Гиперболическая
-
|
(3) |
В
любой из систем (1)-(3)
– результативный показатель;
– фактор времени;
– количество наблюдений;
– параметры моделей.
Отсчет временного показателя начинают от 1. Составим вспомогательную расчетную таблицу 1 и на ее основе сформируем системы Гаусса.
Таблица 1 - Вспомогательные расчеты для формирования систем Гаусса
х |
у |
x2 |
x3 |
x4 |
уx |
yx2 |
1/x |
1/x2 |
y/x |
1 |
12,1 |
1 |
1 |
1 |
12,1 |
12,1 |
1 |
1 |
12,1 |
2 |
12,9 |
4 |
8 |
16 |
25,8 |
51,6 |
0,5 |
0,25 |
6,45 |
3 |
13,7 |
9 |
27 |
81 |
41,1 |
123,3 |
0,333 |
0,111 |
4,5667 |
4 |
13,9 |
16 |
64 |
256 |
55,6 |
222,4 |
0,25 |
0,0625 |
3,475 |
5 |
14,5 |
25 |
125 |
625 |
72,5 |
362,5 |
0,2 |
0,04 |
2,9 |
6 |
15,1 |
36 |
216 |
1296 |
90,6 |
543,6 |
0,167 |
0,0278 |
2,5167 |
7 |
15,7 |
49 |
343 |
2401 |
109,9 |
769,3 |
0,1428 |
0,0204 |
2,2429 |
8 |
16,1 |
64 |
512 |
4096 |
128,8 |
1030,4 |
0,125 |
0,0156 |
2,0125 |
9 |
16,6 |
81 |
729 |
6561 |
149,4 |
1344,6 |
0,111 |
0,0123 |
1,844 |
10 |
17,1 |
100 |
1000 |
10000 |
171 |
1710 |
0,1 |
0,01 |
1,71 |
55 |
147,7 |
385 |
3025 |
25333 |
856,8 |
6169,8 |
2,9288 |
1,5496 |
39,8178 |
В последней строке таблицы 1 указаны суммы всех значений для каждого столбца.
Составим системы для трех функций и найдем соответствующие уравнения.
Для определения параметров уравнения линейной функции запишем систему уравнений (1) и найдем ее решение:
Таким
образом,
– линейная модель.
Для определения параметров уравнения параболической функции запишем систему уравнений (2) и найдем ее решение с помощью метода Гаусса:
Таким
образом,
– параболическая модель.
Для определения параметров уравнения гиперболической функции запишем систему уравнений (3) и найдем ее решение
Таким
образом,
– гиперболическая модель.
Адекватность экономико-математической модели может быть установлена с помощью средней ошибки аппроксимации (среднего процента расхождения теоретических и фактических значений):
,
(4)
где
–
фактические значения показателя,
– теоретические значения, найденные
по уравнению.
Для
этого по каждому уравнению находят
теоретические значения
,
подставляя в него соответствующие
значения
,
и для каждого значения
рассчитывают
,
потом находят среднее значение
.
При
моделировании экономических показателей
чаще всего допускается 5% погрешность
(иногда 7%, редко 10%). Модель считается
адекватной (то есть пригодной), если
.
Выбор наилучшей модели можно проводить на основе остаточного среднеквадратичного отклонения (остаточной дисперсии):
,
(5)
где
–
количество параметров в уравнении.
Лучшей
будет та функция, для которой значение
меньше.
Таблица 2 - Расчеты для линейной функции
-
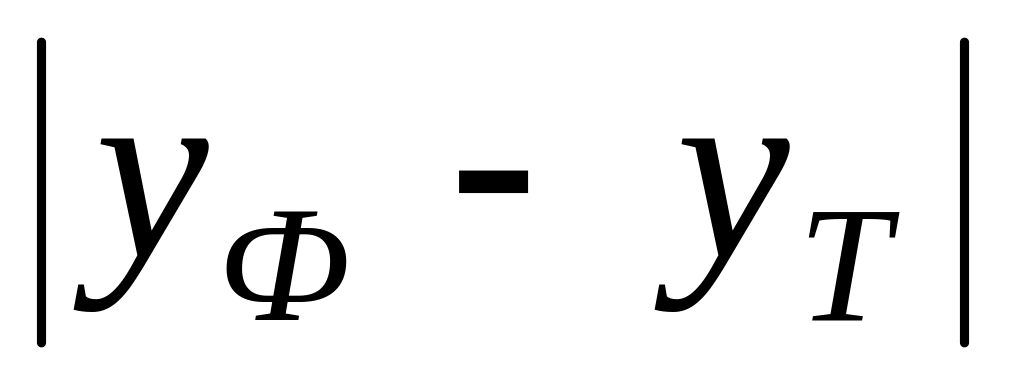
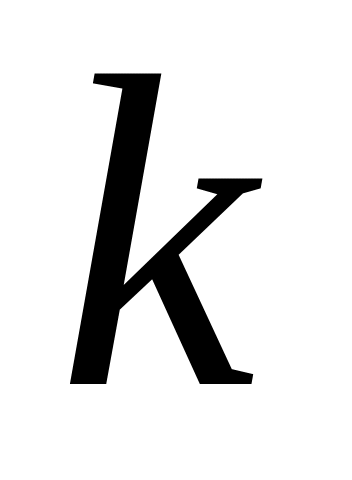
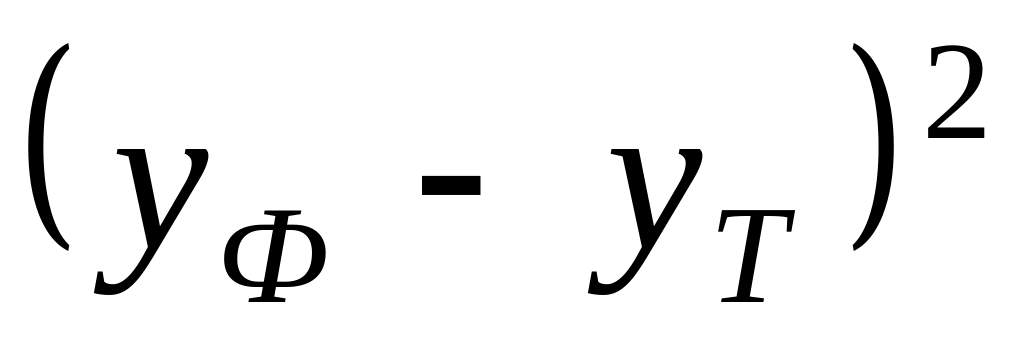
1
12,1
12,3458
0,2458
1,991
0,060418
2
12,9
12,8846
0,0154
0,1195
0,000237
3
13,7
13,4234
0,2766
2,0606
0,076508
4
13,9
13,9622
0,0622
0,4455
0,003869
5
14,5
14,501
0,001
0,0069
0,000006
6
15,1
15,0398
0,0602
0,4003
0,003624
7
15,7
15,5786
0,1214
0,7793
0,014738
8
16,1
16,1174
0,0174
0,1079
0,000303
9
16,6
16,6562
0,0562
0,3374
0,003158
10
17,1
17,195
0,095
0,5525
0,009025
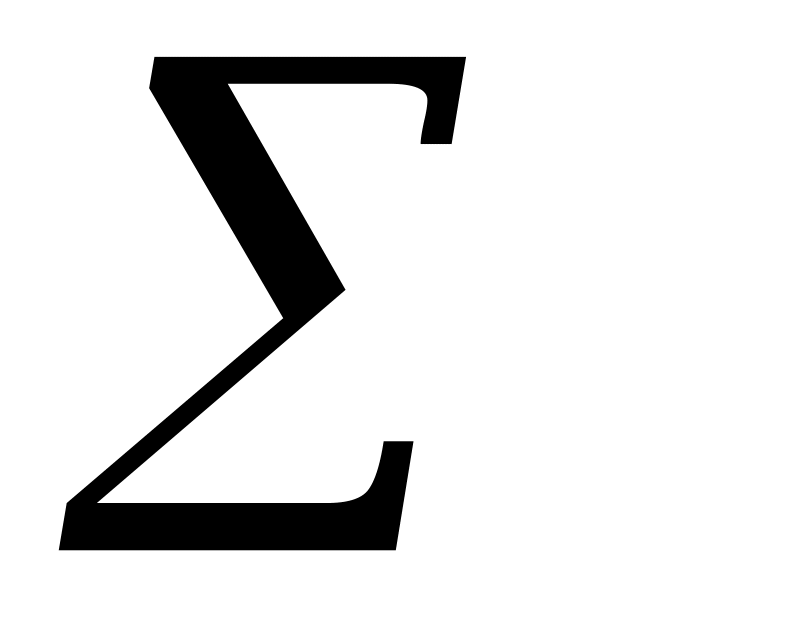
6,8008
0,17188
Из
формул (4), (5) имеем:
;
.
Таблица 3 - Расчеты для параболической функции
-
1
12,1
12,2251
0,1251
1,023305
0,01565
2
12,9
12,8445
0,0555
0,432092
0,00308
3
13,7
13,4437
0,2563
1,906469
0,06569
4
13,9
14,0227
0,1227
0,87501
0,015055
5
14,5
14,5815
0,0815
0,558927
0,006642
6
15,1
15,1201
0,0201
0,132936
0,000404
7
15,7
15,6385
0,0615
0,39326
0,003782
8
16,1
16,1367
0,0367
0,227432
0,001347
9
16,6
16,6147
0,0147
0,088476
0,000216
10
17,1
17,0725
0,0275
0,161078
0,000756
5,798984
0,112623
Из
формул (4), (5) имеем:
;
.
Таблица 4 - Расчеты для гиперболической функции
-
1
12,1
11,251
0,8489
7,5450
0,7206
2
12,9
13,739
0,83905
6,1070
0,7040
3
13,7
14,568
0,868367
5,9606
0,7541
4
13,9
14,983
1,083025
7,2283
1,1729
5
14,5
15,232
0,73182
4,8045
0,5356
6
15,1
15,398
0,297683
1,9333
0,0886
7
15,7
15,517
0,183843
1,1848
0,0338
8
16,1
15,605
0,4945
3,1720
0,2450
9
16,6
15,674
0,9259
5,9070
0,8573
10
17,1
15,729
1,3706
8,71355
1,8785
52,556
6,9904
Из
формул (4), (5) имеем:
.
Поскольку
,
то
эта модель адекватной не является и
считать для нее
не надо.
Составим сводную таблицу для статистических оцениваемых характеристик:
Таблица 5 - Статистические оценки для исследуемых моделей
Вид функции |
|
|
Линейная |
0,68 |
0,147 |
Парабола |
0,579 |
0,127 |
Гипербола |
5,25 |
– |
Из
сравнения средних ошибок аппроксимации
видно, что для гиперболической функции
она выходит за 5% уровень, у линейной
модели и параболической эта характеристика
не выходит за 5% уровень и приблизительно
одинаковая. Если оценивать преимущество,
то очевидно, что лучшей есть параболическая
функция, поскольку у нее остаточное
среднеквадратичное отклонение
меньше всего.