7.2.4Формализм исследования операций

До сих пор мы изучали экономико-математические модели и соответствующий им математический аппарат, с помощью которого исследовались ситуации, не содержащие неизвестных факторов. Следовательно, стратегии оперирующей стороны состояли только из так называемых стратегий-констант.

Применяя формализм исследования операций в процессе принятия решения, оперирующая сторона выполняет определенную последовательность шагов. Рассмотрим с точки зрения ЛПР этапы контроля выбранных параметров и выбор управляющих воздействий.

Пусть — множество значений преобразования : , которое определяет совокупность всех значений контролируемых факторов.

Управляемо-контролируемыми факторами (УК-факторы) назовем компоненты вектора , где — интервал, на котором определены вектор-функции , . Естественно считать, что . Таким образом, ЛПР в процессе управления отслеживает (контролирует, измеряет) величины и, если это необходимо, определяет величины , ,  как решение некоторой обратной задачи управления, например задачи синтеза оптимального управления.

Выбор УК-факторов зависит от целей и условий проведения операции.

Ряд факторов формируются независимо от оперирующей стороны и являются неуправляемыми.

Неуправляемые факторы, к которым, в частности, относятся природные неопределенные факторы, группируются по степени информированности о них оперирующей стороны:

неопределенные факторы — вектор : оперирующей стороне известно лишь множество их значений ;

случайные факторы — вектор : оперирующей стороне известно множество значений случайной величины ; кроме того, известна некоторая информация о законе распределения (т.е. функция распределения или вероятностная мера) этой случайной величины: он может быть известен точно, либо известно лишь, что , где — множество законов распределения.

Условным решением называется точка множества , а само множество — множеством условных решений.

При существовании множества альтернативных вариантов достижения поставленной цели ЛПР формирует правило приоритета выбора условных решений: критерий эффективности операции — . Оперирующая сторона стремится выбрать УК-факторы так, чтобы максимизировать значение функции .

7.3Примеры принятия решений в присутствии неконтролируемых факторов

Рассмотрим ряд примеров.

7.3.1Модель производства продукции в условиях конкуренции

Вспомним Error: Reference source not found.

7.3.2Модель производства продукции в условиях конкуренции

Обобщая модель, описанную в п. Error: Reference source not found получим модель производства продукции в условиях конкуренции. Пусть имеется видов продукции, нумеруемых индексом , которые могут быть проданы на внешнем рынке по цене за единицу продукции. Внешний рынок, естественно, ограничен как по количеству продукции -го типа (спрос в натуральном выражении), так и по сумме денег (платежеспособный спрос), которую покупатели могут выделить на приобретение всех видов продукции за год.

Пусть производство вектора = продукции, состоящего из единиц -й продукции в год, требует расхода или наличия единиц производственных факторов (деньги, рабочая сила, оборудование и т.п.). Первый номер присвоим деньгам. Пусть вектор = описывает годовые запасы производственных факторов.

Предположим, наконец, что имеется конкурент, также могущий производить единиц -й продукции и продавать ее по цене ; будем считать, что .

Показатель эффективности операции выражает, естественно, стремление оперирующей стороны к увеличению прибыли, т.е.

70. = ,

где

71. ;

при этом должны быть выполнены условия

72. , ,

выражающие ограниченность использования производственных факторов.

Величины выражают информированность оперирующей стороны о возможных действиях потребителя -й продукции. Так, по ее мнению, будут приобретаться товары участника, назначающего меньшую цену.

Чтобы объяснить показатель эффективности, разложим его на 3 части:

• величина 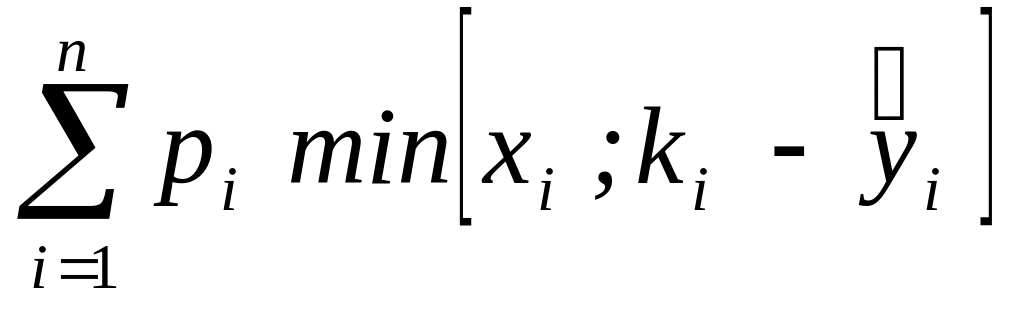выражает доход: возможность продажи произведенной продукции в условиях поступления на рынок также товаров конкурента (насыщение спроса в натуральном виде);

• величина отражает покупательную способность потребителя;

• величина отражает необходимые затраты на производство.

Если в такой задаче величины и считаются заданными, то стратегиями являются векторы = , а неопределенными факторами могут быть = , выбираемые конкурентом. В этом случае должны быть ограничены производственные возможности противника путем введения и лимитов , аналогичных и .

Стратегиями оперирующей стороны и конкурента могут стать и векторы и . Последнее особенно вероятно, если целью конкурента окажется уменьшение дохода оперирующей стороны.

В обычном же случае цель конкурента может быть записана совершенно так же, как цель оперирующей стороны.