2.4 Резонанс в электрических цепях переменного тока

Резонансом называется явление, возникающее в электрической цепи, содержащей индуктивные и емкостные элементы.

При резонансе векторы входного напряжения и тока совпадают по фазе , эквивалентное реактивное сопротивление или проводимость этой цепи равны нулю. Цепь в целом ведет себя как активный приемник, реактивная мощность при этом равна нулю.

Различают резонанс при последовательном соединении элементов R, L, C (см. рис. 25) – резонанс напряжений и резонанс при параллельном соединении элементов (см. рис. 27) – резонанс токов.

Резонанс напряжений (см. рис. 25). Явление данного резонанса характеризуется следующим условием:

т.е. (45)

или

(46)

Из условия (46) резонансная частота цепи

(47)

При резонансе реактивные сопротивления и не зависят от частоты, при которой это явление наступило, а определяются параметрами всей цепи:

(48)

– резонансное или волновое сопротивление цепи.

Векторно-топографическая диаграмма для случая резонанса напряжений в цепи приведена на рис. 48.

Рис. 48

Рассмотрим, какими явлениями характеризуется резонанс напряжений:

1. , тогда , следовательно, ток в режиме резонанса максимален, так как .

2. Векторы тока и напряжения совпадают по фазе, следовательно

3. Если , то

4. Напряжения на реактивных элементах , могут в несколько раз превышать приложенное к цепи напряжение U, если , поэтому внезапное возникновение режима резонанса в цепях большой мощности может вызвать аварийную ситуацию и привести к пробою изоляции.

,

где – затухание цепи.

Если , то согласно условию в режиме резонанса будут наблюдаться повышенные по сравнению со входным напряжения на реактивных элементах и .

Величина, показывающая, во сколько раз напряжение на реактивных элементах превышает напряжение на входе схемы, называется добротностью контура и определяется по формуле

5) Энергия электрического поля

Энергия магнитного поля

В режиме резонанса энергия электрического поля равна энергии магнитного поля, т.е.

Следует отметить, что в те моменты времени, когда энергия запасается в магнитном поле индуктивности, этот процесс осуществляется за счёт энергии электрического поля емкости. В следующий момент времени имеет место обратный переход энергии из магнитного поля в электрическое. Такие взаимопереходы отмечаются каждые четверть периода. Следовательно, при резонансе обмен реактивной энергией между внешним источником и приемником не происходит.

Резонанс токов (см. рис. 27) Явление характеризуется условием

, т.е.

или

Реактивные проводимости в режиме резонанса токов также не зависят от частоты.

,

где – резонансная или волновая проводимость цепи.

Векторная диаграмма для случая резонанса токов в цепи (см. рис. 27) приведена на рис. 49.

Рис. 49

Основные признаки резонанса токов:

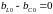1. , тогда , следовательно, ток в режиме резонанса токов минимален, так как

2. Векторы тока и напряжения совпадают по фазе, следовательно .

3. Если , то

4. Токи через реактивные элементы могут в несколько раз превышать ток в неразветвленной части цепи при условии .

,

где – затухание цепи.

Величина – добротность контура.

5. В цепи с параллельным соединением участков энергетические процессы при резонансе аналогичны энергетическим процессам в цепи с последовательным соединением элементов . Следовательно, обмен энергией между внешним источником и приемником не происходит.

Примеры решения задач

Пример 1

Рассчитать все характеристики схемы (рис. 50) построить векторную диаграмму при резонансе напряжений.

Рис. 50

Дано:

U = 100 В;

R = 100 Ом;

L = 2 Гн;

С = 8 мкФ.

Решение

Резонансная частота

Волновое сопротивление

_{Затухание}

_{Добротность}

_{Значение тока}

_{Напряжения на элементах:}

_{Построим векторную диаграмму (рис. 51).}

_{Рис. 51}

Пример 2

Найти емкость, при которой в схеме будет наблюдаться резонанс напряжений (рис. 52).

Рис. 52

Дано:

U = 200 В;

R = 10 Ом;

X_L = 5 Ом;

f = 50 Гц.

Определить ток, потребляемый схемой.

Решение

Условие резонанса или

Емкостное сопротивление

Величина емкости при резонансе

, следовательно,

Так как , то ток в режиме резонанса

Пример 3

Рис. 53

Найти емкость, при которой в схеме будет наблюдаться резонанс напряжений (рис. 53).

Дано:

U = 200 В;

R = 10 Ом;

Х_L = 5 Ом;

f = 50 Гц.

Определить ток, потребляемый схемой.

Решение

Условие резонанса или

Полное сопротивление схемы

При резонансе реактивная часть полного сопротивления равна нулю, т.е.

или

Подставив в данное выражение значение R, получим

.

Решая квадратное уравнение, получим

, следовательно,

Активное сопротивление схемы – это действительная часть комплекса полного сопротивления

Ток в режиме резонанса

Мощность схемы

Пример 4

Рис. 54

Рассчитать все характеристики схемы при резонансе токов (рис. 54).

Дано:

U = 100 В;

R = 10 Ом;

L = 4 МГн;

С = 10 мкФ.

Решение

Резонансная частота

Волновая проводимость

\

_{Затухание}

_{Добротность}

_{Полная проводимость схемы}

_Токи:

_{Мощность}

_{Построим векторную диаграмму (рис. 55).}

Рис. 55