
Mensch und Fahrzeug
.pdf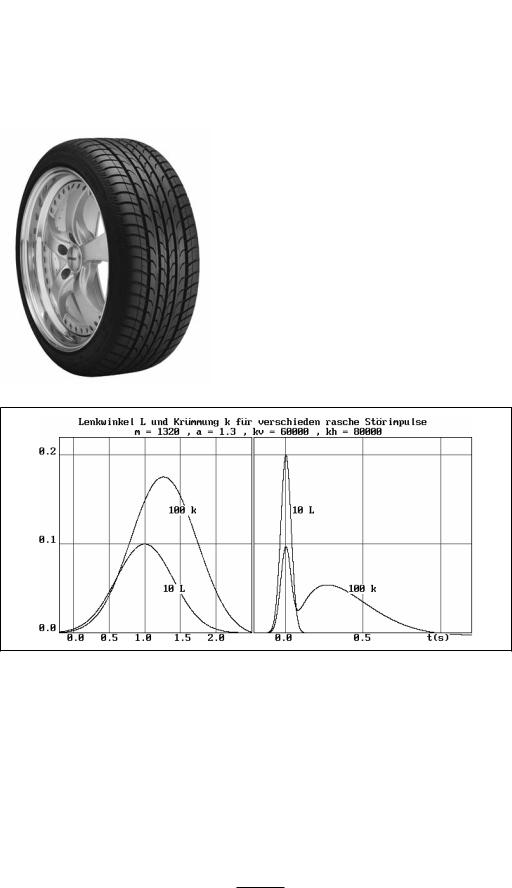
114 |
3 Lenken – Fahrzeugführung quer |
Die Anforderungen an das Lenkverhalten moderner Pkw’s steigen ständig, so dass auch indirekte Lenksysteme diskutiert werden, siehe Beispiel 6.
Beispiel 6 Lenkverhalten:
Hochleistungsreifen mit guten Bremseigenschaften auf nassen Fahrbahnen bei gleichzeitig gutem Handling sowie geringer Geräuschentwicklung (Werkbild Fulda)
Bild 3-24 Antwort der Fahrspurkrümmung k auf eine verschieden rasche Eingabe des Lenkwinkels L. Wird der Lenkimpuls innerhalb von 2 s aufgebracht (was normalem Fahrbetrieb entspricht), dann folgt das Fahrzeug mit einer Verzögerung von etwa 0.25 s. Dauert der Lenkimpuls nur 0.2 s (rechts), dann folgt die Krümmung mit geringer Verzögerung um nach etwa 0.25 s ein zweites Maximum zu erreichen.
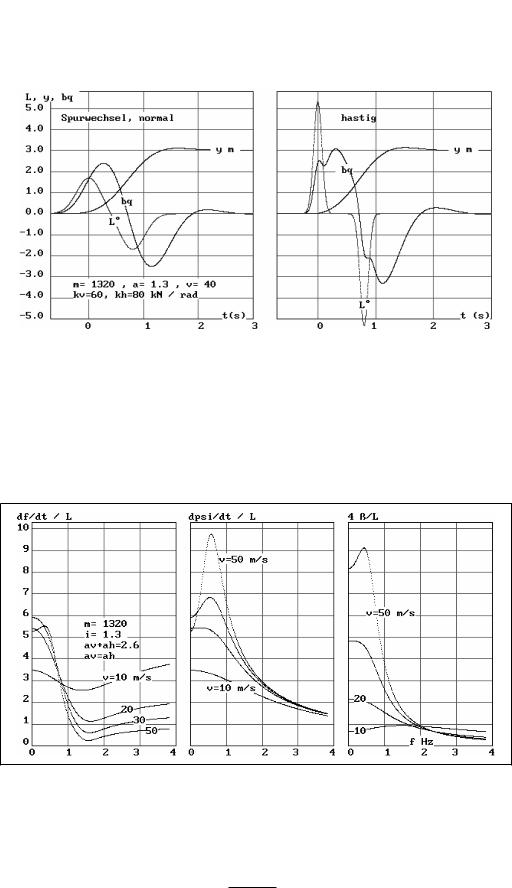
Ein Spurwechsel ist in Bild 3-25 untersucht. Die Lenkung wird nach zwei aufeinander folgenden Glockenkurven verstellt, so dass sich im linken und rechten Bild der gleiche Spurwechsel y einstellt. Bei der sanften (normalen) L-Verstellung (links) folgt das Fahrzeug harmonisch, bei der raschen Verstellung aber hektisch. Der unruhige Verlauf der Querbeschleunigung in diesem Fall wird von Fahrer und Insassen als beunruhigend empfunden.
|
3.2 Reales Fahrzeug, Fahrdynamik |
115 |
|
|
|
|
|
|
Bild 3-25 Wie 3-24, aber für verschieden raschen Lenkimpulse zum Spurwechsel.
Eine Untersuchung des Frequenzganges zeigen die Bilder 3-26 bis 3-29. Dabei wird der Lenkwinkel L mit fe Hz verstellt. Bei f = 0 stellt sich je nach Fahrgeschwindigkeit v der stationäre Wert ein. In der Nähe der Kennfrequenz des Fahrzeuges (etwa 0.5 Hz) kommt es aber zu einer Überhöhung. Bild 3-29 zeigt den Vergleich mit einer praktischen Untersuchung, wobei die Annahmen so verändert wurden, dass sich ein ähnlicher Verlauf der Antwortkurven ergibt.
Bild 3-26 Frequenzgang den Schwimmwinkel ß und für die Geschwindigkeit des Richtungswinkels f, des Gierwinkels psi. Erregung L. L = EXP(w · t) = COS (w · t) + i SIN (w · t) (w = 2 pi, fe, fe.. Erregerfrequenz) für verschiedene Fahrgeschwindigkeiten v.
116 |
3 Lenken – Fahrzeugführung quer |
|
|
|
|
|
|
|
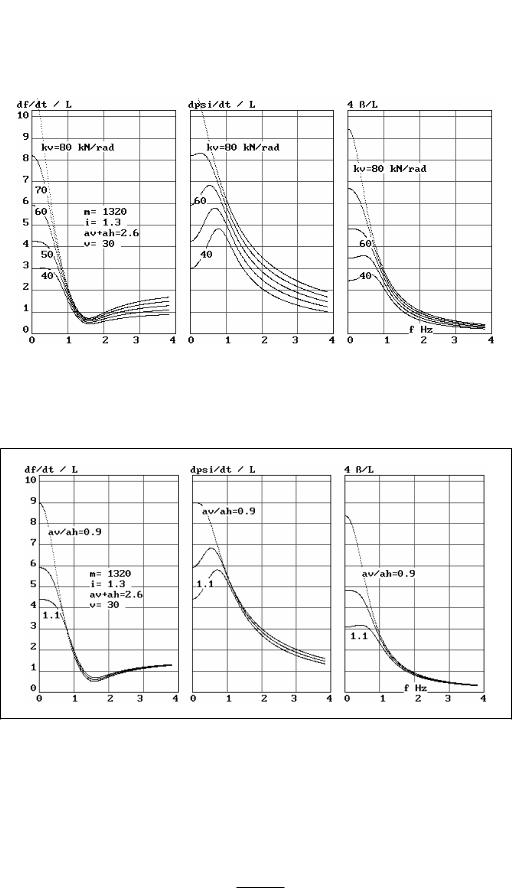
Bild 3-27 Wie 3-26, aber Variation des Seitenkraftbeiwerts vorn kv
Bild 3-28 Wie 3-26, aber Variation der Schwerpunktlage (av/ah)
|
3.3 Reifen und Lenkmoment |
117 |
|
|
|
|
|
|
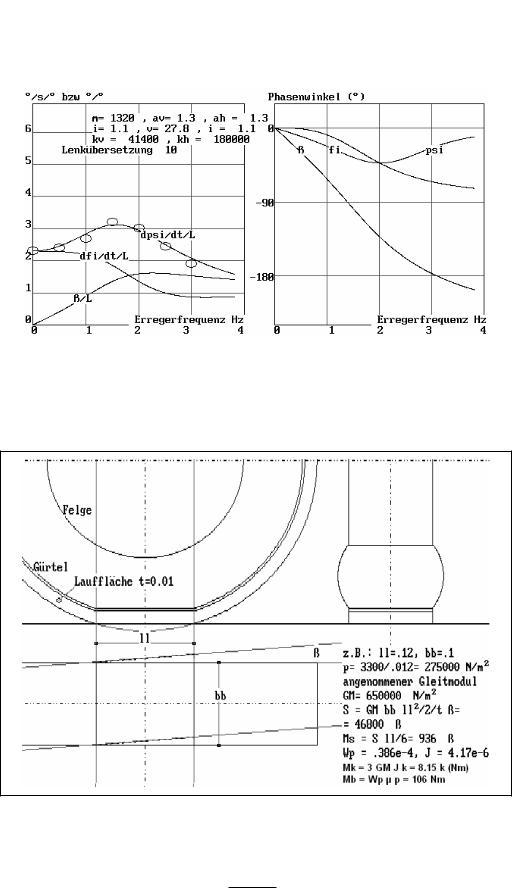
Bild 3-29 Frequenzgang und Phasenwinkel, Messwerte im Vergleich zu Rechenwerten >3.20 .
3.3 Reifen und Lenkmoment
Bild 3-30 Vereinfachtes Reifenmodell.

118 |
3 Lenken – Fahrzeugführung quer |
Das einfachste Radmodell erzeugt durch seine Abplattung die Aufstandsfläche von der Länge ll und der Breite bb (dargestellt in Auf-, Grundund Kreuzriss). Auf ihr stützt sich die Radlast (hier mit 3300 N angenommen) ab mit einer Pressung von p = 27.5 N/cm2, was dem Radinnendruck + dem Druck zur Deformation des Reifens entspricht. Die Lauffläche hat eine Dicke von t. Rollt das Rad mit dem Schräglaufwinkel Ε, dann verformt sich die Lauffläche, so lange die Schubspannung kleiner als die örtliche Haftung µ · p ist, und erzeugt damit die Seitenkraft S, die im Schwerpunkt des Deformationsdreieck, also um ll/6 hinter der Mitte der Aufstandfläche angreift. Mit dem angegebenen Gleitmodul GM errechnet sich der Zusammenhang von S und Ms mit Ε (ο vergleiche Bild 3.3-1 und 3.3-7). – Bei einer Kurvenfahrt wird die Aufstandfläche gekrümmt, was zu einem Moment Mk = E · J · k führt (E = Elastizitätsmodul = 3 GM, J = Flächenträgheitsmoment der „Aufstandsfläche“, k = Krümmung der Fahrspur).
Wird das Rad im Stillstand um die Mitte der Aufstandfläche gedreht, dann entsteht das „Bohrmoment“ Mb = Wp · µ · p (Wp = polares Widerstandsmoment für plastische Verformung, weil fast alle Flächenelemente bis zur Haftgrenze µ · p zunehmen).
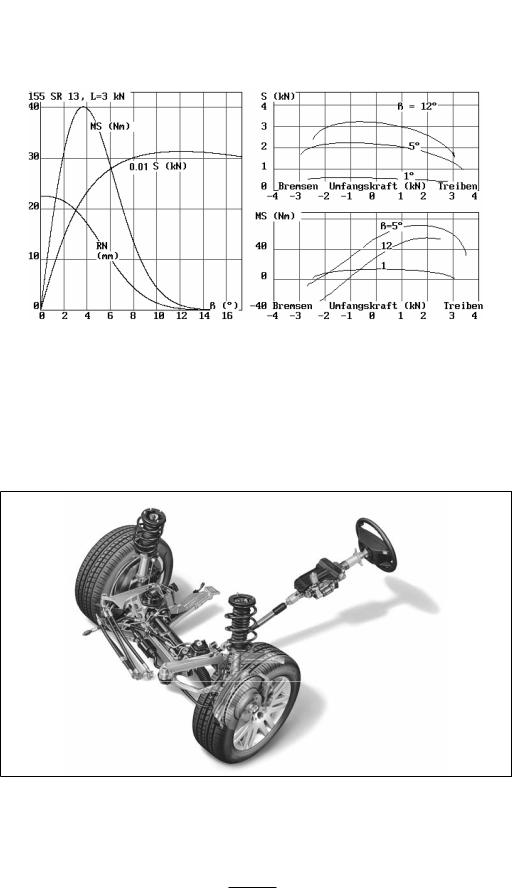
In Bild 3-30 sind die Kräfte und Momente am rollenden Reifen und deren Zustandekommen qualitativ erklärt. Es ist eine Aufstandfläche ll mal bb angenommen, auf die sich die Radlast gleichförmig verteilt. Für die dort genannten Annahmen ergibt sich ein gleicher Druck von p = 27.5 N/cm2. Das entspricht etwa dem Reifeninnendruck. Verschiebt sich die auf der Straße haftende Auflage gegen das Rad, dann entsteht eine Schubverformung der Lauffläche, die der angreifenden Kraft proportional ist. (Gleitmodul GM) Läuft der Reifen mit einem kleinen Winkel Ε schräg, dann verformt sich die Lauffläche über die Länge zunehmend. Die dabei entstehende Seitenkraft ist S = GM · bb · ll2/2 · Ε. Für einen Gleitmodul von 20 N/cm2 ist S = ki · Ε, wobei ki = 46800 der Seitenkraftbeiwert des Rades ist. Mit zunehmendem ß wird die Schubspannung die örtliche Haftung überschreiten, die Seitenkraft dann asymptotisch den Grenzwert von Radlast mal Haftbeiwert zustreben.
Die Seitenkraft greift für kleine Winkel Ε um a/6 hinter der Mitte der Aufstandsfläche an, rückt aber für größer werdende Ε immer näher an die Mitte der Aufstandfläche heran. Das Schräglaufmoment ist zunächst S · a/6, schließlich aber 0. Für Ε << 1 gilt M = 936 Ε · Nm.
Wird das stillstehende Rad um die Mitte der Aufstandfläche um den Winkel fi gedreht, dann entsteht das Moment
Mk = GM · Id / t · fi
Id polares Flächenträgheitsmoment
TDicke der Lauffläche, hier mit t = 1 cm angenommen
Rollt der Reifen, dann ist fi = a/R = a · k und das Kurvenmoment Mk = 4.8 k · Nm (k in 1/m). Wird das stillstehende Rad weiter gedreht, dann überschreitet die örtliche Schubspannung den Haftwert, das Moment
Mb = Wdp · µ · p
Wdp polares Widerstandmoment für „plastische Spannungsverteilung“
µder örtliche Haftbeiwert
Mit den angenommenen Zahlenwerten ist die Bohrreibung Mb = 106 Nm.
Auf die Achse bezogen, müsste für kleine Kurvenradien berücksichtigt werden, dass der Kurvenradius des kurveninneren Rades kleiner als der des Kurvenäußeren ist. Dieser Fehler wird im Folgenden akzeptiert.
|
3.3 Reifen und Lenkmoment |
119 |
|
|
|
|
|
|
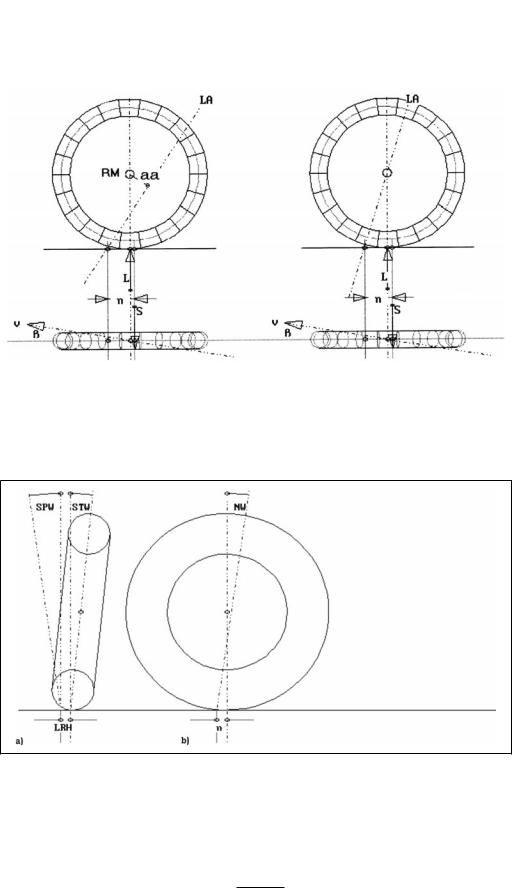
Bild 3-31 Momente um die Hochachse eines Einzelrades. Aus dem Nachlaufwinkel folgt das Moment Mi = Last n sin(NW) sin(L), aus der Krümmung der Spur das Moment Mk (links), die beide mit der Krümmung zunehmen. Rechts ist das gesamte Moment bestehend aus Mi, Mk und Ms, abhängig von der Rollgeschwindigkeit für die Querbeschleunigungen 1 – 4 m/s2, aufgetragen. Für Fahrgeschwindigkeiten über 10 m/s ist das Moment der Seitenkraft fast allein maßgebend.
Neuere Entwicklungen auf dem Reifensektor zeigen, dass die komplexen Anforderungen an heutige Reifen zu einer Fülle von Eigenschaften führen, Beispiel 7.
Beispiel 7 Lenkverhalten: Steigende Ansprüche an Agilität, Fahrkomfort, Fahrstabilität und strengere Restriktionen bezüglich des Kraftstoffverbrauchs erfordern neue Ansätze, wie vollständige Steer-by- Wire-Funktionalität (Werkbild BMW).
120 |
3 Lenken – Fahrzeugführung quer |
|
|
|
|
|
|
|
Bild 3-32 Lenkung beim Fahrrad (links) und Auto (rechts)
Bild 3-32a Stabilität um die Lenkachse

3.3 Reifen und Lenkmoment |
121 |
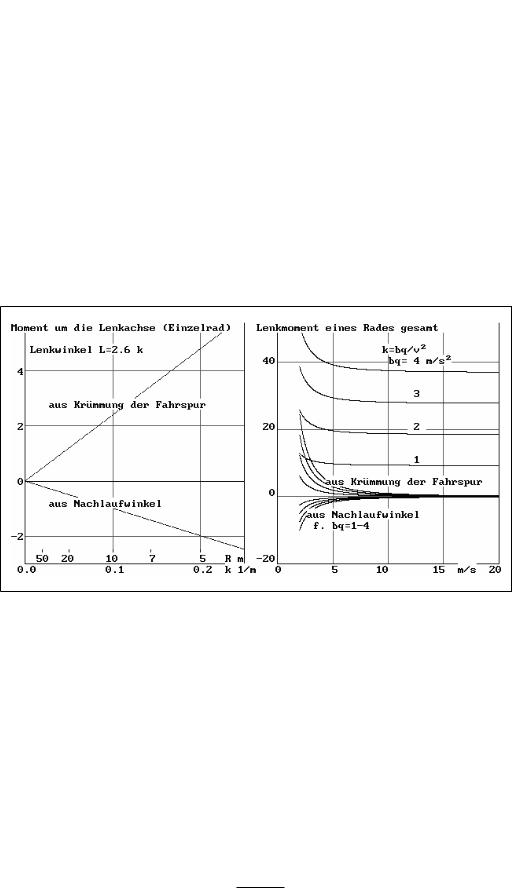
a) Bild 3-32: Lenkung bei Fahrrad (links) und Auto (rechts). Beim Fahrrad liegt der Schwerpunkt der Radmasse RM über der Lenkachse LA. Wenn man das Fahrzeug aus der Bildebene heraus bewegt, entsteht daraus und aus der Radlast ein Moment um die Lenkachse, das zu einem Linkseinschlag führt. Befindet sich das Fahrzeug in Fahrt, dann bewirken Seitenkraft S und ein rückdrehendes Moment Mk um die Lenkachse. Hält der Fahrer die Momente gleich groß, dann kann er freihändig fahren. Durch Neigen des Fahrrades in die Kurve kann er den Kurvenradius verkleinern und umgekehrt.
Beim zweispurigen Fahrzeug kann der Neigungswinkel nicht direkt beeinflusst werden. Der Schwerpunkt des Rades kann auf der Lenkachse liegen. Die Momente um die Lenkachse muss der Fahrer am Lenkrad aufbringen. Das Seitenkraftmoment sorgt für Fahrtrichtungsstabilität: bei losgelassener Lenkung fährt das Auto geradeaus so lange nicht Störungen wirken.
b) Bild 3-32a: Radstellung: Die Radebene ist gegen die Fahrbahnebene um den Sturzwinkel STW geneigt, die Lenkachse in Querrichtung um den Spreizwinkel SPW (links). Der Durchstoßpunkt der Lenkachse liegt um den Lenkrollhalbmesse LRH innerhalb. Durch STW und SPW kann der LRH beliebig gewählt werden.
In der Seitenansicht rechts ist die Lenkachse um den Nachlaufwinkel NW geneigt. Sie durchstößt die Fahrbahn um den Nachlauf n vor dem Aufstandpunkt des Rades.
Wie man sich durch Anheben eines Fahrrades leicht überzeugen kann, ist das Vorderrad instabil: es schlägt nach der einen oder anderen Seite ein, wenn man es ein wenig neigt. Das ist darauf zurückzuführen, dass der Schwerpunkt des Vorderrades über der Lenkachse liegt, Bild 3-32a. Wenn man das rollende Fahrrad am Sattel anfasst, kann man es durch entsprechendes Neigen stabil in die gewünschte Richtung führen: Linksneigung führt zur Linkskurve und umgekehrt. Mit zunehmender Geschwindigkeit tritt eine Seitenkraft auf, dessen Moment um die Lenkachse dem Neigungsmoment entgegengerichtet ist. Es ergibt sich ein Gleichgewicht: zu jedem Paar von Neigung und Geschwindigkeit gehört ein Kurvenradius. Der Fahrradfahrer kann in bestimmten Grenzen freihändig jede Kurve fahren. Weil der Neigungswinkel
NW = v2 k/g
vGeschwindigkeit
k Krümmung der Spur
gErdbeschleunigung
das Moment um die Lenkachse ausgleichen muss. – Die Kreiselmoment spielen insofern ein Rolle, als mit der Winkelgeschwindigkeit des Lenkeinschlags dLW/dt ein Moment um die Fahrzeuglängsachse entsteht, das dem Massenträgheitsmoment, der Winkelgeschwindigkeit des Rades und dLW/dt proportional ist. Der Fahrer kann mit Hilfe der Geschwindigkeit des Lenkeinschlagwinkels den Neigungswinkel beeinflussen. (Die Neigungsgeschwindigkeit bewirkt umgekehrt Kreiselmomente beider Räder um die Fahrzeughochachse.)
Auch die Lenkung eines Autos ist normalerweise instabil, Bild 3-2a. Die Vorderradlast baut in Folge des Nachlaufwinkels NW mit zunehmendem Lenkwinkel L ein destabilisierendes Moment um die Lenkachse auf (Mi = Vorderradlast · n · sin(NW) · sin(L)), das den Lenkwinkel zu vergrößern sucht. Diesem einschlagenden Lenkmoment steht ein Moment Mk aus der Krümmung der Fahrspur gegenüber, das den Lenkwinkel zu verringern sucht: ohne dieses Moment würden die Räder geradeaus rollen. (Die Aufstandsfläche muss entsprechend der Krümmung der Fahrspur gekrümmt werden. Die kurveninneren Schubkraftelemente treiben, die kurvenäußeren bremsen. Das führt zu einem Moment, das den Lenkwinkel zu verringern sucht.)
122 |
3 Lenken – Fahrzeugführung quer |
Die Spreizung führt zu einem rückdrehenden Moment um die Lenkachse, wenn der Lenkrollhalbmesser positiv ist:
Msp = Vorderradlast · NLR · sin (SPW) · (1 cos (L))
Weil es meist um kleine Lenkwinkel L geht und der Lenkrollhalbmesser klein oder 0 ist, wird dieser Einfluss nicht weiter beachtet. Für große Lenkwinkel L kann er aber durchaus eine Rolle spielen.
Auf die Lenkachse bezogen wirken für die Achse folgende Kräfte und Momente (Moment > 0 verkleinert den Lenkwinkel):
S = 46 800 ß (N) Seitenkraft durch Schräglauf, Ms = 936 ß (Nm)
Schräglaufmoment, Mi = -103 k,
Mk = 55 k, Mb = 651.
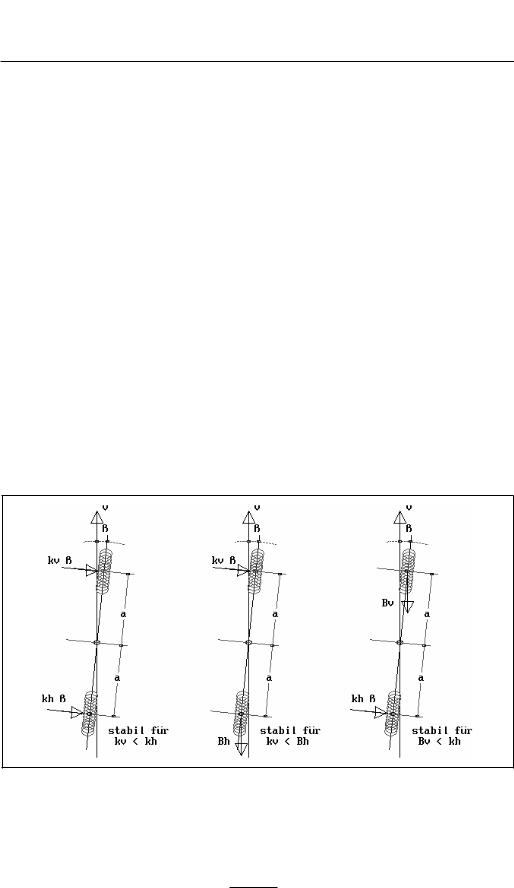
Bild 3-33 Links: Lenkmoment aus Nachlaufwinkel und Krümmung der Fahrspur Rechts: ist außerdem das Lenkmoment aus verschiedenen Seitenkräften
(Querbeschleunigung bq) berücksichtigt.
In Bild 3-33 sind links die Momente Mk und Mi dargestellt.
M1 = LVA ng SIN(NW) SIN(LW) |
einschlagendes Moment aus |
|
LVA |
Vorderachslast |
Nachlaufwinkel NW |
ng |
geometrischer Nachlauf |
|
LW |
Lenkwinkel |
|
M2 = 100 k rückdrehendes Moment aus Krümmung der Fahrspur (angenommen),
3.3 Stationäres Fahren |
123 |
M3 = Sv (ng + nr) Moment aus der Seitenkraft infolge Querbeschleunigung.
M1 hängt von der Achslast, dem geometrischen Nachlauf, dem Nachlaufwinkel und dem Lenkwinkel (für kleine Geschwindigkeiten Radstand · Krümmung k) ab,
M2 ebenfalls von der Achslast, vom Reibwert und vom Reifen ab (Schubweichheit der Stollen, Größe der Aufstandsfläche und damit Reifeninnendruck). (Auf Glatteis wird dieses Moment sehr klein: die Lenkung fühlt sich bei kleinen Geschwindigkeiten instabil an.)
M3 von der Masse der Vorderachse, der Querbeschleunigung v2 · k und vom geometrischen Nachlauf ng und dem Reifennachlauf nr.
Die vorstehenden Überlegungen können nur der prinzipiellen Klärung dienen. Tatsächlich treten andere Faktoren hinzu, von denen der wichtigste der Umstand ist, dass die Lauffläche gegen das Rad über den Torus des Reifenkörpers elastisch abgestützt ist >3.5 . Das bewirkt, dass der Seitenkraftbeiwert mit zunehmender Radlast ein Maximum erreicht und dann wieder abfällt (Bild 3-6, rechts).
3.3 Stationäres Fahren
Bewegt sich ein Fahrzeug translatorisch mit der Geschwindigkeit v und ist zufällig ein kleiner Winkel ß zwischen Fahrtrichtung und Fahrzeuglängsachse entstanden (Bild 3-34), dann treten an den Rädern die Seitenkräfte Sv und Sh auf (links). Soll der Störwinkel wieder kleiner werden, dann muss Sv · av < Sh · ah, oder bei av = ah · Εv < Εh sein.
Bild 3-34 Richtungsstabilität infolge der Seitenund Bremskräfte.
