
Mensch und Fahrzeug
.pdf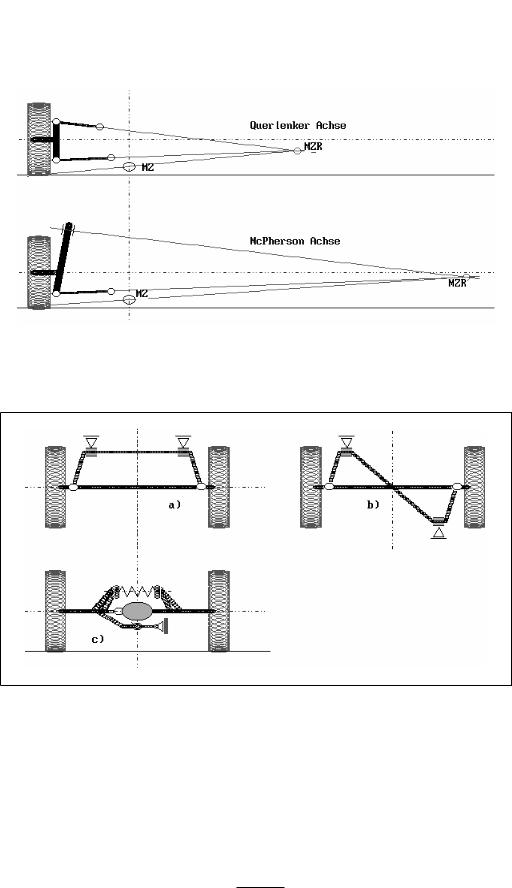
104 |
3 Lenken – Fahrzeugführung quer |
|
|
|
|
|
|
|
Bild 3-9 Lage des Momentanzentrums bei Einzelradaufhängung
Bild 3-10 Maßnahmen zur Veränderung der wechselseitigen Federung.
a)Drehstab-Stabilisator (nach einem Vorschlag H. Maruhn´s etwa 1930): bei gleichseitigem Einfedern der Achse bleibt der Drehstab wirkungslos; bei wechselseitigem Federn vergrößert er den Radlastunterschied.
b)Z-Stab (Porsche, 1960): bei wechselseitigem Einfedern bleibt der Drehstab wirkungslos; gleichseitiges Einfedern wird verhärtet.
c)Ausgleichfeder an einer Eingelenk-Pendelachse (Mercedes, 1959): Die Feder verhärtet das gleichsinnige Einfedern, spricht aber bei wechselseitigem Federn nicht an.

3.2 Reales Fahrzeug, Fahrdynamik |
105 |
Besondere Bedeutung hat die Erfindung des Drehstabes (Bild 3-10a) durch Herbert Maruhn >3.1 . Er erlaubt die wechselseitige Federung der betreffenden Achse zu verhärten und damit bei ihr eine Verringerung der Seitenführungskraft zugunsten der anderen Achse zu bewirken. Für die Fahrstabilität im Grenzbereich ist das die wichtigste Maßnahme. Mit härter werdendem Drehstab tritt eine Komfortverschlechterung ein, die man dadurch begrenzen kann, dass man die Radlaständerung an der anderen Achse verringert, durch einen Z-Drehstab oder eine Ausgleichsfeder, Bild 3-10b und c. (Porsche und Mercedes hatten diese Maßnahmen Ende der 50er Jahre.)
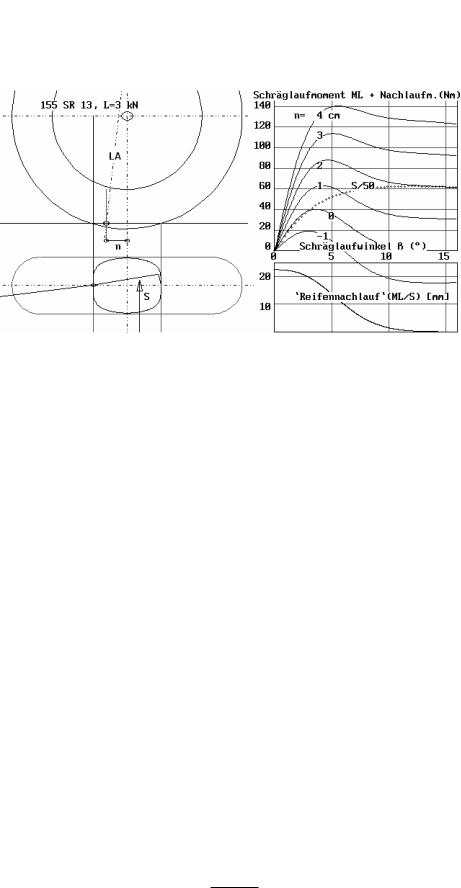
Bei kleinen Querbeschleunigungen ist die Lenkelastizität bestimmend für die Stabilität des Fahrzeuges >3.7 . In Bild 3-11 ist links ein nach links rollendes Rad in Aufund Grundriss dargestellt. Unter dem Einfluss einer Seitenkraft S läuft das Rad schräg. Die Seitenkraft greift hinter der Mitte der Aufstandsfläche an. Zusammen mit dem Nachlauf n ergibt sich ein Moment um die Lenkachse LA, das das Rad entsprechend der Elastizität in die Bewegungsrichtung hinein dreht, den Schräglaufwinkel und damit die Seitenkraft verkleinert. Bei festgehaltener Lenkung (fixed control) wirkt an der Vorderachse ein scheinbar kleinerer Schräglaufwinkel. Als Beispiel für ein neutrales Fahrverhalten bei Vorderrad-Antrieb kann der Mini gelten, der dies unter anderem mit seiner Hinterachskonstruktion erreicht, Beispiel 5.
Beispiel 5 Radführung: Agiles, zielgenaues und neutrales Fahrverhalten mit Zentrallenker-Hinterachse (Werkbild BMW/Mini)
106 |
3 Lenken – Fahrzeugführung quer |
|
|
|
|
|
|
|
Bild 3-11 Die Seitenkraft S greift hinter der Mitte der Berührungsfläche des Reifens mit der Fahrbahn an. Dieser „Reifennachlauf“ nimmt mit steigender Seitenkraft ab. Er beträgt zunächst etwa 1/6 der Länge der Berührungsfläche >3.5 . Der Reifennachlauf addiert sich zum Nachlauf aus der Geometrie der Radführung zum Nachlaufmoment, das dem Fahrer eine Information über die Größe der Seitenkraft liefert.
– Das Nachlaufmoment führt aber auch zu einer Deformation in der Lenkung zwischen Rad und Lenkrad. Bei festgehaltenem Lenkrad schlägt daher das Rad etwas ein und verringert so den effektiven Schräglaufwinkel.
Geht man davon aus, dass für die Fahrstabilität ein größerer Seitenkraftbeiwert hinten als vorn die notwendige und hinreichende Voraussetzung ist, dann stellt man fest, dass für kleine Querbeschleunigungen die Lenkelastizität, für große Querbeschleunigungen die Radlastdifferenz maßgebend ist.
Tatsächlich ist die Lenkelastizität nur eine (wichtige) unter anderen Elastizitäten in der Radführung, Bild 3-12. Dort ist angenommen, dass die Seitenkraft des Rades durch die Feder cQ und das Moment um die Lenkachse durch die Feder cL abgestützt wird. (Auch ein nicht gelenktes Rad hat eine „Lenkachse“: die gedachte Linie, die in der Mitte des Radaufstandspunktes die Fahrbahn durchstößt und um die das Rad lenkt.) Die „elasto-kinetische“ Führung aller Räder bestimmt bei gegebenen Reifenkennwerten die Größe der Seitenkräfte bei einer translatorischen Bewegung des Fahrzeuges.
|
3.2 Reales Fahrzeug, Fahrdynamik |
107 |
|
|
|
|
|
|
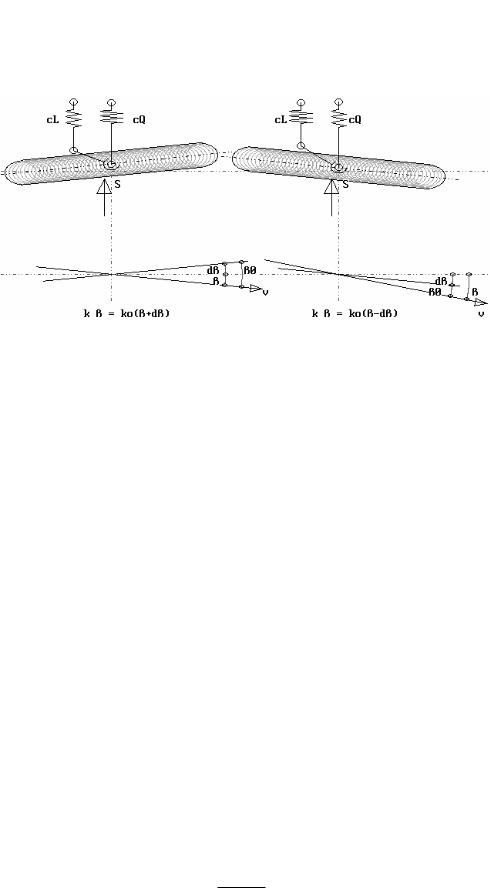
Bild 3-12 Durch Elastizitäten in der Radführung kann der effektive Seitenkraftbeiwert gesteuert werden. Die Elastizitäten stammen aus der Gummilagerung der Radführung, der elastischen Verformung aller Bauteile, insbesondere des Lenkhebels
Links ist angenommen, dass die Elastizität der Querabstützung cQ (N/m) kleiner als die der Abstützung des Nachlaufmoments cL ist. Aus dem Schräglaufen des Radpunktes mit dem Winkel ß folgt eine Seitenkraft und ein Nachlaufmoment, das das Rad um den Winkel dß lenkt. In diesem Fall vergrößert dß den Schräglaufwinkel ß. Der effektive Seitenkraftbeiwert k = ko (ß + dß) / ß (ko = Seitenkraftbeiwert des Rades).
Rechts ist angenommen, dass die Elastizität der Querabstützung cQ (N/m) größer als die der Abstützung des Nachlaufmoments cL ist. Aus dem Schräglaufen des Radpunktes mit dem Winkel ß folgt eine Seitenkraft und ein Nachlaufmoment, das das Rad um den Winkel dß lenkt. In diesem Fall verkleinert dß den Schräglaufwinkel ß. Der effektive Seitenkraftbeiwert k = ko (ß – dß)/ß.
Andere konstruktive Maßnahmen zur Beeinflussung der Fahrdynamik zeigen Bild 3-13 und 3-14.
108 |
3 Lenken – Fahrzeugführung quer |
|
|
|
|
|
|
|
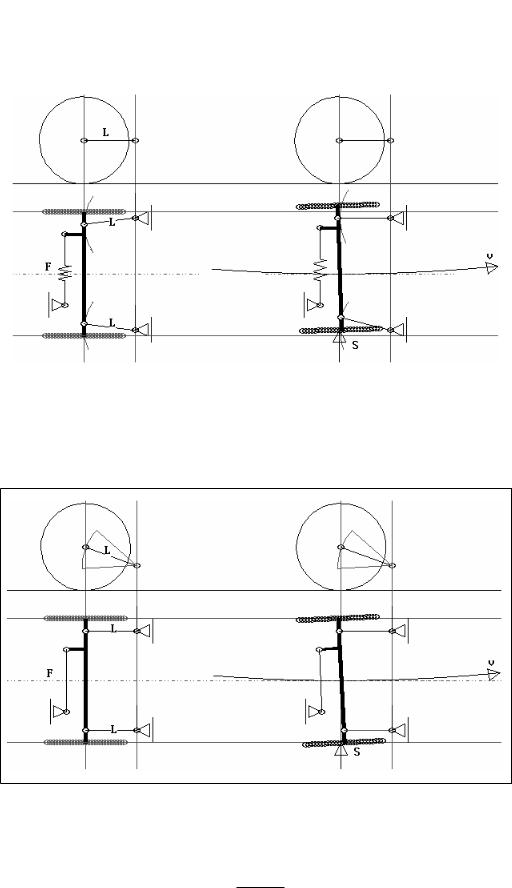
Bild 3-13 Seitenkraftlenken an einer starren Hinterachse, die von den Lenkern L geführt und durch einen elastischen Panhardstab F abgestützt ist. Beim Durchfahren einer Linkskurve (rechtes Bild) verschiebt die Querbeschleunigung (Seitenkraft S) die Achse zum Kurveninneren. Die Lenker L bewirken einen Lenkeinschlag, der das Fahrzeug aus der Kurve führt, stabilisiert.
Bild 3-14 Roll-Lenken an einer starren Hinterachse, die von den Lenkern L geführt wird. Beim wechselseitigen Einfedern lenkt die Achse aus der Kurve heraus.
|
3.2 Reales Fahrzeug, Fahrdynamik |
109 |
|
|
|
|
|
|
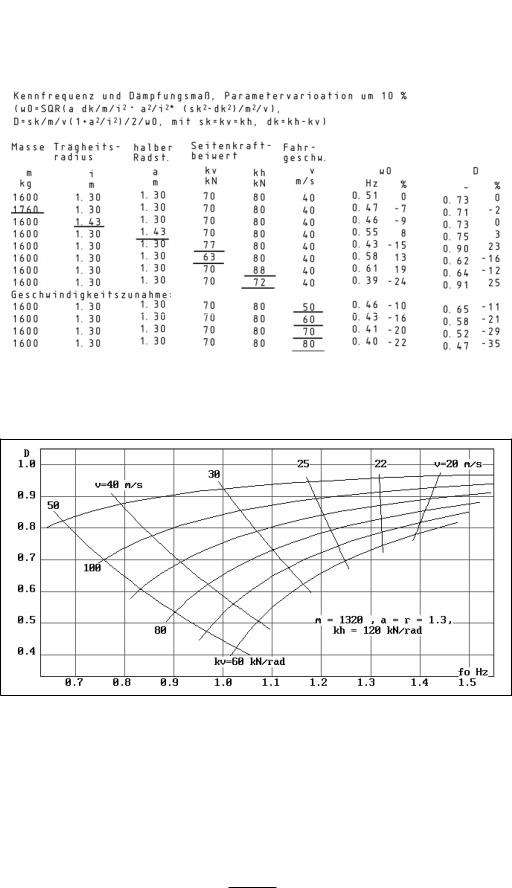
Bild 3-15 Kennfrequenz f0 und Dämpfungsmaß D: Variationen der Kenngrößen um +/– 10 %.
Bild 3-16 Dämpfungsmaß D als Funktion der Kennfrequenz f0 für verschiedene Seitenkraftbeiwerte vorn kv und Fahrgeschwindigkeiten v.
Einen Überblick über Kennfrequenz und Dämpfungsmaß eines PKWs gibt eine Parametervariation Bild 3-15 und Bild 3-16, die Lösung der Bewegungsgleichung und Lösungen bei stationärem Verhalten geben Bild 3-17 und 3-18.

110 |
3 Lenken – Fahrzeugführung quer |
|
|
|
|
|
|
|
Bild 3-17 Formeln zu 3-5: S = k · Ε (linearisiert).
A, B, C, D, psi, fi und Ε sind komplexe (vektorielle) Größen.
Bild 3-18 Formeln stationär mit Umfangskräften. (W … Fahrwiderstand, Uv und Un Umfangskraft am Rad)
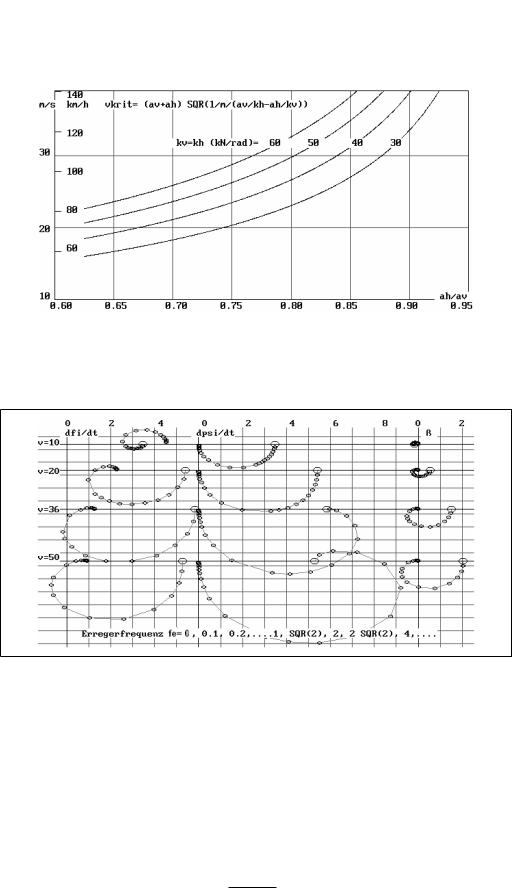
Wenn die Seitenkraftbeiwerte an Vorderund Hinterachse gleich groß sind, dann gibt es eine Geschwindigkeit vkrit, bei der jede Krümmung k mit dem Lenkeinschlag L = 0 gefahren werden kann. Bild 3-19 zeigt diese kritische Geschwindigkeit vkrit in Abhängigkeit von der Lage des Schwerpunktes, dem Verhältnis des Abstandes des Schwerpunktes von der Hinterachse ah und der Vorderachse av unter der Annahme, dass die Seitenkraftbeiwerte kv und kh gleich groß sind.
|
3.2 Reales Fahrzeug, Fahrdynamik |
111 |
|
|
|
|
|
|
Bild 3-19 Kritische Geschwindigkeit vkrit abhängig von der Schwerpunktlage
(Abstand Schwerpunkt-Vorderachse = av, Schwerpunkt-Hinterachse = ah) für gleiche Seitenkraftbeiwerte vorn und hinten (kv = kh).
Bild 3-20 Realteil und Imaginärteil von Schwimmwinkel Ε, Gierwinkelgeschwindigkeit dpsi/dt und Geschwindigkeit der Fahrtrichtungsänderung dfi/dt = k · v für v = 10 m/s und die angegebenen Fahrzeugwerte. Die Erregerfrequenz f verändert sich von Kreis zu Kreis in der angegebenen Sequenz.
Die Diskussion des Zeitverhaltens des Fahrzeuges kann mit Hilfe der Polbahnen, der Sprungantwort oder des Frequenzganges erfolgen. Bild 3-20 zeigt die Polbahnen von dfi/dt (Änderungs des Richtungswinkels f mit der Zeit), dpsi/dt (Änderung des Fahrzeugwinkels um die Hochachse psi mit der Zeit) und des Schwimmwinkels Ε für verschiedene Geschwindigkeiten. (Erreger ist der Einheitsvektor, der mit der Kreisfrequenz w = 2 pi · fe rotiert. Es ist jeweils der

112 |
3 Lenken – Fahrzeugführung quer |
Imaginärteil über dem Realteil aufgetragen, wobei die Frequenz von 0 bis 1 Hz in Stufen von 0.2 Hz, dann mit dem Faktor SQR(2) bis 3 Hz steigt.) Für die Erregerfrequenz fe = 0 (kleiner Kreis in der Polbahn) ist df/dt = dpsi/dt. Mit steigender Erregerfrequenz wird dann dpsi/dt = 0.
Der Schwimmwinkel Ε ist bei kleinen Fahrgeschwindigkeiten v negativ: das Hinterrad des Einspurmodells läuft innerhalb der Spur des Vorderrads. Bei der Fahrgeschwindigkeit v = 11.6 m/s und fe = 0 ist Ε = 0. Für größere Fahrgeschwindigkeiten ist Ε > 0.
Die Bilder 3-21 bis 3-23 untersuchen die realistische Sprungantwort. Der Lenkwinkel L „springt“ in etwa 0.2 s von 0 auf 0.87°. Richtungswinkel f, Gierwinkel psi und Schwimmwinkel Ε folgen je nach Fahrgeschwindigkeit gedämpft mit zunehmendem Überschwingen. Der Schwimmwinkel Ε wird zunächst negativ, weil die Vorderachse die Seitenkraft schneller aufbaut als die Hinterachse.
Bild 3-21 Sprungantwort der Richtungswinkelgeschwindigkeit dfi/dt, Gierwinkelgeschwindigkeit dpsi/dt und des Schwimmwinkels Ε für die Geschwindigkeiten v = 20, 30, 40 und 50 m/s.
Die Lenkwinkelverstellung L wird innerhalb von etwa 0.2 s aufgebracht (rechtes Bild). Das Überschwingen nimmt mit der Fahrgeschwindigkeit zu.
Bild 3-22 zeigt den Einfluss des Seitenkraftbeiwertes vorn kv bei den Fahrgeschwindigkeiten v = 20 und 40 m/s. Bei kleinerem kv steigen die Werte rascher an, sind aber schlechter gedämpft.
|
3.2 Reales Fahrzeug, Fahrdynamik |
113 |
|
|
|
|
|
|
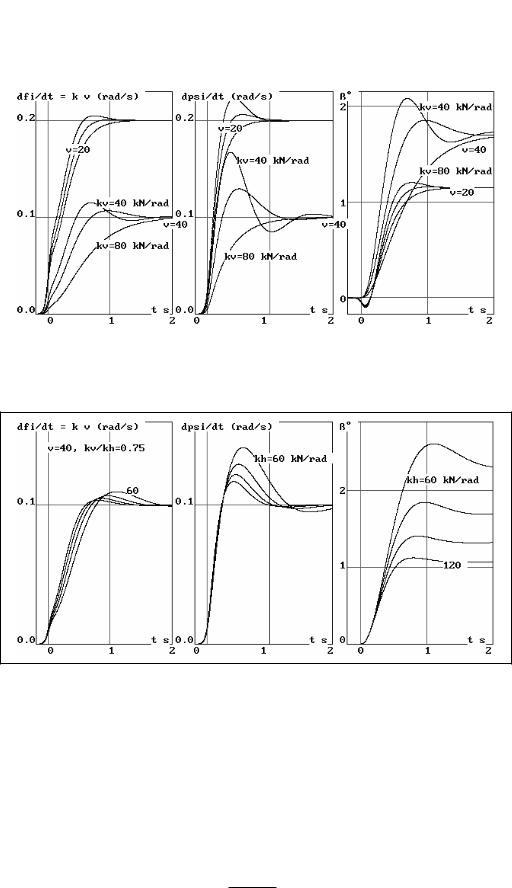
Bild 3-22 Wie 3-21, aber zusätzlich ist der Seitenkraftbeiwert vorn kv variiert (kv = 40, 60 und 80 kN/rad).
Bild 3-23 Wie 3-22, aber Variation des Seitenkraftbeiwerts hinten (kh = 60, 80, 100 und 120 kN/rad).
Den Einfluss der Lenkradverstellung untersuchen die Bilder 3-24 und 3-25. Die Lenkung wird in Form einer Glockenkurve verstellt, links langsam, rechts hastig. Wird der Lenkwinkel innerhalb einer Sekunde aufgebaut und innerhalb der nächsten wieder zurückgenommen, dann folgt die Krümmung der Fahrspur des Fahrzeugs mit einer Verzögerung von etwa 0.25 s. Bei der hastigen Lenkradverstellung rechts zerfällt die Antwort in zwei Teile: einen direkten Teil und ein Nachschwingen mit der Kennfrequenz des Fahrzeuges. Dieses Nachschwingen wird von den Fahrern negativ beurteilt.
