
- •Раздел 2. Кинетика простой необратимой реакции
- •Раздел 3. Кинетика реакции n-го порядка
- •Лекция 3. Кинетика обратимой реакции
- •Раздел 1. Кинетическая модель обратимой реакции в общем виде
- •Раздел 2. Кинетика обратимой реакции а r
- •Лекция 4. Кинетика параллельной реакции
- •Раздел 1. Кинетическая модель параллельной реакции в общем виде
- •Раздел 2. Кинетика параллельной реакции а s
- •Раздел 3. Селективность параллельной реакции а
Лекция 4. Кинетика параллельной реакции
Сложная реакция (параллельная, последовательная, смешанная) представляет собой взаимосвязанные простые реакции. Скорость изменения количества j–го вещества Wj , участвующего в m простых реакциях, равна алгебраической сумме скоростей этих реакций, умноженных на стехиометрический коэффициент j–го вещества в этих реакциях:

где νji – стехиометрический коэффициент j–го компонента в i–й реакции («+» для продукта реакции, «–» для исходного вещества); ri – скорость i–й реакции, записанная на основе ЗДМ.
Раздел 1. Кинетическая модель параллельной реакции в общем виде
Рассмотрим параллельную реакцию типа:
νА1А1 → νRR (4.1)
νА2А2 → νSS (4.2)
Кинетическая модель указанной реакции имеет вид:
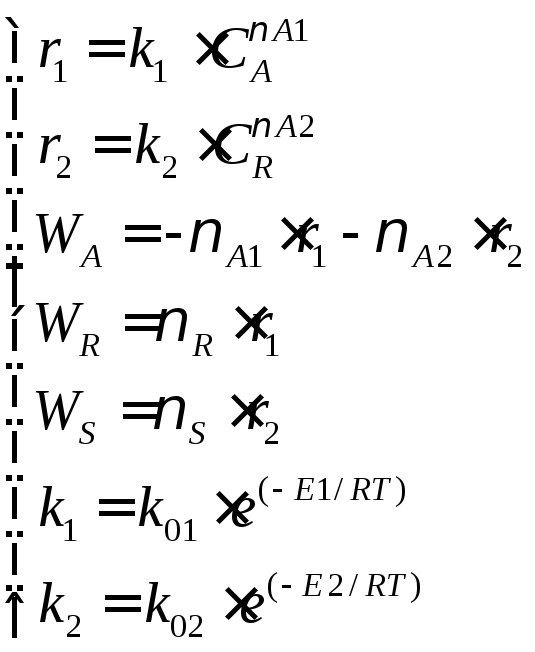 (4.3)
(4.3)
где r1 r2 – скорости образования веществ R и S, записанные на основе ЗДМ. При этом константы скорости реакций (4.1) и (4.2) не равны между собой: к1 ≠ к2.
Найдем решение этой системы для гомогенной параллельной реакции, протекающей по схеме:
 R
R
 А
А
S
 R
R
Раздел 2. Кинетика параллельной реакции а s
Зададимся начальными условиями:
T,V = const;
С А
= САо
при τ
= 0
А
= САо
при τ
= 0
СR = СRо =0
СS = СSо =0
Если V = const, то скорость реакции:
![]() (4.4)
(4.4)
![]() (4.5)
(4.5)
![]() (4.6)
(4.6)
Составим кинетическую модель рассматриваемой реакции при условии, что к1 ≠ к2:

Сопоставим выражения (4.4) и (4.7), (4.5) и (4.8), (4.6) и (4.9):

Определим изменение концентрации реагента А в ходе реакции.
Рассмотрим выражение (4.10). Разделим переменные, интегрируем от САо до СА и от 0 до τ :


![]() (4.13)
(4.13)
Выражение (4.13) представляет искомую зависимость СА = f(τ).
Изменение концентрации вещества R мы найдем, подставив выражение (4.13) в выражение (4.11):
![]()
Разделим переменные, интегрируем по концентрации от 0 до СR и от 0 до τ по времени:



 (4.14)
(4.14)
Выражение (4.14) представляет искомую зависимость СR = f(τ).
Концентрация вещества S может быть найдена аналогично, если подставить выражение (4.13) в выражение (4.12). После преобразований получим:
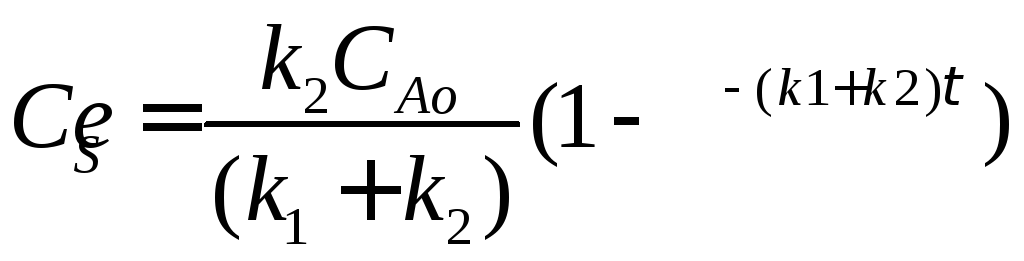 (4.15)
(4.15)
Выражение (4.15) представляет искомую зависимость СS = f(τ).
 R
R
Раздел 3. Селективность параллельной реакции а
S
Для сложных реакций, в которых кроме основной реакции протекают и побочные и, следовательно, кроме основных продуктов образуются и побочные продукты, для таких реакций важнейшим показателем их проведения является селективность.
Пусть R – целевой продукт, а S – побочный; и константа скорости реакции с участием вещества R больше, чем для реакции с веществом S (к1 > к2). Тогда общая или интегральная селективность продукта R для рассматриваемой параллельной реакции в соответствии с определением селективности будет равна:

Подставим в это выражение значения СА, и СR из (4.13) и (4.14) и так как
νА = νR = νS = 1, получим:

Мгновенная или дифференциальная селективность продукта R в соответствии с определением:
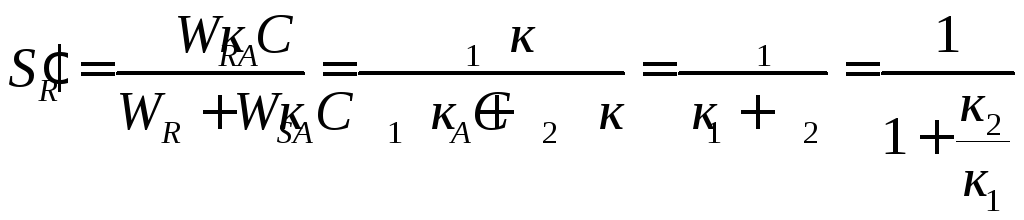
Вывод: для рассматриваемой параллельной реакции интегральная и дифференциальная селективность равны и в ходе реакции не изменяются:

Изобразим графически зависимости СА, СR,CS = f(τ), а также изменение селективности для параллельной реакции.

Из представленного следует, что для рассматриваемой параллельной реакции концентрация реагента А уменьшается в ходе реакции по экспоненциальной зависимости. Эта зависимость аналогична изменению концентрации реагента А для простой необратимой реакции. Концентрации продуктов R и S экспоненциально возрастают, но в разной степени. Концентрация продукта R растет быстрее и достигает большего значения, чем концентрация вещества S, поскольку к1 > к2. Что касается селективности, то, как было уже отмечено выше, для рассматриваемой параллельной реакции интегральная и дифференциальная селективность равны и в ходе реакции не изменяются.
