5. Численное дифференцирование

Задача 5.Вычислить производную от указанной в приложении 2 функции в точке с помощью конечноразностной формулы второго порядка точности на двух сетках. Воспользовавшись формулами Рунге – Ромберга, 1) оценить погрешность результатов; 2) вычислить значение производной с более высоким порядком точности.

Указания к решению

• выбрав значение шага hсетки, вычисляют узловые значения аргумента (изображая их на числовой оси) и дифференцируемой функции;

• подставив эти данные в ко

• нечноразностную формулу, вычисляют значение производной ;

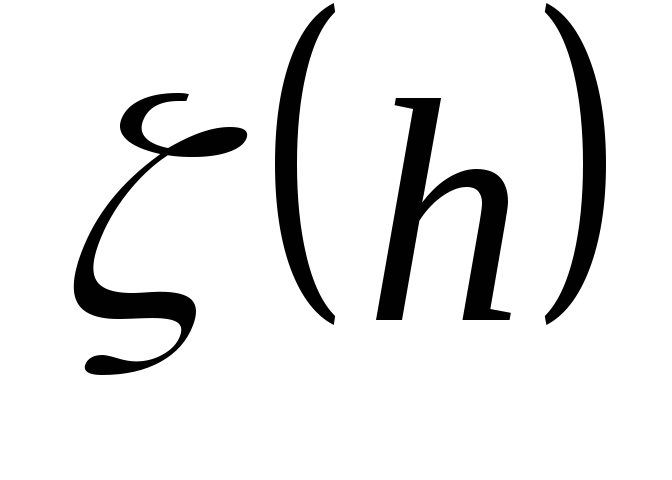• выбрав другое значение шага rhсетки, вычисляют узловые значения аргумента (изображая их на прежнем рисунке) и дифференцируемой функции;

• подставив эти данные в конечноразностную формулу, вычисляют значение производной ;

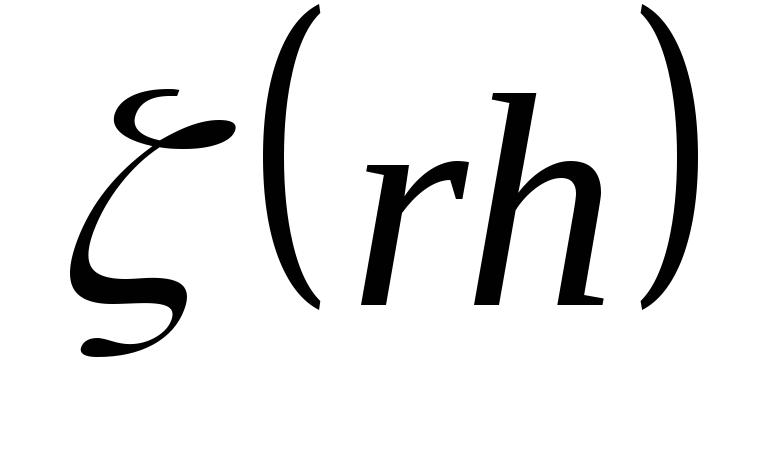• используя полученные значения во второй формуле Рунге – Ромберга, вычисляют погрешность значения производной;

• используя полученные значения в первой формуле Рунге – Ромберга, вычисляют значение производной с повышенным порядком точности (необходимо указать каким порядком);

• вычисляется точное значение производной от заданной функции и по этому результату сопоставляются полученные оценки погрешности, делаются выводы.

6. Вычисление интегралов

Задача 6.Вычислить определенный интеграл от указанной в приложении 3 функции с помощью обобщенной формулы трапеций на сетке с тремя узлами, предварительно априорно оценив погрешность. Вычислив этот же интеграл на сетке с вдвое меньшим шагом, с помощью формул Рунге - Ромберга 1) определить погрешность решения и 2) получить значение интеграла с повышенным порядком точности.

Указания к решению

• вычислив значение шага hсетки и значения производной от подынтегральной функции на краях интервала интегрирования, априорно оценивают погрешность квадратурной формулы на данной сетке;

• вычисляют узловые значения аргумента (изображая их на числовой оси) и подынтегральной функции;

• подставив вычисленные значения в квадратурную формулу, вычисляют приближенное значение интеграла I(h);

• взяв вдвое меньшее значение шага h/2 сетки, вычисляют узловые значения аргумента (изображая их на числовой оси) и подынтегральной функции;

• подставив вычисленные значения в квадратурную формулу, вычисляют приближенное значение интеграла I(h/2);

• используя полученные значения во второй формуле Рунге – Ромберга, вычисляют погрешность значения интеграла;

• используя полученные значения в первой формуле Рунге – Ромберга, вычисляют значение производной с повышенным порядком точности (необходимо указать каким порядком).

7. Решение систем линейных алгебраических уравнений (слау)

Задача 7. Решить систему трех линейныхалгебраических уравнений методом Гаусса и сделать проверку. Коэффициенты при неизвестных и свободные члены этих уравнений приведены в приложении 4.

Указания к решению.

А.Записывают систему в виде расширенной матрицы и проводят с ней все действия.

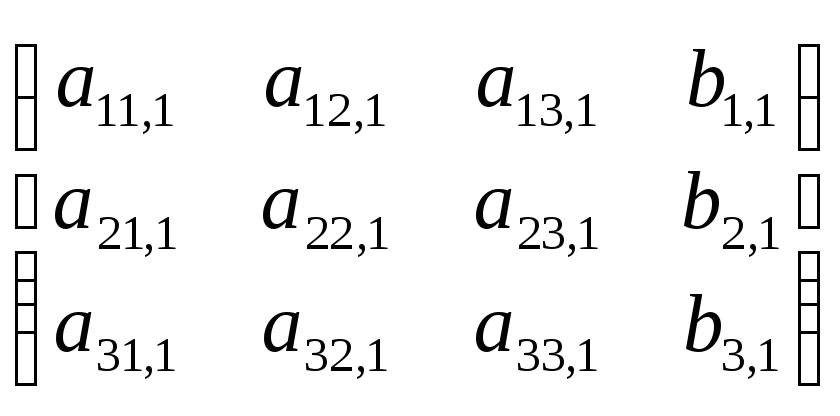(1)

Б. Записывают систему с учетом выбора главного элемента.

(2)

В. Разделив первое уравнение на главный элемент , получают:

(3)

Исключают из второго уравнения системы (2) первое слагаемое, вычитая из него уравнение (3), умноженное на .Также исключают первое слагаемое в остальных уравнениях.

Система уравнений с учетом уравнения (3) принимает следующий вид:

(4)

Г. Записывают систему (4) с учетом выбора главного элемента.

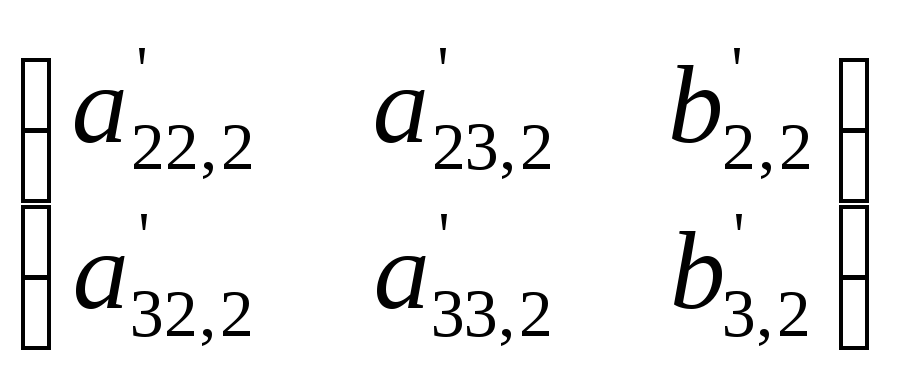(5)

Разделив первое уравнение системы (5) на главный элемент , получают:

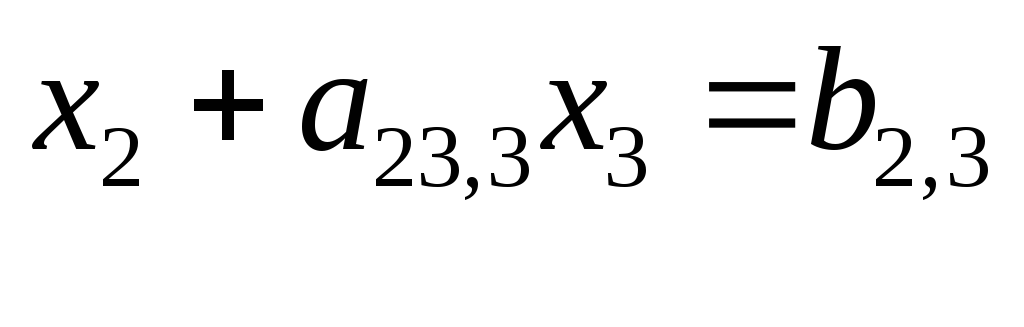(6)

Исключают из второго уравнения системы (5) первое слагаемое, вычитая из него уравнение (6), умноженное на .

Система уравнений с учетом уравнений (3),(6) принимает вид:

(7)

Решая уравнение (7), получают :

(8)

Д. Решение системы (1) получают последовательно решая уравнения (8),(6),(3).

Е. Проверяют полученное решение, подставляя его в систему (1).

Ж. Опредилитель системы (1) вычисляют по формуле:

, где- число перестановок уравнений в результате выбора главных элементов.

Задача 8. Решить систему трех линейных алгебраических уравнений методом квадратного корня. Коэффициенты при неизвестных и свободные члены этих уравнений приведены в приложении 4.

Указания к решению.

А. Для нахождения элементов матриц SиDзаписывают разложение исходной матрицыA=S^ТDSв покомпонентном виде.

Б. Записывают матрицу S иD.

B. Представляя исходную СЛАУ эквивалентной трем СЛАУ,,решают их относительно,и.

Г. Проверяют полученное решение, сопоставляя его с решением СЛАУ методом Гаусса.

Д. Опредилитель данной системы вычисляют по формуле:

,

где р– количество отрицательных элементов матрицыD.