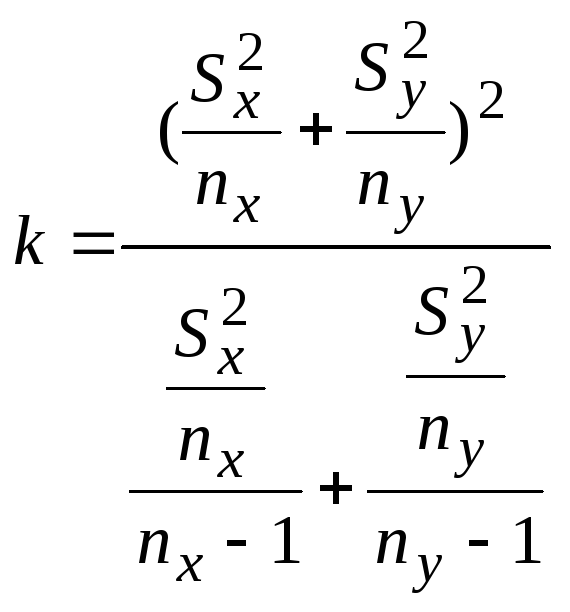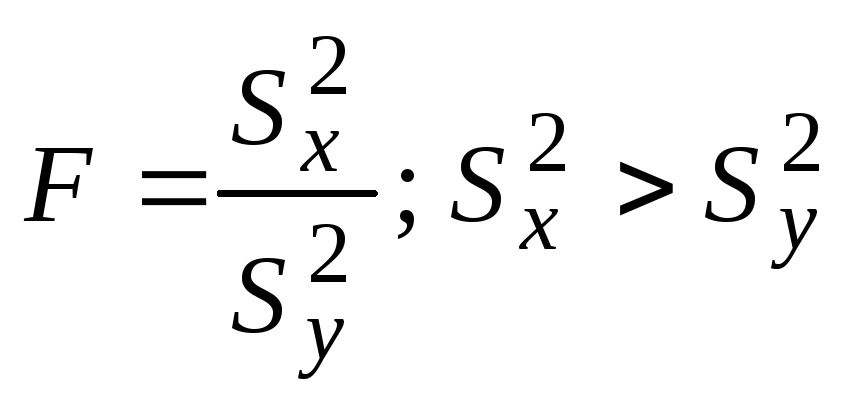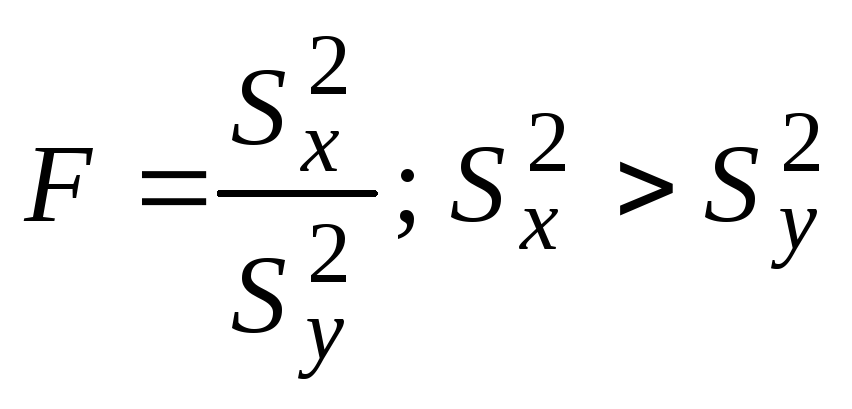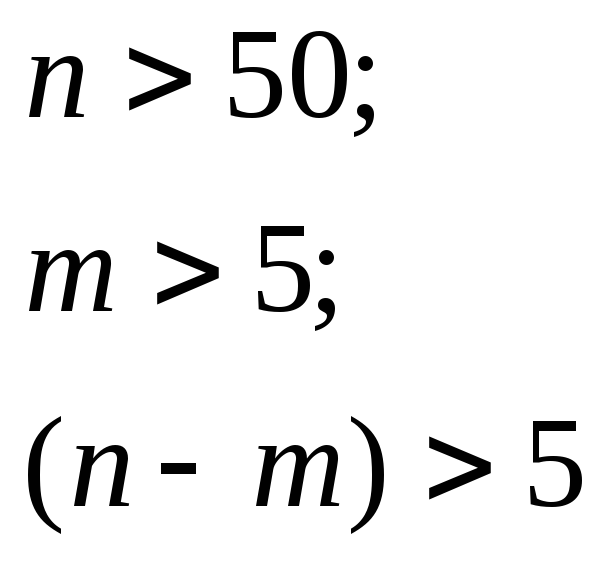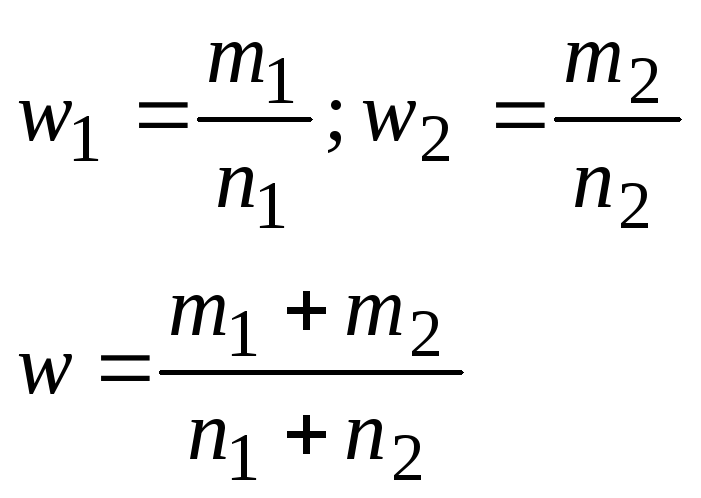5.8 Использование критерия согласия Пирсона

Критерий согласия -Пирсона позволяет осуществлять проверку эмпирического и теоретического (либо другого эмпирического) распределений одного признака. Данный критерий применяется, в основном, в двух случаях:

• для сопоставления эмпирического распределения признака с теоретическим распределением (нормальным, показательным, равномерным либо каким-то иным законом);

• для сопоставления двух эмпирических распределений одного и того же признака.

Идея метода – определение степени расхождения соответствующих частот и ; чем больше это расхождение, тем больше значение :

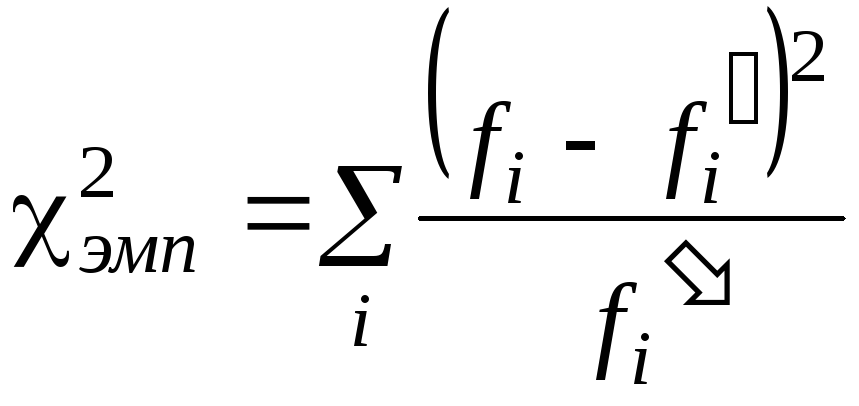
Объемы выборок должны быть не меньше 50 и необходимо равенство сумм частот .

Нулевая гипотеза H₀={два распределения практически не различаются между собой}; альтернативная гипотеза – H1={расхождение между распределениями существенно}.

Приведем схему применения -критерия для сопоставления двух эмпирических распределений:

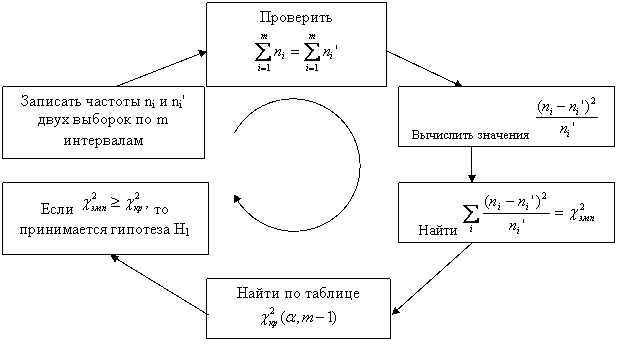
Пример использования критерия Пирсона

Среди школьников с 1 по 7 класс в течение двух недель проводился опрос об удовлетворенности собственными оценками. Результаты опроса представлены в таблице:

Таблица

Класс	Число удовлетворенных оценками в первую неделю исследования	Число удовлетворенных оценками на второй неделе исследования
1	16	17
2	13	13
3	8	9
4	11	9
5	4	3
6	3	4
7	3	3

Можно ли считать, что эмпирическое распределение на первой неделе исследования согласуется с эмпирическим распределением на второй неделе исследования, т.е. структура удовлетворенности ответами учащихся сохранилась в течение данного времени?

Вычислим эмпирическое значение критерия:

По таблице критических точек распределения по принятому уровню значимости 0,05 и числу степеней свободы k=7-1 находим критическую точку .

Поскольку , то нет оснований отвергать нулевую гипотезу об одинаковом распределении мнений учащихся о своей успеваемости в разные недели.

5.9 Проверка статистических гипотез применительно к таблицам сопряженности

Таблица сопряженности - средство представления совместного распределения двух переменных, предназначенное для исследования связи между ними. Таблица сопряженности является наиболее универсальным средством изучения статистических связей, так как в ней могут быть представлены переменные с любым уровнем измерения.

Строки таблицы сопряженности соответствуют значениям одной переменной, столбцы - значениям другой переменной (количественные шкалы предварительно должны быть сгруппированы в интервалы). На пересечении строки и столбца указывается частота совместного появления соответствующих значений двух признаков и. Сумма частот по строкеназывается маргинальной частотой строки; сумма частот по столбцу- маргинальной частотой столбца. Сумма маргинальных частот равна объему выборки; их распределение представляет собой одномерное распределение переменной, образующей строки или столбцы таблицы.

В таблицах сопряженности могут быть представлены как абсолютные, так и относительные частоты (в долях или процентах). Относительные частоты могут рассчитываться по отношению:

• к маргинальной частоте по строке

• к маргинальной частоте по столбцу

• к объему выборки

Таблицы сопряженности используются для проверки гипотезы о наличии связи между двумя признаками, а также для измерения тесноты связи.

Для анализа таблиц сопряженности при проверке гипотезы о наличии связи между двумя признаками может быть использован критерий "хи-квадрат".

Гипотеза H0: переменные инезависимы.

Пусть имеется таблица сопряженности , построенная для переменныхи:

	1	...		...
1
...
...

Введем следующие обозначения:

- наблюдаемая частота для соответствующей ячейки;

- ожидаемая частота в случае правильности нулевой гипотезы.

Тогда статистика "хи-квадрат" может быть рассчитана по формуле:

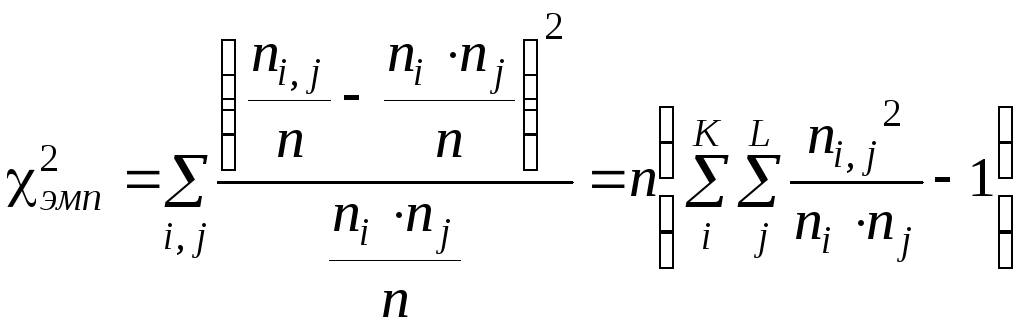
Условия применимости:

• ;

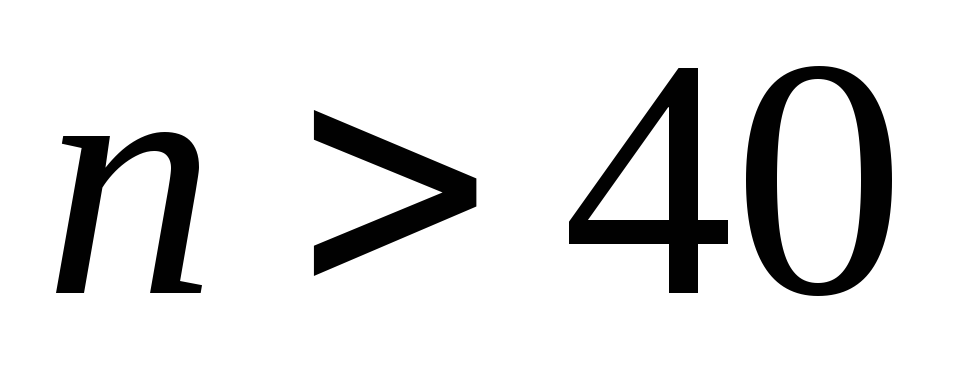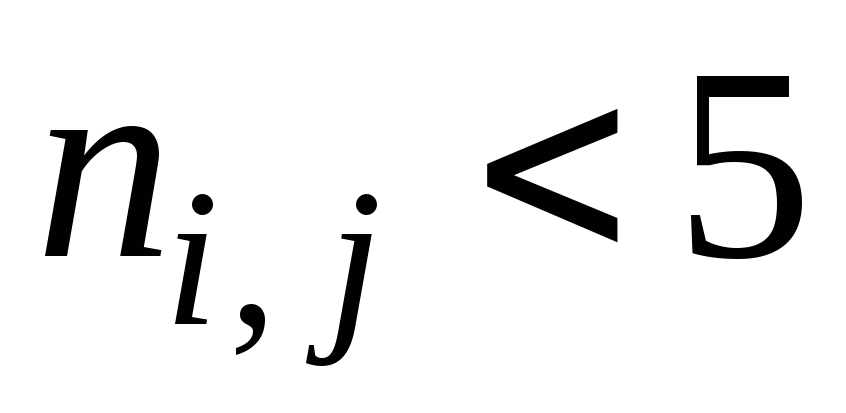• не более чем в 20% ячеек n>40.

Эмпирическое значение критерия сравнивается с критическим . Если эмпирическое значение критерия не больше критического, то нулевая гипотеза не отвергается и переменныеина выбранном уровне значимости могут считаться независимыми.

Для частного случая таблица сопряженности принимает вид:

1	2
1	a	b
2	c	d

Статистика рассчитывается по упрощенной формуле:

Пример применения критерия

Эффективны ли занятия на подготовительных курсах (ПК) при поступлении на факультет информатики и управления (ИФ). Данные о поступивших на факультет ИФ ХПИ представлены в таблице:

	Поступили	Не поступили
Ходили на ПК
Не ходили на ПК

Нулевая гипотеза H0: ПК не эффективны.

В данном случае , следовательно, можно применить упрощенную формулу:

Критическое значение критерия , следовательно

,

Гипотеза H0 отвергается, т.е. ПК эффективны для поступления на НТУ «ХПИ».

Критерий Мак-Немара

Критерий Мак-Нимара (также, К. Мак-Немара, англ. McNemar's test) используется для анализа таблиц сопряженности размером 2x2 (для дихотомического признака). В отличие от критерия хи-квадрат, критерий Мак-Немара применяется, когда условие независимости наблюдений не просто не выполняется, но, напротив, учет признака выполняется на одних и тех же субъектах.

Этот тест проводится в следующих случаях:

• для одной и той же выборки определяются значения двух дихотомических переменных (например, любовь к сладкому и предпочтение чая или кофе);

• для одной и той же выборки определяется значение одной дихотомической переменной до воздействия и после воздействия (например, отношение к товару до и после просмотра рекламы).

Пусть дихотомическая переменная принимает значенияи, а дихотомическая переменнаяпринимает значенияи.

	Переменная		Сумма в строке
Переменная
	a	b	a + b
	c	d	c + d
Сумма в столбце	a + c	b + d	n

Нулевая гипотеза утверждает, что маргинальные распределения для всех исходов совпадают:

Расчет эмпирического значениякритерия производится (дляb≠c) следующим образом:

а) если b+c=q≤20, то находится по таблице M(n,m), где m=min(b,c).

б) если b+c>20, то вычисляется по формуле

Приb=cрекомендуется использовать -критерий.

Определение критического значения зависит от способа определения эмпирического значения.

Алгоритм применения критерия Макнамары можно описать следующей схемой:

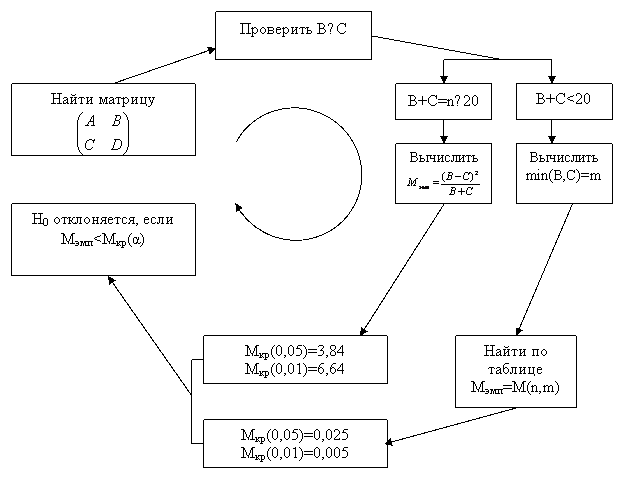
Для повышения качества критерия на выборках с низкочастотными событиями применяют скорректированную формулу Йейтса:

или скорректированную формулу Эдвардса:

Пример применения критерия Мак-Немара

Учащиеся тестировались до и после проведения тренинга по повышению качества усвоения учебного материала Экспериментальные данные, представляют итог прохождения теста: «+» – тест пройден успешно; «–« – тест не пройден.

Результаты представлены в четырехпольной таблице.

		Второе тестирование
		Справились	Не справились
Первое тестирование	Справились	A=50	B=19
	Не справились	C=31	D=20

Можно ли сказать, что успешность учащихся изменилась существенно?

Нулевая гипотеза H0={различие значений исследуемого показателя до и после эксперимента несущественно};

Альтернативная гипотеза –H1={различие показателя до и после эксперимента существенно}.

В приведенном примере в≠с, поэтому применение критерия Макнамары допустимо. Сумма в+с=19+31=50>20, поэтому:

На уровне значимости 5%. Следовательно, нулевая гипотеза на данном уровне значимости отклоняется, и различия в уровне успеваемости существенны.

Таблица Классификация и назначение тестов

	Две независимые выборки	Две зависимые выборки	Сравнение параметра с эталоном	Несколько независимых выборок	Несколько зависимых выборок
Параметрические тесты	t-критерий Стьюдента	t-критерия Стьюдента	t-критерия Стьюдента
	Критерий Крамера-Уэлча
Непараметрические тесты	Критерий Манна — Уитни	T-критерий Вилкоксона		Критерий Крускала-Уоллиса	Критерий Фридмана
		Тест знаков
		Критерий Макнамары (для биномиальных данных)

Приложение 1

Таблица 1. Проверка статистических гипотез

Исходные данные	Проверяемые гипотезы	Допущение	Точечные оценки параметров	Статистика	Критерий (двусторонний)
Проверка гипотезы о значении среднего нормально распределенной генеральной совокупности
- выборка объемомиз генеральной совокупности		Дисперсия генеральной совокупности известна и равна	где	, где
-«-		Дисперсия генеральной совокупности неизвестна	, где;	, где
Проверка гипотезы о равенстве средних двух нормально распределенных генеральных совокупностей
; - выборки объемом соответственноииз двух генер. совокупностей.		Дисперсии генеральных совокупностей известны и равны и	где;	, где
-«-		Дисперсии генеральных совокупностей неизвестны. Гипотеза о равенстве дисперсий верна.	,где,	, где	Двусторонний
-«-		Дисперсии генеральных совокупностей неизвестны. Гипотеза о равенстве дисперсий неверна.	-«-	, где	Двусторонний , где
Проверка гипотезы о равенстве дисперсий двух нормально распределенных генеральных совокупностей
;- выборки из двух генеральных совокупностей объемом соответственнои.		Математические ожидания известны и равны соответственно и
-«-		Математические ожидания неизвестны
Проверка гипотезы о значении параметра биномиально распределенной совокупности ( доли)
- количество экспериментов;- количество успехов в эксперименте				, где
Проверка гипотезы о равенстве долей успешных исходов экспериментов в двух совокупностях
- количество экспериментов;- количество успехов в экспериментах				, где

Приложение 2 Критические значения критерия U Манна-Уитни

(для проверки ненаправленных альтернатив) Р=0,05

N2	N1
	7	8	9	10	11	12	13	14	15	16	17	18	19	20
3	I	2	2	3	3	4	4	5	5	6	6	7	7	8
4	3	4	4	5	6	7	8	9	10	11	11	12	13	13
5	5	6	7	8	9	11	12	13	14	15	17	18	19	20
6	6	8	10	11	13	14	16	17	19	21	22	24	25	27
7	8	10	12	14	16	18	20	22	24	26	28	30	32	34
8	10	13	15	17	19	22	24	26	29	31	34	36	38	41
9	12	15	17	20	23	26	28	31	34	37	39	42	45	48
10	14	17	20	23	26	29	33	36	39	42	45	48	52	55
11	16	19	23	26	30	33	37	40	44	47	51	55	58	62
12	18	22	26	29	33	37	41	45	49	53	57	61	65	69
13	20	24	28	33	37	41	45	50	54	59	63	67	72	76
14	22	26	31	36	40	45	50	55	59	64	67	74	78	83
15	24	29	34	39	44	49	54	59	64	70	75	80	85	90
16	26	31	37	42	47	53	59	64	70	75	81	86	92	98
17	28	34	39	45	51	57	63	67	75	81	87	93	99	105
18	30	36	42	48	55	61	67	74	80	86	93	99	106	112
19	32	38	45	52	58	65	72	78	85	92	99	106	113	119
20	34	41	48	55	62	69	76	83	90	98	105	112	119	127

Р=0,01

N2	N1
	7	8	9	10	11	12	13	14	15	16	17	18	19	20
3			0	0	0	1	1	1	2	2	2	2	3	3
4	0	1	1	2	2	3	3	4	5	5	6	6	7	8
5	1	2	3	4	4	6	7	7	8	9	10	11	12	13
6	3	4	5	6	6	9	10	11	12	13	15	16	17	18
7	4	6	7	9	9	12	13	15	16	18	19	21	22	24
8	6	7	9	11	11	15	17	18	20	22	24	26	28	30
9	7	9	11	13	13	18	20	22	24	27	29	31	33	36
10	9	11	13	16	16	21	24	26	29	31	34	37	39	42
11	10	13	16	18	18	24	27	30	33	36	39	42	45	48
12	12	15	18	21	21	27	31	34	37	41	44	47	51	54
13	13	17	20	24	24	31	34	38	42	45	49	53	56 .	60
14	15	18	22	26	26	34	38	42	46	50	54	58	63	67
15	16	20	24	29	29	37	42	46	51	55	60	64	69	73
16	18	22	27	31	31	41	45	50	55	60	65	70	74	79
17	19	24	29	34	34	44	49	54	60	65	70	75	81	86
18	21	26	31	37	37	47	53	58	64	70	75	81	87	92
19	22	28	33	39	39	51	56	63	69	74	81	87	93	99

Приложение 3 Граничные значения числа серий (критерий серий Вальда—Вольфовица)

	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
6	3	3	3	-	-	-	-	-	-	-	-	-	-	-	-	-	-
7	3	3	4	4	-	-	-	-	-	-	-	-	-	-	-	-	-
8	3	3	4	4	5	-	-	-	-	-	-	-	-	-	-	-	-
9	3	4	4	5	5	6	-	-	-	-	-	-	-	-	-	-	-
10	3	4	5	5	6	6	6	-	-	-	-	-	-	-	-	-	-
11	3	4	5	5	6	6	7	7	-	-	-	-	-	-	-	-	-
12	4	4	5	6	6	7	7	8	8	-	-	-	-	-	-	-	-
13	4	4	5	6	6	7	8	8	9	9	-	-	-	-	-	-	-
14	4	5	5	6	7	7	8	8	9	9	10	-	-	-	-	-	-
15	4	5	6	6	7	8	8	9	9	10	10	11	-	-	-	-	-
16	4	5	6	6	7	8	8	9	10	10	11	11	11	-	-	-	-
17	4	5	6	7	7	8	9	9	10	10	11	11	12	12	-	-	-
18	4	5	6	7	8	8	9	10	10	11	11	12	12	13	13	-	-
19	4	5	6	7	8	8	9	10	10	11	12	12	13	13	14	14	-
20	4	5	6	7	8	9	9	10	11	11	12	12	13	13	14	14	15

Приложение 4 Критические значения статистики Колмогорова-Смирнова