5.5.3 Сравнение двух независимых выборок. Тест Колмогорова-Смирнова

Данный критерий позволяет оценить существенность различий между двумя выборками. Его применение возможно также для сравнения эмпирического распределения с теоретическим.

Объёмы рассматриваемых выборок должны быть достаточно большими: ≥50,≥50. Для использования теста выборки должны быть представлены в виде частотного распределения, при этомчисло категорий должно быть небольшим (до 7-9).

Нулевая гипотеза H0={различия между двумя распределениями недостоверны}.

Критерий позволяет найти категорию, в которой сумма частот расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.

Алгоритм проверки:

1. Определяются категории значений признака.

2. Строится частотное распределение каждой выборки по выделенным категориям.

3. Вычисляются относительные частоты 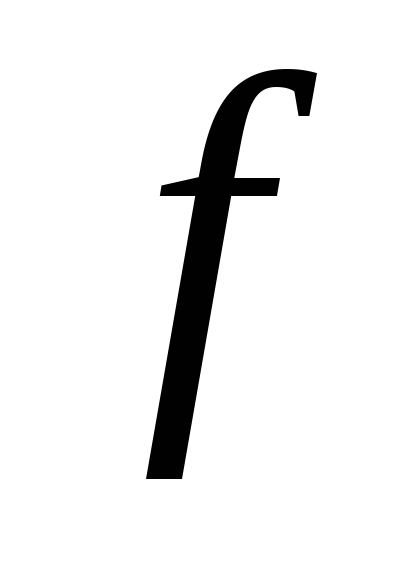, равные частному от деления частот на объём выборки, для каждой из имеющихся выборок.

4. Определяется модуль разности соответствующих относительных частот.

5. Определяется наибольший модуль, который обозначается .

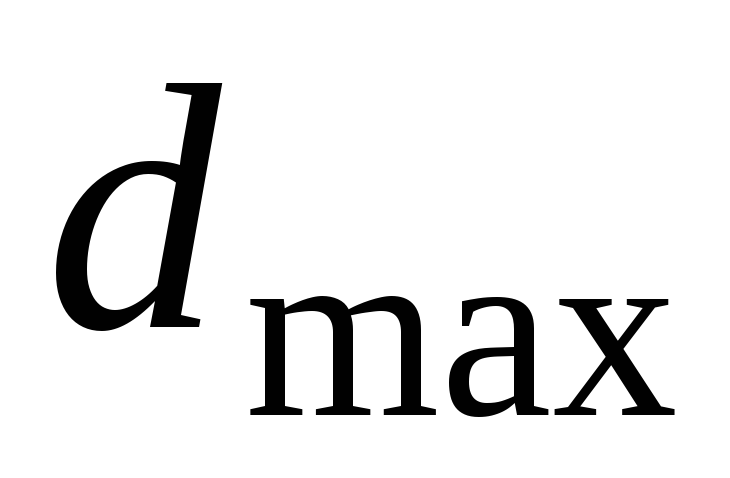6. Вычисляется эмпирическое значение критерия :

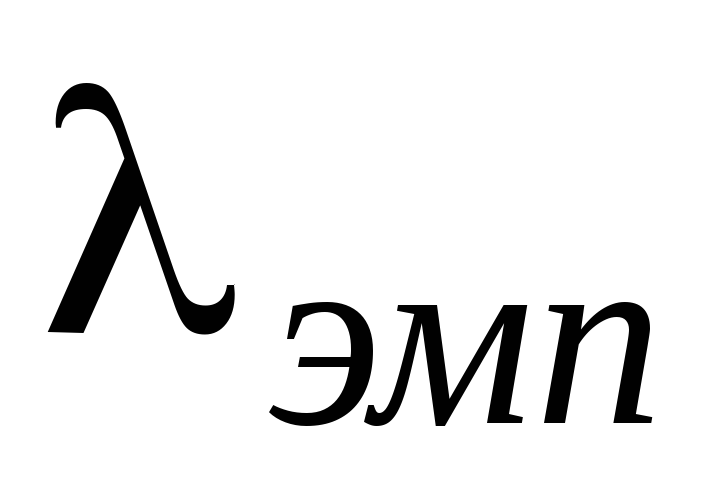7. Определяется критическое значение критерия для выбранного уровня значимости.

8. Если эмпирическое значение критерия больше критического, то нулевая гипотеза отвергается, и группы по рассмотренному признаку отличаются существенно.

Схематично алгоритм применения критерия Колмогорова-Смирнова можно представить следующим образом:

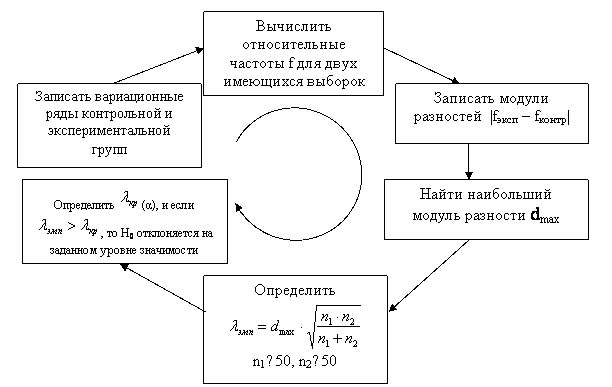
Пример сравнения двух независимых выборок с использованием теста Колмогорова-Смирнова

Являются ли значимыми различия между творческой активностью контрольной и экспериментальной группами студентов?

Уровень усвоения	Частота в экспериментальной группе	Частота в контрольной группе
Хороший	172 чел.	120 чел.
Приблизительный	36 чел.	49 чел.
Плохой	15 чел.	36 чел.
Объём выборки	=172+36+15=223	=120+49+36=205

Вычисляем относительные частоты , равные частному от деления частот на объём выборки, для каждой из имеющихся выборок.

Определяем модуль разности соответствующих относительных частот для контрольной и экспериментальной выборок.

В результате исходная таблица примет следующий вид:

Относительная частота экспериментальной группы (fэксп)	Относительная частота контрольной группы (fконтр)	Модуль разности частот |fэксп – fконтр|
172/223≈0.77	120/205≈0.59	0.18
36/223≈0.16	49/205≈0.24	0.08
15/223≈0.07	36/205≈0.17	0.1

Среди полученных модулей разностей относительных частот выбираем наибольший модуль, который обозначается =0.18.

Эмпирическое значение критерия λэмп определяется с помощью формулы:

Считая, что , по таблице (приложение 4) определяем критическое значение критерия: . , следовательно, нулевая гипотеза отвергается, и группы по рассмотренному признаку отличаются существенно.

5.6 Сравнение двух зависимых выборок

Имеются данные обследования, полученные в двух опытах (или в двух замерах), но на одной и той же группе единиц совокупности. Две выборки считаются зависимыми, если каждому значению одной выборки однозначно ставится в соответствие ровно одно значение другой выборки.

Зависимые (связанные, попарно сопряженные) выборки - это выборки, представляющие собой параметры одной и той же совокупности до и после воздействия некоторого фактора.

Чаще всего зависимые выборки – это измерения одной и той же группы объектов в разные моменты времени (например, до и после воздействия какого-либо фактора). Таким образом, зависимые выборки всегда должны содержать одинаковое количество наблюдений. Для того чтобы доказать эффективность воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Сдвигом называется разность между значениями измеряемого параметра «после» и «до» проведения эксперимента.

Наиболее часто для сравнения зависимых выборок используют параметрический тест – -критерий Стьюдента и непараметрические тесты – критерий знаков и критерий Уилкоксона.

Критерий знаков - это непараметрический тест, использующийся фактически для сравнения медианы распределения с каждым конкретным значением. Критерий знаков предъявляет к тестируемой выборке только одно требование: шкала измерений должна быть порядковой, интервальной или относительной (т.е. тест нельзя применять к номинальным переменным). Других ограничений (в том числе и на форму распределения) нет. С одной стороны, это делает тест настолько широко применимым, насколько это вообще возможно. С другой - снижает его мощность, поскольку тест не может опираться в своей работе на какие-либо предположения о свойствах анализируемого распределения.

Невысокая мощность критерия знаков особенно сильно проявляется на небольших выборках. Это является следствием того, что тест использует информацию только о положении элементов выборки относительно предполагаемой медианы: слева или справа. Информация об их сравнительной величине тестом не используется. В то же время, есть более мощный тест - W-критерий Уилкоксона, использующий информацию о ранге элементов в выборке. К сожалению, сфера применения этого теста ограничена распределениями, симметричными относительно медианы. Для несимметричных распределений он дает некорректные результаты, так что в нашем распоряжении остается только менее мощный критерий знаков.