5.7.2 Сравнение нескольких зависимых выборок. Критерий Фридмана

Критерий Фридмана является непараметрическим аналогом однофакторного дисперсионного анализа для повторных измерений. Он позволяет проверять гипотезы о различии более чем двух повторных измерений по уровню выраженности изучаемой переменной. Критерий более эффективен, чем дисперсионный анализ в случае малых выборок и распределений, отличных от нормального. Он основан на ранжировании повторных измерений для каждого объекта выборки. Проверяется при помощи критерия . Критерий применяется для сопоставления показателей, измеренных в разных условиях () на одной и той же выборке изиспытуемых. Критерий Фридмана позволяет установить, что величины показателей от условия к условию изменяются, но при этом не указывает на направление изменений и в этом смысле он похож на критерий знаков.

Критерий Фридмана является обобщением критерия Вилкоксона на большее, чем два, количество условий измерения, при этом ранжируются не абсолютные величины сдвигов, а сами индивидуальные значения измерений.

Нулевая гипотеза H0={между полученными в разных условиях показателями существуют лишь случайные различия}.

Альтернативная гипотеза H1={между полученными в разных условиях показателями имеются существенные различия}.

Ранжируются индивидуальные значения показателей (повторные измерения) для каждого экземпляра выборки в порядке убывания признака (ранжирование параметров каждой строки).

Полученные ранги суммируются по столбцам (ранги показателей, полученных по всем экземплярам выборки при одних и тех же условиям).

Эмпирическое значение критерия по формуле:

,

где – количество условий (тестов),,– количество экземпляров выборки,,– сумма рангов всех значений при -ом условии.

Критическое значение критерия зависит от уровня значимости α и степени свободы.

Нулевая гипотеза не отвергается, если критическое значение превосходит эмпирическое. В этом случае различия значений показателя в разных условиях можно считать несущественными.

Схема применения критерия имеет вид:

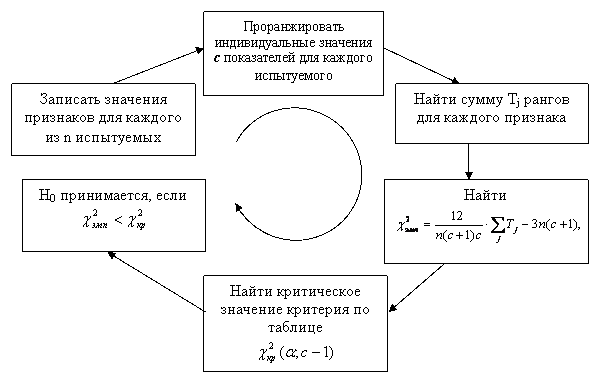
Рис 2 Алгоритм применения критерия Фридмана

Пример использования критерия Фридмана

Пять учащихся исследуются по четырём тестам. Являются ли результаты тестирования случайными?

Таблица 3

	Оценки в баллах по проведённым тестам
Номер испытуемого	Тест A	Тест B	Тест C	Тест D
1	3.6	4.1	2.9	3.5
2	3.8	4.2	3.7	4.6
3	3.3	3.8	3	3.7
4	3.8	3.3	3.4	2.7
5	4	3.6	1.9	3.1

Проранжируем индивидуальные значения показателей для каждого испытуемого в порядке убывания признака. Т.е. производим ранжирование параметров каждой строки представленной таблицы.

Найдём суммы рангов по столбцам. В результате получаем:

Таблица 4

	Ранги тестов (по строкам)
Номер испытуемого	Тест A	Тест B	Тест C	Тест D
1	2	1	4	3
2	3	2	4	1
3	3	1	4	2
4	1	3	2	4
5	1	2	4	3
Сумма рангов:	10	9	18	13

Эмпирическое значение критерия:

Критическое значение критерия , зависит от уровня значимости α и степени свободы. Дляикритическое значение. Нулевая гипотеза не отвергается, так как критическое значение превосходит эмпирическое..