5.7 Сравнение нескольких выборок

Для сравнения нескольких выборок используется:

• дисперсионный анализ для случая нормально распределенных переменных с однородными дисперсиями;

• непараметрические критерии – для распределений, отличных от нормальных и для малых выборок.

Для сравнения более чем двух независимых выборок по уровню выраженности переменных применяется несколько критериев: Н-критерий Крускала (Краскала(-Уоллеса (Уоллиса), критерий медиан, критерий Джонкира-Терспта. Из них наибольшей чувствительностью к различиям обладает критерий Крускала-Уоллиса. Этот критерий является непараметрическим аналогом дисперсионного анализа. Отличия состоят в том, что:

• сравниваются не средние значения переменных, а средние значения их рангов;

• используется не F-критерий Фишера, а критерий хи-квадрат.

Дисперсионный анализ обеспечивает более точные результаты, но условием его применения является нормальное распределение значений признака и однородность дисперсий или достаточно большой размер выборок.

Для малых выборок и распределений, отличающихся от нормальных рекомендуется использовать критерий Крускала-Уоллиса.

5.7.1 Сравнение нескольких независимых выборок. Критерий Крускала-Уоллиса

Критерий Краскела — Уоллиса предназначен для проверки равенства медиан нескольких выборок. Он является обобщением U-критерия Манна-Уитни на случай несвязанных выборок () и предназначен для оценки различий по уровню какого-либо признака одновременно между тремя и более выборками.

Критерий Краскела — Уоллиса является ранговым, поэтому он инвариантен по отношению к любому монотонному преобразованию шкалы измерения.

Нулевая гипотеза H0={между выборками существует лишь случайные различия по уровню исследуемого признака}.

Альтернативная гипотеза Н1={между выборками имеются существенные различия}.

Значения признака ранжируются для всех выборок, как для одной, в порядке возрастания. Далее рассчитывают суммы рангов для каждой выборки отдельно. Выборки могут быть как разных, так и равных объемов.

Эмпирическое значение критерия Крускала-Уоллиса рассчитывается по следующей формуле:

,

где – общее количество испытуемых,– сумма рангов в-ой выборке,– число испытуемых в-ой выборке.

Нулевая гипотеза сдвига отклоняется на уровне значимости , если, где — критическое значение, вычисляемое при (количество выборок) ипо специальным таблицам. При бо́льших значениях применимы различные аппроксимации, например, присправедлива аппроксимация распределения статистики распределениемсо степенями свободы, то есть нулевая гипотеза отклоняется, если.

Схема применения критерия Крускала-Уоллиса выглядит следующим образом

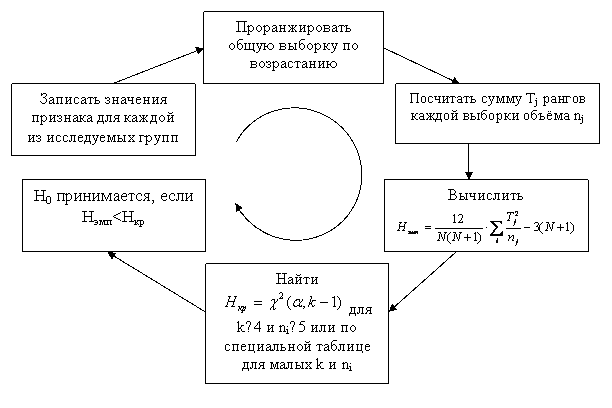
Рис 1 Алгоритм применения критерия Крускала-Уоллиса

Пример использования критерия Крускала-Уоллиса

Одинакова ли степень освоения нового материала младших и старших школьников и учителей.

Таблица 1

	1	2	3	4	5	6	7	8	9
Младшие подростки	2.8	2.8	2.9	3.1	2.9	2.5	2.7	2.8	2.7
Старшие подростки	3.8	3.1	4.0	3.2	3.8	2.5	3.8	2.9	2.8
Учителя	3.7	3.7	2.8	3.9	3.9	3.6	2.6	3.7	2.7

Значения признака ранжируется для всех выборок, как для одной, в порядке возрастания. Далее вычисляются суммы рангов для каждой выборки отдельно (т.е. произведём суммирование рангов по строкам, см. таблицу).

Таблица 2

	1	2	3	4	5	6	7	8	9	Сумма рангов
Младшие подростки	2.8	2.8	2.9	3.1	2.9	2.5	2.7	2.8	2.7	-
Ранг (мл.подростков)	9	9	13	15.5	13	1.5	5	9	5	80
Старшие подростки	3.8	3.1	4.0	3.2	3.8	2.5	3.8	2.9	2.8	-
Ранг (ст. подростки)	23	15.5	27	17	23	1.5	23	13	9	152
Учителя	3.7	3.7	2.8	3.9	3.9	3.6	2.6	3.7	2.7	-
Ранг (учителя)	20	20	9	25.5	25.5	18	3	20	5	146

Эмпирическое значение критерия:

В рассматриваемом примере количество испытуемых во всех группах одинаково и равно 9. На практике выборки могут быть разных объёмов.

Критическое значение критерия по уровню значимости и степени свободы. При этом степень свободы рассчитывается как разность количества групп и единицы, то есть. Прикритическое значение. В данном случае нулевая гипотеза на уровне значимости 0.05 не отвергается, выборки не имеют существенных отличий по исследуемому признаку.