
- •Лабораторный практикум
- •Электронное издание локального распространения
- •Формульный компилятор
- •1.1. Содержание работы.
- •1.2. Задание по работе.
- •1.3. Варианты заданий.
- •1.4. Методические указания.
- •1.5. Контрольные вопросы.
- •Стохастические сетевые модели вычислительных процессов
- •2.1. Содержание работы.
- •2.2. Задание по работе.
- •2.3. Варианты заданий.
- •2.4. Методические указания.
- •2.4.1. Расчёт характеристик разомкнутой сети.
- •2.4.2. Расчёт характеристик замкнутой сети смо.
- •2.4.2.1. Вычисление нормирующего множителя.
- •2.5. Содержание отчёта
- •2.6. Контрольные вопросы
- •Исследование сетей Петри
- •3.1. Содержание работы
- •3.2. Задание по работе
- •3.3. Варианты заданий
- •3.4. Методические указания
- •3.5. Содержание отчёта
- •4.2. Задание по работе.
- •4.3. Задание по уир.
- •4.4. Варианты заданий.
- •4.5. Методические указания.
- •4.6. Содержание отчёта.
- •4.7. Контрольные вопросы.
2.4.2. Расчёт характеристик замкнутой сети смо.
Расчёт замкнутых сетей значительно сложнее. Поскольку система уравнений (5.1) в этом случае приобретает множество решений и интенсивности потоков заявок в сети найти, непосредственно не удаётся.
Наиболее наглядным способом расчёта характеристик является параметрический способ, но он очень громоздок и поэтому применяется относительно редко. Наиболее эффективно можно рассчитать замкнутую сеть через определение маргинальных распределений с помощью нормирующих множителей, что и будет рассмотрено в данной лабораторной работе.
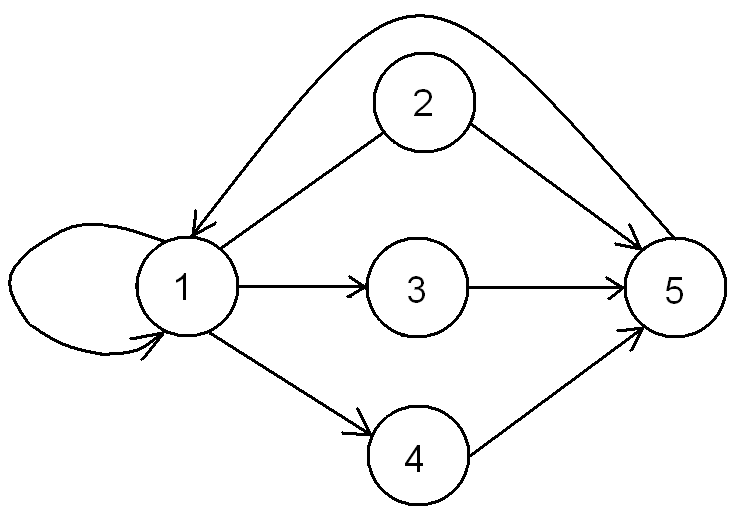
Рис. 2.2. Замкнутая экспоненциальная сеть.
Маргинальное распределение - это распределение числа заявок в отдельной СМО сети. Зная его, можно вычислить и все прочие характеристики сети.
Маргинальное распределение Pj(m)в узлеjопределяется как
Pj (m) = ρm j G(N-j, M-m)/G(N, M)(2.12)
где: ρ - условный коэффициент загрузки СМО j,
G(N-j, M-m)- нормирующий множитель для сетевой модели, в которой отсутствует СМО j и обслуживается M-m заявок,
G(N, M)- нормирующий множитель для сети, содержащей N СМО и обслуживающей M заявок.
2.4.2.1. Вычисление нормирующего множителя.
Для вычисления нормирующего множителя известно несколько принципиально различных способов. Рассмотрим наиболее эффективный, основанный на двухпараметрической рекурсии.
Формула двухпараметрической рекурсии имеет вид:
G(N, M) = G(N-j, M) + ρj*G(N, M-1) (2.13)
Чтобы воспользоваться этой двухпараметрической рекурсивной формулой, необходимо заполнить таблицу значений различных нормирующих множителей меньшего порядка.
Таблица 2.1. Схема вычисления нормирующего множителя.
|
G(N,1) |
G(N,2) |
G(N,3) |
. . . |
G(N,M) |
|
|
G(N-1,2) |
G(N-1,3) |
. . . |
G(N-1,M) |
|
. . . |
. . . |
. . . |
. . . |
. . . |
|
|
G(2,2) |
G(2,3) |
. . . |
G(2,M) |
|
G(1,1) |
G(1,2) |
G(1,3) |
. . . |
G(1,M) |
Таблица 2.1 состоит из нормирующих множителей меньшей размерности, чем заданный нормирующий множитель G(N,M). Левый столбец и нижняя строка таблицы образованы краевыми значениями нормирующих множителей.
Для вычисления краевых значений рекурсивная формула не требуется.
Так,
G(N, 1) =Σ ρj , (2.14)
и
G(1, M) = ρM (2.15)
Краевые значения позволяют применить формулу двух параметрической рекурсии сначала для вычисления второй снизу строки, а затем и всех прочих строк. Таким образом, для вычисления нормирующего множителя необходимо всякий раз вычислять всю таблицу 1 целиком.
При нахождении нормирующих множителей используется всякий раз условное значение коэффициента загрузки, которое находится как отношение
ρ = λ/μ. (2.16)
Значения λ находятся из системы (2.1) при условии λ1=1.
Безусловные значения коэффициентов загрузок находятся на основании вероятностного свойства коэффициента загрузки : коэффициент загрузки - это вероятность наличия хотя бы одной заявки в СМО. Поэтому, вычислив маргинальные распределения Pj (m), мы находим истинные значения коэффициентов загрузок как сумму вероятностей:
![]() (2.17)
(2.17)
Вычислив все безусловные коэффициенты загрузок, убеждаемся, что в замкнутой сети они всегда меньше единицы. Теперь можно вычислить истинное значение интенсивностей потоков заявок, действующих в замкнутой сети из уравнения расхода:
λj = ρj*μj (2.18)
Здесь возможно выполнение проверки. Найденные значения интенсивностей потоков заявок, должны удовлетворять системе (2.1).
Среднее число заявок в СМО находится из маргинального распределения как математическое ожидание:
![]() (2.19)
(2.19)
З десь
также возможно выполнение проверки:
сумма всех средних значений m должна
быть равна заданному числу заявок в
замкнутой сети.
десь
также возможно выполнение проверки:
сумма всех средних значений m должна
быть равна заданному числу заявок в
замкнутой сети.
Средняя длина очереди находится из простого соотношения:
Lj = mj - ρj (2.20)
Среднее время пребывания и среднее время ожидания находятся аналогично как и в разомкнутой сети по формулам (2.5-6).
При определении сетевых характеристик, следует иметь в виду, что коэффициенты передач в замкнутой сети имеют несколько другой смысл. А именно, они показывают сколько раз заявка побывает в СМО j прежде, чем она вернётся в СМО 1, которая является точкой отсчёта. В силу произвола нумерации СМО, значения коэффициентов передач в замкнутой сети относительны и вычисляются по формуле:
αj = λj /λ1 (2.21)
Во всём остальном сетевые характеристики рассчитываются аналогично расчёту сетевых характеристик для разомкнутой сети.
При расчёте характеристик замкнутой сети необходимо воспользоваться подпрограммой решения линейной системы алгебраических уравнений, полученной при расчёте характеристик разомкнутой сети. В дальнейшем рекомендуется применить двух параметрический алгоритм и рассчитать сразу же маргинальные распределения через нормирующие множители. Маргинальные распределения позволят легко найти и все прочие характеристики замкнутой сети.




 G(N-1,1)
G(N-1,1)




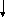 G(2,1)
G(2,1)