Найпростішою формулою, що відтворює тенденцію розвитку, є лінійна функція:

(2.68)

Параметри та 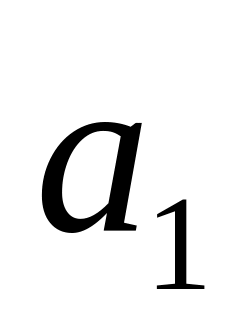згідно методу найменших квадратів знаходяться рішенням системи нормальних рівнянь:

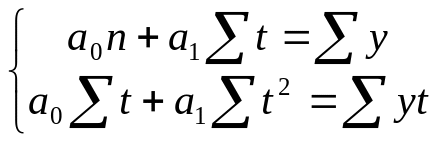, (2.69)

де y – фактичні рівні ряду

t – порядковий номер періоду або моменту часу.

Розрахунок параметрів значно спрощується, якщо за початок відліку часу (t = 0) обрати центральний інтервал. Значення умовних періодів t залежать від того, парну чи непарну кількість рівнів має динамічний ряд.

Якщо число рівнів парне (наприклад, 6), умовні періоди мають значення, наведені в табл. 2.7.

Таблиця 2.7

Значення параметра t у разі введення умовного нуля для парної кількості рівнів динамічного ряду

Фактичний період	1	2	3	4	5	6
Умовний період	– 5	– 3	– 1	1	3	5

Якщо число рівнів непарне (наприклад 7), умовні періоди мають значення, наведені в табл. 2.8.

Оскільки мета введення умовного нуля – максимальне спрощення розрахунків, то відстані між сусідніми рівнями динамічного ряду з умовними періодами мають бути мінімальними, проте однаковими впродовж усього ряду. Таким чином, у разі парної кількості рівнів динамічного ряду відстані між будь-якими двома рівнями з умовними періодами дорівнюють двом; у разі непарної кількості рівнів динамічного ряду відстані між будь-якими двома рівнями з умовними періодами дорівнюють одиниці. Умовні періоди, розташовані ліворуч умовного нуля, набувають від’ємних значень, а ті, що розташовані праворуч – додатних.

Таблиця 2.8

Значення параметра t у разі введення умовного нуля для непарної кількості рівнів динамічного ряду

Фактичний період	1	2	3	4	5	6	7
Умовний період	– 3	– 2	– 1	0	1	2	3

Незалежно від кількості рівнів у динамічному ряді з умовними періодами  t = 0, а тому система нормальних рівнянь для лінійної моделі тренду матиме такий вигляд:

. (2.70)

Тоді параметри а₀таа₁ для лінійної моделі тренду розраховуються за формулами:

(2.71)

Якщо у трендовій моделі використовуються нелінійні функції, то вони приводяться до лінійного вигляду за допомогою певних математичних перетворень [7, 10, 16, 19]. Методика побудови трендових рівнянь за лінійною моделлю та моделлю квадратичної параболи наведена у прикладі 1 розв’язання типових задач до даної теми.

Елементи інтерполяції та екстраполяції на основі часових рядів

Зробити прогноз явища у означає обчислити значення ознаки Yна той майбутній період часу t, який нас цікавить. Очевидно, що будь-який прогноз може бути тільки наближеним і може вважатись реальним тільки за умови збереження у майбутньому тенденції розвитку явища та її характеру. Метод прогнозування на періоди за межами ряду динаміки (на майбутнє або за минулі періоди часу) називають екстраполяцією. Метод прогнозування на періоди пропущених періодів часу в середині ряду динаміки називають інтерполяцією.

Точковий прогноз здійснюється за допомогою екстраполяції трендової моделі, тобто прогнозоване значення явища обчислюється за встановленою формулою. При цьому слід мати на увазі той факт, що рівняння трендової кривої побудоване з використанням умовних періодів, а тому для визначення точкового прогнозу вводиться наступний період. Наприклад, якщо динамічний ряд містить шість періодів, то точкова оцінка розраховується для наступного, сьомого періоду (див. табл. 3.7) якщо динамічний ряд містить сім періодів, то точкова оцінка розраховується для наступного (умовного) четвертого періоду (див. табл. 2.8).

Інтервальний прогноз являє собою інтервал значень ознаки у, який із заданою ймовірністю покриває (або має покривати) справжнє значення:

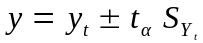, (2.72)

де у_t – точковий прогноз

– довірче число, яке обирається з таблиць розподілу Стьюдента (якщо кількість рівнів динамічного ряду менше 30) або з таблиць нормального розподілу (якщо кількість рівнів динамічного ряду більша за 30)

– залишкове середнє квадратичне відхилення.

Залишкове середнє квадратичне відхилення розраховується за формулою:

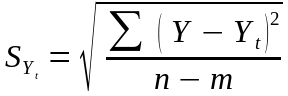, (2.73)

де Y – фактичні рівні досліджуваного динамічного ряду

Y_t – теоретичні значення трендової моделі у відповідні періоди

n – кількість рівнів динамічного ряду

m – число параметрів трендової моделі (для лінійної моделі m = 2).

Такий інтервал називають довірчим інтервалом, а відповідну ймовірність – довірчою ймовірністю.

На відміну від точкового інтервальний прогноз може розроблятися лише на наступний період [7, 10, 16, 19, 21 ].