
- •Університет митної справи та фінансів
- •Міністерство освіти і наукиукраїни
- •Програма навчальної дисципліни «статистика»
- •Зміст навчальної дисципліни «статистика» модуль 1. Теорія статистики
- •Тема 5. Узагальнюючі статистичні показники
- •Тема 6. Методи аналізу рядів розподілу
- •Змістовий модуль 3. Аналіз закономірностей динаміки
- •Тема 7. Аналіз інтенсивності динаміки
- •Тема 8. Виявлення і вимірювання тенденцій розвитку
- •Тема 9. Індексний метод
- •Тема 10. Статистичні методи вивчення взаємозв’язків явищ
- •Тема 11. Вибірковий метод спостереження
- •Тема 1. Методологічні засади статистики
- •Завдання та методичні рекомендації до вивчення теми
- •I етап - Статистичне спостереження
- •II етап - Первинна обробка, зведення, класифікація та групування статистичних даних.
- •Питання для самоконтролю
- •Тестові завдання
- •1. Предметом статистики є вивчення:
- •Тема 2. Статистичне спостереження План вивчення теми
- •Завдання та методичні рекомендації до вивчення теми
- •Програмно-методологічні питання
- •Визначення організаційної форми, виду та способу проведення спостереження
- •Логічний та арифметичний контроль даних
- •Питання для самоконтролю
- •Тестові завдання
- •Проводиться запис шлюбів та розлучень. За ступенем охоплення одиниць сукупності це спостереження:
- •Тема 3. Зведення і групування статистичних даних План вивчення теми
- •Завдання та методичні рекомендації до вивчення теми
- •Графічне зображення результатів групування
- •Побудова вторинних групувань
- •Питання для самоконтролю
- •Приклади розв’язання типових задач
- •Розподіл робітників складального цеху за кваліфікацією
- •Підприємство і
- •Підприємство іі
- •Тестові завдання
- •Тема 4. Подання статистичних даних:таблиці та графіки План вивчення теми
- •Завдання та методичні рекомендації до вивчення теми
- •Питання для самоконтролю
- •Тестові завдання
- •Змістовий модуль 2. Агрегування інформації та аналіз закономірностей розподілу
- •Тема 5. Узагальнюючі статистичні показники План вивчення теми
- •Завдання та методичні рекомендації до вивчення теми
- •Середні величини
- •Питання для самоконтролю
- •Приклади розв’язання типових задач
- •Тестові завдання
- •Тема 6. Методи аналізу рядів розподілу План вивчення теми
- •Завдання та методичні рекомендації до вивчення теми
- •Вимірювання варіації ознак за допомогою абсолютних і відносних мір варіації: розмаху варіації, середніх лінійного та квадратичного відхилень, коефіцієнтів варіації
- •Показники варіації та формули для їх розрахунку
- •Оцінювання інтенсивності структурних зрушень
- •Аналіз рівномірності розподілу за допомогою коефіцієнтів концентрації та децильної диференціації
- •Характеристики форми розподілу: коефіцієнти асиметрії та ексцесу
- •Питання для самоконтролю
- •Приклади розв’язання типових задач
- •Розподіл товару на складі за його ціною
- •Тестові завдання
- •Длянаведеного ряду розподілу
- •Коефіцієнт Джині дозволяє оцінити:
- •Тема 7. Аналіз інтенсивності динаміки План вивчення теми
- •Завдання та методичні рекомендації до вивчення теми
- •1 Метод – з використанням коефіцієнтів перерахунку.
- •2 Метод - заміна абсолютних рівнів відносними.
- •Абсолютні та відносні характеристики інтенсивності динаміки
- •Розрахунок середнього абсолютного приросту і середнього темпу приросту
- •Оцінка прискорення (уповільнення) розвитку. Порівняльний аналіз динамічних рядів з використанням коефіцієнтів випередження та еластичності
- •Питання для самоконтролю
- •Приклади розв’язання типових задач
- •Результати обчислення показників динамічного ряду
- •Результати приведення до однієї основи показників динамічних рядів
- •Тестові завдання
- •Якщо у 2010 р. На підприємстві обсяг виробленої продукції становив 15 млн. Грн., а у 2014 р. – 20 млн. Грн., то середньорічний абсолютний приріст обсягу продукції за цей період часу становить:
- •Тема 8. Виявлення і вимірювання тенденцій розвитку План вивчення теми
- •Завдання та методичні рекомендації до вивчення теми
- •Застосування ступінчастої та ковзної середніх для згладжування коливних рядів
- •Обґрунтування типу трендового рівняння, інтерпретація параметрів
- •Найпростішою формулою, що відтворює тенденцію розвитку, є лінійна функція:
- •Значення параметра t у разі введення умовного нуля для парної кількості рівнів динамічного ряду
- •Значення параметра t у разі введення умовного нуля для непарної кількості рівнів динамічного ряду
- •Елементи інтерполяції та екстраполяції на основі часових рядів
- •Питання для самоконтролю
- •Приклади розв’язання типових задач
- •1. Метод середньої ступінчастої
- •2. Метод середньої плинної
- •3. Метод аналітичного вирівнювання
- •Допоміжна таблиця для розрахунку параметрів лінійної моделі
- •Значення параметра t у разі введення умовного нуля для непарної кількості рівнів динамічного ряду
- •Допоміжна таблиця для розрахунку параметрів параболи
- •Тестові завдання
- •Тема 9. Індексний метод План вивчення теми
- •Завдання та методичні рекомендації до вивчення теми
- •Суть індексів та їх роль у статистичному аналізі, розрахунок індивідуальних індексів
- •Розрахунок зведених індексів - агрегатних та середньозважених. Вибір форми індексу
- •Розкладання абсолютного приросту результативного показника за факторами
- •Методика розрахунку індивідуальних і зведених (загальних) індексів агрегатної та середньозваженої форм
- •Дослідження динаміки середніх величин
- •Питання для самоконтролю
- •Приклади розв’язання типових задач
- •Тестові завдання
- •Економічний зміст мають індекси ціни:
- •13. Середня геометрична з двох різнозважених індексів – це індекс ціни:
- •Тема 10. Статистичні методи вивчення взаємозв’язків явищ План вивчення теми
- •Завдання та методичні рекомендації до вивчення теми
- •Сутність та види взаємозв’язків явищ. Графічні методи вивчення кореляційного зв’язку
- •Метод аналітичних групувань і дисперсійний аналіз. Оцінювання щільності кореляційного зв’язку за даними аналітичного групування
- •2.Оцінка лінії регресії:
- •Регресійно-кореляційний аналіз взаємозв’язку. Оцінювання щільності та перевірка істотності кореляційного зв’язку на основі рівняння регресії
- •Питання для самоконтролю
- •Приклади розв’язання типових задач
- •Залежність між факторною (х) та результативною (у) ознаками
- •Допоміжна таблиця для розрахунку параметрів лінійної моделі
- •Допоміжна таблиця для обчислення коефіцієнта кореляції Пірсона
- •Тестові завдання
- •Тема 11. Вибірковий метод спостереження План вивчення теми
- •Оцінювання точності вибіркових даних. Розрахунок стандартної похибки вибірки і побудова довірчих меж для середньої і частки
- •Визначення мінімально достатнього обсягу вибірки
- •Питання для самоконтролю
- •Приклади розв’язання типових задач
- •Розподіл проданого товару за цінами
- •Дискретний ряд розподілу проданого товару за цінами
- •Розподіл засуджених за віком за звітний період (дані умовні)
- •Тестові завдання
- •Тема 3:Зведення і групування статистичних даних
- •Методичні рекомендації
- •Задачі для розв’язання Задача 1
- •Задача 2
- •Задача 3
- •Завдання 4
- •Завдання 5
- •Завдання6
- •Задача 7
- •Задача 8
- •Практичне заняття №2
- •Тема 5:Узагальнюючі статистичні показники План заняття
- •Методичні рекомендації до практичного заняття Розрахунок різних видів абсолютних і відносних величин, їх аналіз
- •Задачі для розв’язання Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Задача 7
- •Задача 8
- •Задача 9
- •Практичне заняття №3
- •Тема 6:Методи аналізу рядів розподілу План заняття
- •Методичні рекомендації до практичного заняття
- •Задачі для розв’язання Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Задача 7
- •Практичне заняття №4
- •Тема7: Аналіз інтенсивності динаміки План заняття
- •Методичні рекомендації до практичного заняття
- •Задачі для розв’язання Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача5
- •4. Індивідуальні завдання та методичні рекомендації до їх виконання
- •Рекомендації до вибору теми із
- •Основні етапи виконання із
- •5. КонтрольнІ заходи
- •Вимоги до оформлення ккр
- •Перелік питань для підготовки до класної контрольної роботи
- •Перелік питань для підготовки до іспиту
- •Література
- •Internet-ресурси:
- •Додатки
- •Значення критерію Стьюдента
- •Статистика
Середні величини
Однією з узагальнюючих характеристик в аналізі суспільних явищ є середня величина. Середня узагальнює весь діапазон даних і є результатом абстрагування відмінностей, що притаманні одиницям сукупності. Середні величини - це узагальнююча міра варіативної ознаки у статистичній сукупності; це узагальнюючий показник, який характеризує типовий рівень ознаки, що варіює, в розрахунку на одиницю сукупності.
Основні умови наукового використання середніх величин:
якісна однорідність сукупності;
сукупність має бути достатньо великою.
Критерій правильного вибору форми середньої величини - це запис логічної формули розрахунку осереднюваного показника. Для кожної середньої є лише одне правильне співвідношення, для реалізації якого залежно від даних, що існують, можна використовувати різні форми середніх: середню арифметичну, середню гармонічну, середню квадратичну, середню геометричну за не згрупованими (просту) і за згрупованими даними (зважену).
Використання кожного виду середніх залежить від двох обставин: по-перше, від характеру індивідуальних значень ознаки (прямі, обернені, квадратичні, відносні); по-друге, від характеру алгебраїчного зв’язку між індивідуальними значеннями ознаки та її загальним обсягом (сума, добуток, степень, квадратичний корінь).
Середня арифметична – використовується для усереднення прямих значень ознак шляхом їх підсумовування. Якщо дані не згруповані:
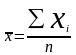 , (2.4)
, (2.4)
де
 - варіанти, тобто значення ознаки, що
осереднюється для i-
ої одиниці сукупності;
- варіанти, тобто значення ознаки, що
осереднюється для i-
ої одиниці сукупності;
n – число одиниць у сукупності.
За формулою середньої арифметичної простої обчислюються також середні у хронологічному ряді, якщо інтервали часу, за який подаються значення ознак, рівні. Якщо у хронологічному ряді наведені моментні показники, то для обчислення середньої вони замінюються півсумами значень на початок і кінець періоду. Якщо моментів більше двох і інтервали між ними рівні, то середня обчислюється за формулою середньої хронологічної:

 (2.5)
(2.5)
де n– число моментів.
Якщо дані згруповані, то використовують середню арифметичну зважену, яку розраховують за формулою:
 , або
, або
 , (2.6)
, (2.6)
де
 - частота;
- частота;
 –
частка
–
частка
 -ї
групи.
-ї
групи.
При цьому

а
 .
(2.7)
.
(2.7)
Середня гармонічна використовується для осереднення обернених індивідуальних значень ознак шляхом їх підсумовування. Для не згрупованих даних це середня гармонічна проста
 . (2.8)
. (2.8)
Якщо дані згруповані, то використовують середню гармонічну зважену
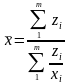 , (2.9)
, (2.9)
де
 - обсяг значень ознаки, тобто.
- обсяг значень ознаки, тобто.
 .
.
Очевидно, що середню гармонічну зважену доцільно використовувати, коли відсутня інформація про значення знаменника логічної формули, тобто відсутні ваги у явному виді.
Середня
геометрична
визначається як добуток відносних
величин динаміки
 ,
які є кратним співвідношенням
,
які є кратним співвідношенням
 -го
значення показника до попереднього
(
-1).
Формула середньої
геометричної простої
-го
значення показника до попереднього
(
-1).
Формула середньої
геометричної простої
 , (2.10)
, (2.10)
де
 -
символ добутку;
-
символ добутку;
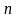 -
кількість величин, середня яких
обчислюється.
-
кількість величин, середня яких
обчислюється.
Якщо часові інтервали неоднакові, використовують середню геометричну зважену
 , (2.11)
, (2.11)
де
 - часовий інтервал.
- часовий інтервал.
У інтервальних рядах, припускаючи рівномірний розподіл у межах -го інтервалу, як варіант використовують середину інтервалу. При цьому ширину відкритого інтервалу умовно вважають такою ж, як і сусіднього закритого інтервалу.
У великих за обсягом сукупностях окремі значення ознаки (варіанти) можуть повторюватись. У такому разі їх можна об’єднати в групи за відповідними варіантами, а обсяг значень ознаки визначити як суму добутків варіант на відповідні їм частоти. Такий процес множення в статистиці називають зважуванням, а число елементів сукупності з однаковими варіантами – вагами. Сама назва “ваги” відображує факт різновагомості окремих варіант. У такому випадку значення ознаки осереднюється за формулою середньої арифметичної зваженої і обчислюється за формулою 2.6.
Для інтервального варіаційного ряду середню арифметичну обчислюють за формулою:
 (2.12)
(2.12)
де
 і
– середина відповідного інтервалу
і
– середина відповідного інтервалу
fi – частота відповідного інтервалу.
У статистиці використовується припущення, що в межах інтервалу варіанти підпорядковуються рівномірному закону розподілу. Це припущення дає можливість під час розрахунку середньої арифметичної використовувати середини інтервалів. Звичайно, при цьому розрахунок середньої набуває дещо умовного характеру, оскільки у разі відхилення від рівномірного розподілу середня інтервального ряду є менш точною, ніж середня, яка обчислена на основі первинних даних. Середнє значення інтервалу розраховується за формулою:
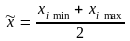 ,
(2.13)
,
(2.13)
де х і min – нижня межа інтервалу
х і max – верхня межа інтервалу.
Для визначення середини відкритого інтервалу приймають припущення, що ширина відкритого інтервалу дорівнює ширині сусіднього інтервалу. Таким чином, немає проблем з визначенням верхньої межі останнього інтервалу. Проте під час визначення нижньої межі першого інтервалу, крім загальної рекомендації, слід ураховувати якісну сутність ознаки, середня якої обчислюється. Наприклад, якщо за загальними рекомендаціями при визначенні нижньої межі отримується від’ємне значення ознаки, варто проаналізувати, чи може ця ознака мати від’ємне значення. Якщо так, нижню межу визначають за загальними рекомендаціями. Якщо ні, за нижню межу обирають нульове значення ознаки.
Слід добре розібрати основні математичні властивості, які має середня арифметична. Однією із таких властивостей є така:
Алгебраїчна сума відхилень кожної варіанти від середньої арифметичної дорівнює нулю. Математично це записується таким чином:
(х
і
–
 )
= 0. (2.14)
)
= 0. (2.14)
Ця властивість використовується при визначенні характеристик варіації – середнього лінійного та середнього квадратичного відхилень (див. методичні рекомендації до наступної теми).
