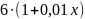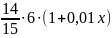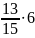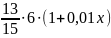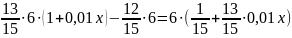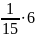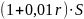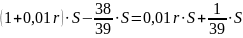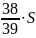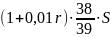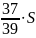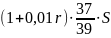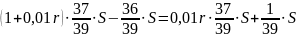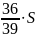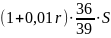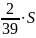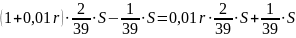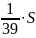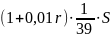- •Задание № 17. ( с 5 )
- •Задачи на сложные проценты:
- •I тип задач: на какой минимальный срок взят кредит.
- •1) Остаток после первого погашения.
- •4. В июле планируется взять кредит в банке на сумму 6 млн. Рублей на некоторый срок. Условия его возврата таковы:
- •5. В июле планируется взять кредит на сумму 20 млн. Рублей на некоторый срок ( целое число лет). Условия его возврата таковы:
- •7. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере
- •II тип задач: под какой процент был взят кредит.
- •9. В июле планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:
- •10. В июле планируется взять кредит в банке на сумму 6 млн. Рублей на срок 15 лет. Условия его возврата таковы:
- •III тип задач: какую сумму взяли в кредит или сумма выплат по кредиту.
- •13. В июле планируется взять кредит в банке на сумму 10 млн. Рублей на 5 лет. Условия его возврата таковы:
- •Задачи на нахождение наибольшего или наименьшего значения.
- •Задание № 17.
- •I тип задач: на какой минимальный срок взят кредит.
- •II тип задач: под какой процент был взят кредит.
- •III тип задач: какую сумму взяли в кредит или сумма выплат по кредиту.
- •Задачи на нахождение наибольшего или наименьшего значения.
7. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере
5
%, затем 12 %, потом
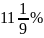 и, наконец, 12,5 % в месяц. Известно, что
под действием каждой новой процентной
ставки вклад находился целое число
месяцев, а по истечении срока хранения
первоначальная сумма вклада увеличилась
на
и, наконец, 12,5 % в месяц. Известно, что
под действием каждой новой процентной
ставки вклад находился целое число
месяцев, а по истечении срока хранения
первоначальная сумма вклада увеличилась
на
 .
Определите срок хранения вклада.
.
Определите срок хранения вклада.
Решение:
Пусть
х рублей
был первоначальный вклад (100 %), по
истечении срока хранения первоначальная
сумма вклада увеличилась на
,
то есть стала
 от х
или
от х
или
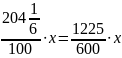 .
.
По
условию задачи,за время хранения вклада
в банке проценты по нему начислялись
ежемесячно сначала в размере 5 %, затем
12 %, потом
и, наконец, 12,5 % в месяц. Обозначим
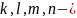 целое число месяцев, соответствующей
процентной ставки.
целое число месяцев, соответствующей
процентной ставки.
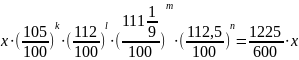
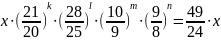
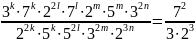
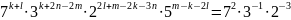

Из
первого уравнения системы получаем,
что
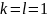 .
Из последнего уравнения системы получаем
.
Из последнего уравнения системы получаем
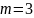 ,
тогда
,
тогда
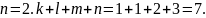
Ответ: 7 месяцев.
II тип задач: под какой процент был взят кредит.
8. 31 декабря 2014 года Борис взял в банке 1 млн. рублей в кредит. Схема выплаты следующая: 31 декабря каждого следующего года банк начисляет процент на оставшуюся сумму долга ( то есть увеличивает долг на определенное количество процентов), затем Борис переводит очередной транш. Борис выплатил кредит за два транша, переведя в первый раз 560 тыс. рублей, а во второй 644, 1 тыс. рублей. Под какой процент банк выдал кредит Борису?
Решение:
Пусть
банк выдал кредит Борису под х%
= 0,01х, тогда
после начисления процентов Борис будет
должен банку
 .
После перевода первого транша сумма
его долга станет
.
После перевода первого транша сумма
его долга станет
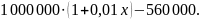 После перевода второго транша сумма
долга будет равна нулю, тогда составляем
уравнение:
После перевода второго транша сумма
долга будет равна нулю, тогда составляем
уравнение:



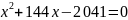
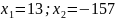 -
не удовлетворяет условию задачи.
-
не удовлетворяет условию задачи.
Ответ: 13 %
июнь 2015
9. В июле планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на a% по сравнения с концом предыдущего года; - февраля по июнь каждого года необходимо выплатить часть долга. Найдите число a, если известно, что кредит был полностью погашен за два года, причём в первый год было переведено 55 000 рублей, а во второй год 69 000 рублей?
Решение:
Пусть
банк выдал кредит под a%
= 0,01a,
тогда после
начисления процентов долг банку будет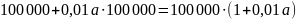 .
После перевода первого транша сумма
его долга станет
.
После перевода первого транша сумма
его долга станет
 После перевода второго транша сумма
долга будет равна нулю, тогда составляем
уравнение:
После перевода второго транша сумма
долга будет равна нулю, тогда составляем
уравнение:
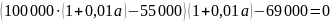
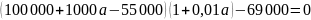
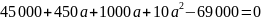

 -
не удовлетворяет условию задачи.
-
не удовлетворяет условию задачи.
Ответ: 15 %
июнь 2015
10. В июле планируется взять кредит в банке на сумму 6 млн. Рублей на срок 15 лет. Условия его возврата таковы:
- каждый январь долг возрастает на x% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга; - в июле каждого года долг должен быть на одну и ту же величину меньше долга за июль предыдущего года. Найти х, если известно, что наибольший годовой платёж по кредиту составит не более 1,9 млн. рублей, а наименьший - не менее 0,5 млн. рублей?
Решение:
Срок |
Кредит |
Долг |
Выплаты
|
1 |
6 |
|
|
2 |
|
|
|
3 |
|
|
|
... |
|
|
... |
15 |
|
|
|
По условию задачи: наибольший годовой платёж по кредиту составит не более 1,9 млн. рублей, а наименьший - не менее 0,5 млн. рублей.

Ответ: 25 %
июнь 2015
11. 15 - го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы: - 1 - го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число месяца необходимо выплатить часть долга; - 15 - го числа каждого месяца долг должен на одну и ту же сумму меньше долга на 15 - е число предыдущего месяца. Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит. Найти r.
Решение:
Iспособ:
Пусть первоначальная сумма кредита S.
Срок |
Кредит |
Долг |
Выплаты |
1 |
S |
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
.... |
... |
... |
.... |
38 |
|
|
|
39 |
|
|
|
40 |
0 |
0 |
0 |
Сумма всех выплат составит:


Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит, тогда
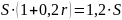

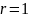
или ( по формулам арифметической прогрессии )
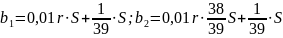
тогда
найдем разность прогрессии
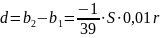
Найдём сумму выплат по формуле суммы n - первых членов арифметической прогрессии


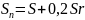
Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит, тогда
Ответ: 1%
II
способ: Пусть
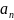 -
сумма долга в конце n
- го месяца,
-
сумма долга в конце n
- го месяца,
 - первоначальная сумма долга.
- первоначальная сумма долга.
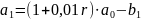
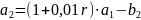
 ,
где
,
где
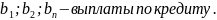
По
условию задачи: сумма долга уменьшалась
равномерно, то есть на одну и ту же
величину каждый месяц, тогда составляет
арифметическую прогрессию, где
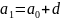
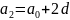
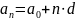 -формула n-
го члена прогрессии.
-формула n-
го члена прогрессии.
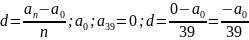
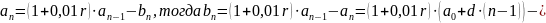

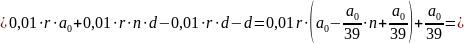
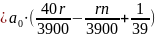
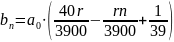
Суммы
выплат составляют арифметическую
прогрессию.


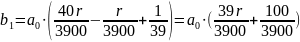
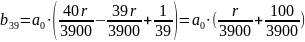
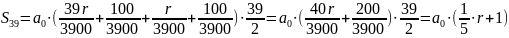
Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит, тогда
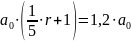
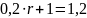
Ответ: 1%
III способ:Укажем общие формулы для решения задач этого типа. Пусть на n платежных периодов (дней, месяцев, лет) в кредит взята сумма S, причём каждый платежный период долг сначала возрастёт на r% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же сумму меньше долга на конец предыдущего платежного периода. Тогда величина переплаты П и полная величина выплат В за всё время выплаты кредита даются формулами
По
условию задачи
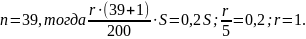
Ответ: 1 %
аналогичные задания:
- 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.
Ответ: 3 %
- Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.
Ответ: 2 %.
- Алексей взял кредит в банке на срок 17 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 27 % больше, чем сумма, взятая им в кредит. Найдите r.
Ответ: 3 %.
12. 15 - го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
Долг ( в % от кредита) |
100 % |
90 % |
80 % |
70 % |
60 % |
50 % |
40 % |
В конце каждого месяца, начиная с января, текущий долг увеличивается на 5 %, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Решение:
Пусть
15 - го числа текущего месяца долг равен
х
рублей, а 15 го числа предыдущего месяца
у
рублей. Тогда в конце предыдущего месяца
долг равен
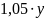 и выплата в первой половине текущего
месяца равна
и выплата в первой половине текущего
месяца равна .
В процентах отсуммы кредита выплаты
в феврале составили
.
В процентах отсуммы кредита выплаты
в феврале составили
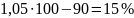 ; в марте
; в марте
 в июне
в июне

Общая сумма выплат составила 15 + 14,5 + 14 + 13,5 + 13 + 52,5 = 122,5 %.
Ответ: 22,5 %