Методички для олимпийцев / Метод жесткостей

Метод жесткостей

Способность деформироваться конструкции (системы) в целом или отдельных ее частей и элементов характеризуется ее постоянными параметрами — жесткостями [1]. В инженерной практике их часто называют коэффициентами жесткости или податливости (величины, обратные жесткостям). Для линейно-упругих систем жесткость не зависит от внешних нагрузок и определяется только свойствами системы (ее материалом, геометрическими размерами и характеристиками поперечных сечений и т.д.). В расчетных формулах они служат связующими элементами между силовыми и деформационными параметрами, которые являются переменными (зависимыми) от внешнего нагружения и других воздействий на систему. Так, для связи напряжения с деформацией в законе Гука, например, в виде в качестве параметра жесткости содержится модуль упругости Е. В зависимостях , , связь производных перемещений осевой линии бруса с внутренними силовыми факторами осуществляется параметрами жесткости EА, EJ_X, GJ_p — жесткостями сечения соответственно на растяжение-сжатие, изгиб и кручение. Внешние нагрузки с линейными и угловыми перемещениями элементов конструкции связаны через соответствующие жесткости конструкции и ее элементов, которые могут быть найдены любым методом сопротивления материалов для определения перемещений, например, интегралами Мора.

Многие задачи, в частности, по определению внутренних силовых факторов в элементах статически неопределимых систем могут быть решены методом жесткостей и весьма эффективно. Но для этого необходимо уметь распознавать последовательное и параллельное соединения (работу) элементов в системе и правильно рассчитывать жесткости как отдельных элементов, так и системы в целом. В связи с эти рассмотрим определение жесткостей системы для этих видов соединения элементов и их комбинации. Расчеты проведем на примерах простейших систем, работающих на растяжение-сжатие. Но полученные окончательные формулы могут быть использованы при любых видах нагружения.

Пример 1. Последовательное соединение элементов (рис.1).

Ступенчатый стержень с заданными характеристиками^- нагружается продольной силой F.

Решение. Применяя метод сечений, находим нормальные силы в поперечных сечениях стержня

(1)

Полное удлинение стержня очевидно равно сумме удлинений отдельных участков, т.е.

(2)

Выразим удлинения через усилия и жесткости стержней:

(3) где — жесткости на растяжение соответственно первой и второй ступеней.

Вводя суммарную жесткость стержня с для концевого сечения, где прикладывается сила F, можем записать, что

(4)

Подставив выражения удлинений (3) и (4) в уравнение (2), получим

,

где — податливости соответственно первого, второго участков и стержня в целом.

Вывод. При последовательном соединении упругих элементов нагрузки во всех элементах — одинаковые. Суммарные жесткость с

податливость δ

где п — число соединенных элементов.

Пример 2. Параллельное соединение элементов (рис. 2, а).

С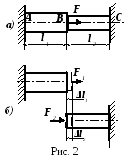тупенчатый стержень с заданными характеристиками защемлен по концам и нагружается продольной силой F.

Решение. Система статически неопределима. Будем ее рассматривать как задачу о нагружении двух стержней, получаемых из исходной разъединением по сечению В (рис.П.2, б). Силу F разделим на две части F ₁ и F ₂ — такие, при которых перемещения сечения приложения силы F ₁ и сечения приложения силы F ₂ будут одинаковыми. Тогда заданная и построенная расчетная схемы эквивалентны. Для решения имеем два уравнения: сил

(5)

и перемещений

(6)

Выразим удлинения через силы и жесткости стержня

(7)

где — жесткости ступеней стержня, с— суммарная жесткость стержня в сечении В.

Подставив выражения (7)в уравнения (5), (6), получим выражения:

для суммарной жесткости с = c ₁+c ₂ ,

для сил, приходящихся на отдельные стержни,

Вывод. При параллельном соединении упругих элементов перемещения сечений в точках приложения нагрузок — одинаковые. Суммарная жесткость системы равна сумме жесткостей ее элементов

Нагрузка распределяется по элементам пропорционально их жесткостям

где с _i — жесткость i-го элемента; п — общее количество элементов

Пример 3. Комбинированное соединение элементов (рис.3).

Д

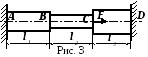Т рехступенчатый стержень с заданными характеристиками защемлен по концам и нагружается продольной силой F.

Решение. При нагружении силой F поперечное сечение С получит горизонтальное перемещение, которое будет общим для участков АС и CD, следовательно, эти участки работают параллельно. Для определения суммарной жесткости с стержня можем использовать формулы, полученные в решении примера 2, т.е. , где с _АС — жесткость участка АС; — жесткость участка CD. Участок АС стержня состоит из ступеней АВ и ВС, которые нагружаются одинаковыми нормальными силами, следовательно, эти ступени работают последовательно. Тогда для определения жесткости c_АС можем применить формулы, полученные в решении примера 1, т.е., где , — жесткости на растяжение первой и второй ступеней стержня.

Таким образом, жесткость стержня в сечении приложения силы F равна

.

Отметим, что зная с можно легко найти, например, перемещение сечения С

работу силы F

При решении задач с использованием метода жесткостей надлежит руководствоваться следующими правилами.

1. Применять для систем, при анализе которых есть полная уверенность в параллельной или последовательной работе ее элементов.

2. Признак параллельно работающих элементов — одинаковые перемещения элементов в точках (сечениях) приложения нагрузок.

3. Признак последовательно работающих элементов — одинаковые нагрузки во всех элементах.

4. Для системы с параллельно работающими элементами:

суммарная жесткость равна сумме жесткостей ее элементов ;

распределение нагрузок по элементам пропорционально их жесткостям

5. Для системы с последовательно работающими элементами:

суммарная податливость равна сумме податливостей ее элементов

нагружение всех элементов — одинаковое .

В заключение покажем эффективность решения некоторых задач с использованием метода жесткостей на следующем примере. Дана рама с квадратным поперечным сечением b х b стержней (рис.4, а), нагруженная силой F. Требуется найти наибольшее напряжение.

Решение. Задача два раза статически неопределима, но методом жесткостей решается буквально устно. Разъединим систему по шарниру и представим в виде, показанном на рис.4, б, где F ₁ + F ₂ = F . Вертикальные перемещения (по направлению сил F ₁ и F ₂) левой части и правой одинаковые, так как они были соединены шарниром. Следовательно, имеем систему, состоящую из двух параллельно работающих элементов. Левый работает на изгиб, а правый — на сжатие. Но жесткость стержней рамы на сжатие с_сж (порядка) несоизмеримо выше, чем на изгиб с_и (порядка ), поэтому на основании правила 4 (распределение нагрузок по элементам пропорционально их жесткостям) сила F ₁ несоизмеримо больше, чем F ₂. Пренебрегая последней, получим .

ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА

1. Несмеянов А.С, Садаков О.С. Сопротивление материалов. Нестандартные задачи и подходы к их решению. — Челябинск: ЧГТУ, 1994.

4