3.3. Теории прочности

Чаще всего оценка прочности материала в опасной точке производится по трем теориям прочности:

I) для пластичных материалов - по теории максимальных касательных напряжений

(3.14)

и теории октаэдрических касательных напряжений (или энергетической)

; (3.15)

2) для хрупких материалов - по обобщенной теории прочности 0.Мора

(3.16)

где ν = σ_вр/σ_вс, [σ] - допускаемое напряжение при растяжении; σ_вр - предел прочности при растяжении; σ_вс - предел прочности при сжатии. Отметим, что теория прочности О.Мора справедлива и для пластичных материалов - в этом случай выражение (3.16) совпадает с (3.14), т.к. ν = σ_Тр/σ_Тс = 1.

Коэффициенты запаса, по текучести и по разрушению определяются так:

; (3.17)

(3.18)

Сравнение прочности элементарных частиц материала, находящихся в том или ином напряженном состоянии, осуществляется путем сопоставления величин эквивалентных напряжений.

Задача 3.10. Сопоставить степень опасности напряжённых состояний а), б), в) - рис.3.10 для одинакового материала.

Задача 3.11. Определить, какое напряженное состояние наиболее опасно (рис.3.11), используя теорию наибольших касательных напряжений.

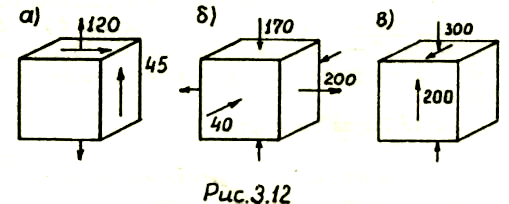Задача 3.12. Для напряженных состояний, изображенных на рис. 3.12 (напряжения даны в МПа), определить коэффициенты запаса: по текучести (рис.3.12, а) - материал сталь, σ_Тр= σ_Тс = 240 МПа и по разрушению (рис.3.12, б,в) - материал ковкий чугун, σ_вр = 500 МПа, σ_вс = 1700 МПа.

Задача 3.13. Для частицы из хрупкого материала (σ_вр = 2·σ_вс) - рис.3.13 найти величину эквивалентного напряжения в функции от параметра п (- ∞< п<+∞).

4. Определение напряжений и расчеты на прочность при простых деформациях бруса

4.1. Формулы для напряжений и условия прочности при растяжении-сжатии, кручении, изгибе бруса постоянного сечения

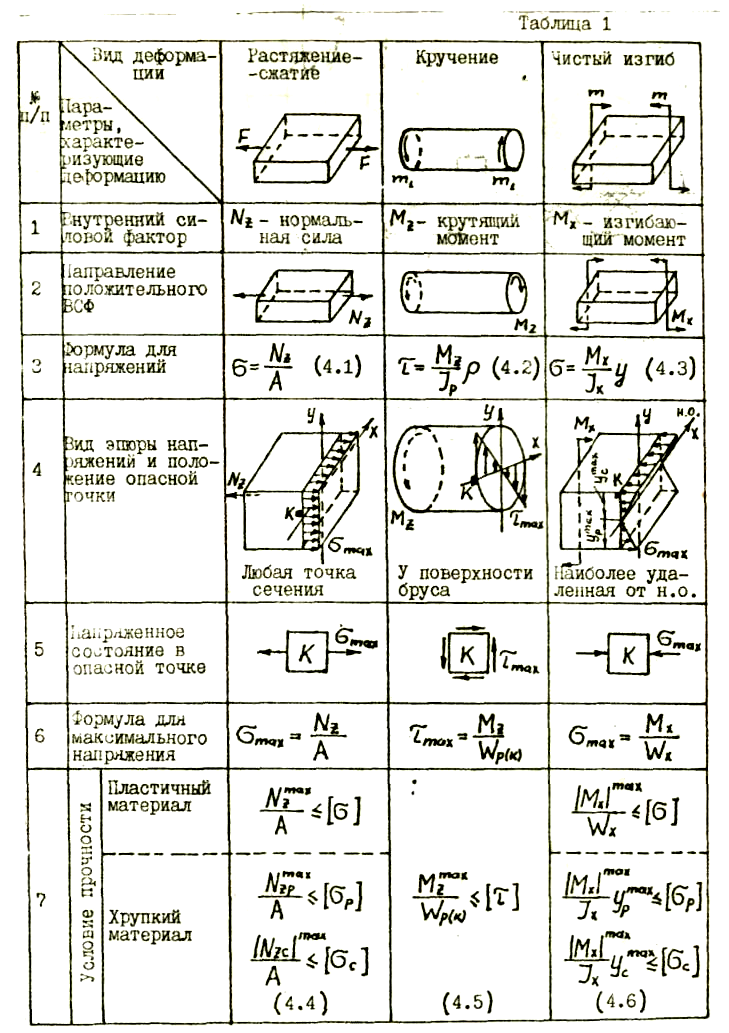
В таблице I представлены основные сведения по расчету брусьев при простых деформациях.

Задача 4.1. а) Определить, какая доля внутреннего силового фактора (ВСФ) (N, М_к, М_x) передается заштрихованной частью поперечного сечения бруса (рис.4.1, а); б) Найти, какая доля N, М_к, М_x передается заштрихованной частью треугольного (рис.4.1, в), прямоугольного (рис.4.1, б) и двутаврового (рис.4.1, г) сечений.

Указание. Отношение долей BCФ, передаваемых частями поперечного сечения, равно отношению жёсткостей этих частей (ЕА, GJ_р , EJ_х).

Задача 4.2. Как изменится прочность бруса квадратного сечения при растяжении, кручении, изгибе, если его из положения а) повернуть в положение б)? (Рис.4.2).

Задача 4.3. При заданных условиях нагружения бруса (рис.4.3, а, б) определить величину допускаемой нагрузки, выбрав рациональное расположение таврового сечения (рис.4.3, в) при изгибе. Известно: l = 1 м, a = 0,04 м, [σ_р] = 60 МПа, [σ_с] = 100 МПа.

Указание. При растяжении-сжатии бруса (рис.4.3,а) опасной является зона сжатия; при изгибе бруса (рис.4.3,б) рациональное расположение тавра определяется максимальным изгибающим моментом в сечении В, а величина допускаемой нагрузки находится из условия прочности по растягивающим напряжениям в сечении С.

Задача 4.4. Найти τтах и построить эпюру касательных напряжений в поперечном сечении балки, работающей на изгиб. Сечение балки имеет форму ромба (рис. 4.4).