3.2. Плоское (пнс) и линейное напряженные состояния (лнс)

ПНС испытывает элементарная частица (рис.3.1, а) в том случае, когда отличны от нуля два главных напряжения; ЛНС имеет место, когда не равно нулю лишь одно главное напряжение из трех.

3.2.1. Основные формулы пнс

На рис.3.5 представлен общий случай плоского напряженного состояния - на передней и задней грани главное напряжение равно нулю, остальные площадки, на которых заданы исходные напряжения (σ_z, σ_у τ_zу, τ_уz,) – не являются главными (по ним действуют касательные напряжения).

Исходные напряжения связаны с относительными (линейными и угловыми деформациями в плоскости уz с помощью закона Гука

, (3.6)

где G - модуль упругости второго рода (модуль сдвига).

Нормальное и касательное напряжения в произвольной площадке, наклоненной к исходной площадке с нормалью z под углом α (рис.3.5), определяются по формулам:

; (3.7)

. (3.8)

Положительными величинами и формулах (3.7) и (3.8) являются растягивающие σ, предающее частицу по часовой стрелке τ_zу и отсчитываемый нротив хода часовой стрелки угол α.

Относительные деформации в произвольном направлении связаны с линейными и угловыми деформациями в плоскости уz (3.6) следующими зависимостями, аналогичными (3.7) и (3.8):

, (3.9)

(3.10)

Отметим, что в случае нагружения частицы или, например, тонкой пластины равномерным давлением q [МПа] в плоскости уz в любой точке и по всем направлениям в этой плоскости возникают одинаковые нормальные напряжения и линейные деформации, т.е.

(3.7,а)

. (3.9,а)

Замечание. Из формул (3.8) и (3.10) следует, что в этом случае касательные напряжения и углы сдвига равны нулю.

3.2.2. Главные площадки и главные напряжения в случае пнс

Положение главных площадок и величина действующих по этим площадкам напряжений определяются по формулам

, (3.11)

, (3.12)

где α₀ - угол наклона главных площадок к исходным; - величина двух главных напряжений, σ₁, σ₂ или σ₃ - индексы проставляются после определения численных значений с учетом, что одно из главных напряжений равно нулю (ПНС) и .

3.2.3. Экспериментальное определение напряжений при пнс

Теоретические зависимости (3.9) и (3.6) дают возможность находить напряжения σ_z, σ_у τ_zу из эксперимента. В опасной точке с помощью специальных приборов (тензометров) устанавливаются относительные деформации но направлению осей , у, n (рис. 3.5 ):

(3.13)

где ΔC_i, Δ₀ - отсчет по шкале и база тензометра, мм; К - коэффициент увеличения тензометра.

По формуле (3.9) вычисляется относительный угол сдвига γ_zy. И, наконец, из выражений (3.6) определяются исходные напряжения в элементарной частице, выделенной вокруг опасной точки.

Задача 3.5. Определить, при каком соотношении между σ_z, σ_y и τ_zy (рис.3.5) напряженное состояние частицы материала будет линейным. Исследовать случаи, когда σ_z > 0, σ_y >0 и σ_z < 0, σ_y < 0.

Указание. В формуле (3.12) приравнять нулю одно из главных напряжений.

Задача 3.6. При заданных условиях нагружения тонких пластин найти нормальные и касательные напряжения по нижней грани (рис.3.6, а) и в сечениях, проведенных по окружности (рис.3.6, б) и по параболе (рис.3.6, в); в двух последних случаях определить точку в сечении, где действует τ_max, и вычислить его величину.

Указание. Для треугольной пластинки записать условие равновесия для проекций всех элементарных сил на вертикаль (рис.3.6, а); для схем на рис.3.6, б, в по исходным напряжениям σ_z, σ_y, значения которых находятся из .условий нагружения пластины, найти σ_α и τ_α, используя выражения (3.7) и (3.8). Положение точки, где действует, определяется исследованием функции τ_α = f(α) на экстремум.

Задача 3.7. Упругие постоянные материала тонкой пластинки (Е, μ) известны. Найти угол α, при котором удлинение элемента АВ равно нулю (рис.3.7).

Указание. По формулам (3.6) находим ε_z, ε_y, а затем из выражения (3.9) определяем угол α, учитывая, что ε_α = 0.

З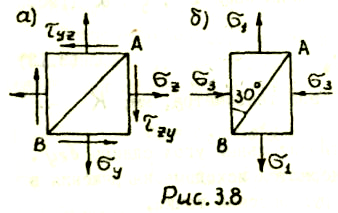адача 3.8. При каком соотношении напряжений, действующих на тонкую квадратную (рис.3.8,а) и прямоугольную (рис.3.8, б) пластинку, длины диагоналей АВ не меняются?

Указание. См. решение предыдущей задачи.

Задача 3.9. При совместном действии на элемент (рис.3.9) растягивающих и сжимающих напряжений показание тензометра составило ΔС = 14 мм. База тензометра Δ₀ = 100 мм, коэффициент увеличения К = 1000. Упругие константы материала - Е = 2·10 ⁵ МПа и μ = 0,3. Каким будет показание тензометра, если с элемента снять растягивающее напряжение?

Указание. По формулам (3.6) находим ε_z, ε_y, а затем из выражения (3.9), определив вначале ε_α (3.13), вычислим величину σ_α. Далее решаем задачу о сжатии элемента напряжением, равным σ_раст.