3. Напряжённо-деформированное состояние. Теории прочности

3.1. Объемное напряженное состояние ( онс )

ОНС имеет место, когда не равны нулю все три главных напряжения (), действующие на элементарную частицу материала (рис.3.1, а). Относительные деформации в направлении главных напряжений определяются по закону Гука

, (3.1)

где Е - модуль упругости первого рода (модуль продольной упругости), μ - коэффициент Пуассона.

В случае всестороннего растяжения или сжатия частицы (и любого тела) давлением q [ МПа ] напряжения в каждой точке тела по всем направлениям одинаковы, т.е.

, (3.1, а)

и . (3.1, б)

Относительное изменение объема

; (3.2)

относительное изменение площади любой грани

где А_1,2 - площадь грани в плоскости действия напряжении σ₁ и σ₂.

При деформации частицы удельная потенциальная энергия: изменения объема

; (3.3)

изменения формы

(3.4)

Максимальное касательное напряжение в частице

, (3.5)

оно действует на площадке, параллельной напряжению σ₂ и наклонённой под углом 45° к напряжениям σ₁ и σ₃.

Для определения главных напряжений при ОНС используют кубическое уравнение вида:

, где

В главных осях напряжений инварианты

Задача 3.1. а) Определить, как изменится объем кубика 1х1х1 см (рис.3.1, б-д), треугольной призмы ахhхl = 1х2x20 см (рис.3.1, е), а для схем на рис.3.1, в-е также и площадь верхней грани при заданных условиях нагружения. Вычислить удельную энергию изменения объема и формы. Известно: F = 10 кН; q - 100 МПа; Е= 2·10⁵ МПа; μ = 0,3; Δ = 1·10^-5 м.

б) Найти, при каком отношении σ₂ /σ₁ и σ₃ /σ₁ кубик (рис.3.1, а) испытывает одноосную деформацию в направлении напряжения σ₁.

в) При каком сочетании составляющих напряженного состояния (рис.3.1, а) удельные потенциальные энергии изменения объема и формы достигают наибольшего и наименьшего значений.

Указание. а) Для схем на рис.3.1, б-д главное напряжение в верхней грани кубика определяется как при простом сжатии; напряжения в других гранях находятся из условий совместности деформаций (ε = 0 или ε = Δ/0,01). Для схемы рис.3.1, е работают выражения (3.1, а, б).

б) В данной задаче (рис.3.1, а) главные напряжения находятся из условия ε₁ = ε₂ = 0.

в) Проанализировать на max и min выражения (3.3) и (3.4), учитывая, .

Задача 3.2. Для заданных цилиндров (рис.3.2, а-г) найти величину давления q и изменение объема, если F = 10 кН; А = 0,001 м²; Е = 2·10⁵ МПа; μ = 0,3; l = I м; дополнительные условия для каждой схемы приведены на рисунке. [σ] = 220 МПа.

Указание. Для схемы рис.3.2, а вначале найти ε_z = - ε_x/μ; для схемы на рис.3.2, б учесть, что ε_z = 0 и ; для схемы на рис.3.2, в учесть, что и ; для схемы на рис.3.2, г имеем .

Задача 3.3. Определить главные напряжения в сечениях стального и медного брусков, вставленных без зазора в жёсткую открытую коробку и нагруженных наружным давлением (рис.3.3). Известно: Е_ст =2 Е_м, μ_ст, μ_М.

У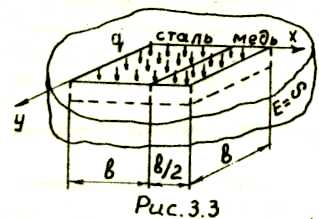казание. Главные напряжения в верхних гранях обоих брусков равны (-q). Одинаковы также и главные напряжения в обоих брусках в направление оси x - величина их не известна. Эту величину и главные напряжения в брусках вдоль оси у найдем, решив три уравнения совместности деформаций:

; ; ,

где ε_i определяется по формулам. (3.1).

Задача 3.4. а) Сравнить изменение объемов шара и куба, изготовленных из одного материала, при нагружении силами F (рис. 3.4, а).

б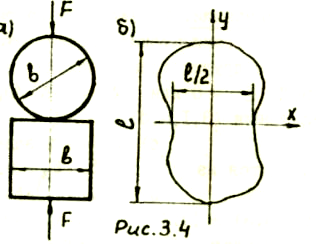) Во сколько раз уменьшение объема тела при нагружении сжимающими силами F в направлении оси у больше, чем при нагружении теми же силами в направлении оси x (рис.3.4,б)?

Указание: Рядом с исходным состоянием нагружения силами F (I) изобразить состояние всестороннего сжатия тела давлением q (II). Далее воспользоваться теоремой о взаимности работ , где ΔV(I) - искомое изменение объема в (I) состоянии, т.е. от действия сил F, а Δl(II)- изменение расстояния между точками приложения сил F во (II) состоянии, т.е. под действием давления q; , где ε_F - относительная деформация в направлении действия сил F при всестороннем сжатии тела, вычисляемая по формулам (3.1,б).