Государственное образовательное учреждение высшего профессионального образования

Московский авиационный институт

(национальный исследовательский университет)

РАДИОВУЗ МАИ

О.М.Данченко

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ

МОСКВА

2012

О.М. ДАНЧЕНКО

Методические указания по выполнению индивидуальных заданий по математическому анализу – М.; РАДИОВТУЗ, 2012г., - 36 с.

Данное пособие содержит типовые задачи для индивидуальных заданий студентов-заочников по курсу «Математический анализ» часть 1. Ко всем задачам приводятся подробные решения и указания. Приведенные задания в равной степени могут использоваться студентами очного отделения при подготовке к экзамену. В приложении приведена подробная программа курса по «Математическому анализу» часть 1.

РАДИОВТУЗ 2012

Содержание

Введение…………………………………………………………………………….

Построение графиков функций, заданных в полярной системе координат или в параметрической форме……………………………………………………………

Вычисление пределов последовательностей и функций…………………………

Исследование функций на непрерывность………………………………………..

Вычисление производных………………………………………………………….

Исследование функций с помощью производных, построение графиков функций……………………………………………………………………………..

Задания на вычисление интегралов……………………………………………….

Приложения…………………………………………………………………………

Введение

В процессе изучения курса «Математический анализ» предусмотрено выполнение студентами индивидуальных домашних заданий в каждом семестре. Индивидуальное домашнее задание 1-ого семестра содержит следующие задачи:

1. Построение графиков функций, заданных в полярной системе координат или заданных в параметрической форме.

2. Вычисление пределов последовательностей и функций.

3. Исследование функций на непрерывность.

4. Вычисление производных от сложных функций, функций, заданных неявно или в параметрической форме.

5. Исследование функций с помощью производных, построение графика функции.

6. Вычисление неопределенного и определенного интегралов.

Рассмотрим далее типовые примеры на каждое из заданий и укажем методы их решения.

Построение графиков функций, заданных в простой полярной системе координат.

Простая полярная система координат характеризуется следующим:

ρ=ρ(φ); 0≤ρ<+∞; 0≤φ≤2π (1)

Положительные углы φ отсчитываются от полярной оси (совпадающей с положительным направлением оси ОХ) против часовой стрелки, отрицательные – по часовой стрелке. При построении графика функции в соответствии с уравнениями (1) следует придерживаться следующего порядка действий:

а) указать область допустимых значений (О.Д.З.), т.е. определить при каких углах φ функция ρ(φ) – неотрицательна, т.е. ρ(φ)≥ 0;

б) найти область изменения функции;

в) указать является ли функция четной или нечетной, т.е. если ρ(-φ) = ρ(φ), то график функции симметричен относительно полярной оси и, следовательно, достаточно сделать исследования для φ≥0. После данных исследований следует построить кривую по точкам.

Пример: построить график функции в простой полярной системе координат ρ=2cos2φ

Так как в простой полярной системе координат ρ≥0, то О.Д.З. будут являться только те углы φ, для которых cos2φ≥0, т.е. 0≤φ≤π/4; 3π/4≤φ≤5π/4; 7π/4≤φ≤2π. Функция будет ограничена, т.к. |cos2φ|≤1, т.е. |2cos2φ|≤2. Так как функция четная и периодическая то достаточно построить кривую только для 0≤φ≤π/4, а затем отразить кривую симметрично относительно полярной оси и в силу периодичности построить аналогичную петлю для 3π/4 ≤φ≤5π/4. Для 0≤φ≤π/4 функция монотонно убывает от двух до нуля, для 3π/4≤φ≤π функция монотонно возрастает от нуля до двух (рис. 1).

Построение графика функции, заданной в параметрической форме.

Пусть x=X(t) и y=Y(t), где параметр t изменяется в определенных заданных пределах. График функции, заданной в параметрической форме, строится по характерным точкам.

Пример: x=t², y= t∙(t²-3)/3

а) Заметим, что для любых значений аргумента t функция x(t)=t²≥0, следовательно, график функции расположен в правой полуплоскости.

б) В силу нечетности функции y(t), так как y(-t)=-y(t), график функции симметричен относительно оси ОХ.

в) Определим точки, в которых y(t) = 0: при t=0, y(0)=0 и x(0)=0

при t= + и t= - y=0, а x(+ ) = 3 – т.е. это точки пересечения графика функции с осью ОХ. Для более точного построения графика функции достаточно добавить еще 2-3 точки, например при t=1 y(1)=-2/3, x(1)=1; при t=2 y(2)=2/3, x(2)=4; при t =3 y(3)=6, x(3)=9 (рис.2.).

рис. 1 рис. 2

Вычисление пределов последовательностей и функций.

Для вычисления пределов последовательностей и функций обычно используют замечательные пределы и правило Лопиталя. Часто прямое использование указанных методов не всегда возможно и требуется предварительно произвести алгебраические или тригонометрические преобразования тех выражений, от которых следует искать предел. Приведем сначала некоторые основные определения из теории пределов.

Определение 1. Пределом функции f(x) при x→∞ называется число b, если для любого ε (где ε – сколь угодно малое положительное число) можно найти такое значение аргумента x=xo, начиная с которого выполняется неравенство |f(x)-b|<ε

Обозначение:  .

Определение 2. Пределом функции f(x) при x→a называется число b, если для любого  сколь угодно малого положительного числа ε существует такое положительное число δ, что для всех значений x, удовлетворяющих неравенству |x-a|<δ, выполняется неравенство |f(x)-b|<ε.

Обозначение: 

Определение 3. Функция α=α(x) называется бесконечно малой при x→xo или при x→∞, если   или  .

Свойства бесконечно малых функций.

1.  Алгебраическая сумма конечного числа бесконечно малых функций есть функция бесконечно малая.

2.  Произведение бесконечно малой величины на ограниченную функцию (постоянную, другую бесконечно малую величину) есть величина бесконечно малая.

3.  Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

Определение 4. Функция A=A(x) называется бесконечно большой при x→xo, если предел этой функции стремится к бесконечности.

Свойства бесконечно больших функций.

1.  Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.

2.  Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.

3.  Частное от деления бесконечно большой величины на функцию, имеющую конечный предел, есть величина бесконечно большая.

Теорема. Связь между бесконечно малой величиной и бесконечно большой величиной. Если функция α(x) бесконечно малая при x→xo (x→∞), то функция f(x)=1/α(x) - является бесконечно большой величиной при x→xo (x→∞). И, обратно, если функция A(x) бесконечно большая при  x→xo (x→∞), то функция  f(x)=1/A(x) - является бесконечно малой величиной при x→xo (x→∞).

Теоремы о пределах.

1.  Если функция имеет конечный предел, то он единственный.

2.  Предел алгебраической суммы нескольких функций равен алгебраической сумме пределов этих функций: lim (f(x)+g(x)) = lim f(x)+lim g(x)

3.  Предел произведения нескольких функций равен произведению пределов этих функций: lim (f(x)∙g(x)) = lim f(x) ∙ lim g(x)

4.  Предел частного равен частному пределов, если предел делителя существует и не равен нулю:

.

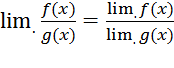5.  Первый замечательный предел:

Эквивалентные бесконечно малые величины при x→0: sin x~x, tg x~x.

Следствия из 1-ого замечательного предела:

 

6.  Второй замечательный предел:

е- основание натурального логарифма.

Следствия из 2-ого замечательного предела:

; ; .

При вычислении пределов используют основные теоремы о пределах, свойства непрерывных функций и правила, вытекающие из этих теорем и свойств.

Правило 1. Чтобы найти предел в точке xo функции, непрерывной в этой точке, надо в функцию, стоящую под знаком предела, вместо аргумента x подставить его предельное значение xo.

Пример: найти предел частного при x→2

Правило 2. Если при отыскании предела дроби предел знаменателя равен нулю, а предел числителя отличен от нуля, то предел такой функции равен +∞ или -∞.

Пример: найти предел частного при x→3

Правило 3. Если при отыскании предела дроби предел знаменателя стремится к бесконечности, а предел числителя отличен от нуля, то предел такой функции равен нулю.

Пример: найти предел отношения при x→π/2

Часто подстановка предельного значения аргумента приводит к неопределенным выражениям вида:

  .

Нахождение предела функции в этих случаях называется раскрытием неопределенности. Для раскрытия неопределенности приходится, прежде чем перейти к пределу, проводить преобразования данного выражения. Для раскрытия неопределенностей используют различные приемы.

Правило 4. Неопределенность вида   раскрывается путем преобразования функции, стоящей под знаком предела для того, чтобы в числителе и знаменателе выделить множитель, предел которого равен нулю, и, сократив на него дробь, найти предел частного. Для этого числитель и знаменатель либо раскладывают на множители, либо умножают на сопряженные числителю и знаменателю выражения.

Пример: найти предел отношения многочленов при x→2

Пример: найти предел при x→4

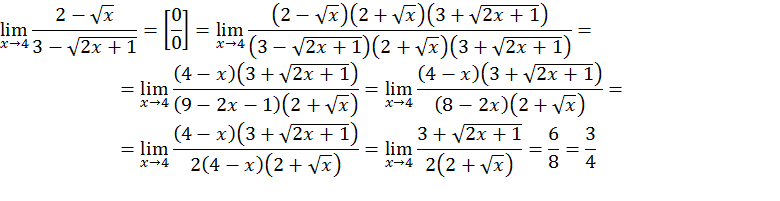
Правило 5. Если выражение, стоящее под знаком предела содержит тригонометрические функции, тогда для раскрытия неопределенности вида   используют первый замечательный предел.

Пример: найти предел отношения двух тригонометрических функций при x→0

Пример: найти предел при x→0. Для решения задачи используем тригонометрические преобразования:

 

При решении следующих задач используется так называемый третий замечательный предел.

Правило 6. Чтобы раскрыть неопределенность вида   при x→∞ дробно-рационального выражения, числитель и знаменатель дроби необходимо разделить на старшую степень аргумента и находить далее предел частного.

Возможны результаты:

1)  искомый предел равен отношению коэффициентов при старших степенях аргумента числителя и знаменателя, если старшие степени числителя и знаменателя дроби одинаковы;

2)  предел дробно-рационального выражения стремится к бесконечности, если старшая степень аргумента числителя больше старшей степени аргумента знаменателя;

3)  предел равен нулю, если старшая степень аргумента числителя меньше старшей степени аргумента знаменателя.

Примеры: найти предел при x→∞

   

т.к. 

Степени равны, значит, предел равен отношению коэффициентов при старших степенях, т.е.  .

Найти предел при x→∞

 

Степень числителя  , знаменателя – 1, значит, предел равен ∞.

Найти предел при x→∞

 

Степень числителя 1, знаменателя –  , значит, предел равен 0.

Правило 7. Чтобы раскрыть неопределенность вида (∞-∞), числитель и знаменатель дроби, находящейся под знаком предела, необходимо умножить на сопряженные выражения.

Пример: найти предел при x→∞

Правило 8. Чтобы раскрыть неопределенность вида   обычно используют второй замечательный предел и его следствия.

Можно доказать, что

Пример: найти предел при x→∞

Пример: найти предел при x→∞

Пример: найти предел при x→0

При решении примеров, в которых встречаются тригонометрические функции и аргумент x→0, используют следствия из первого замечательного предела. Бесконечно малые величины заменяют эквивалентными.

Пример: найти предел при x→0

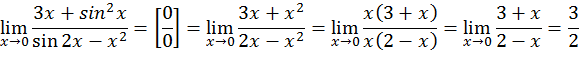
Пример: найти предел при x→2

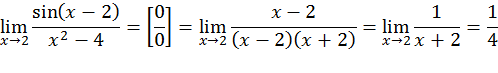
При x→2, разность (x-2)→0, следовательно, можно заменить sin(x-2) эквивалентно малой величиной (x-2).