
elm-04
.pdf
о копараллельную
ïëизВыделимвобъ¼мцилиндрапластинкеараллельнымиоднородноготинкув видеобразующимиэлементарныйтонкогодиэлектрикаполю .
~n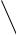
~
внутрипластинки основаниямиE
ï .
~ |
S |
~ |
E |
|
|
|
|
P |
|
α |
~n |
|
ℓ |
|
α |
+Δq |
|
~ |
|
|
P |
|
|
− q |
|
|
S на поверхности
 êòîð ~
связанныеТеоремадляктрическоговектораP ауссазаряды
~
Условияравенства нулюP
длясмещенияэл вектора ρ′
~
Св зь междуD
~
D è
~
E 14/32
|
|
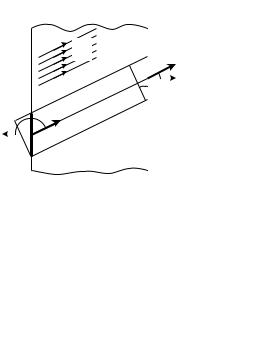
V = ℓ |
S cos α |
|
|
~ |
S |
|
|
|
|
|
|||
моментДипольныйα риваемыйбъ¼ме |
~ |
|
|
|
E |
|
|
|
~ |
|
|
|
|||
~n |
|
|
|
|
|
P |
|
|
|||||||
P |
|
|
|
|
|
|
 êòîð ~ |
|
|
||||||
|
|
|
|
V : |
|
|
|
|
|
|
α |
|
дляТеоремасвязанныектрическоговектораP ауссазаряды |
||
|
|
|
|
|
|
|
|
|
|
~n |
|
|
|||
|
|
|
|
|
|
|
α |
ℓ |
|
|
|
равенстваУсловия |
íóëþP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
pãäå= P |
V = P ℓ S cos α, |
|
~ |
+Δq |
|
|
|
~ |
|
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
смещенияэл вектора |
ρ′ |
||
|
|
|
|
|
|
|
|
P |
|
|
|
|
äëÿ |
|
|
|
|
считать.линдрдиполемповерхностнаядипольным моментом |
|
|
|
|
|
||||||||
|
такжемодульполяризации |
|
~n |
|
|
|
|
|
|
|
|||||
можновектораассмаP |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
− q |
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Св зь междуD |
|
|
Приравнявсвязанных зарядовдипольные′ |
моменты,′ |
получим:плотность |
|
|
~ |
|
|||||||||
|
|
D è |
|||||||||||||
p = |
qℓ = σ |
Sℓ, ãäå σ |
|
|
|
|
|
~ |
15/32 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
ãäå |
P ℓ |
|
′ |
ℓ |
|
′ |
= P cos α = Pn |
S cos α = σ |
S |
σ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn проекция P íà внешнюю нормаль.
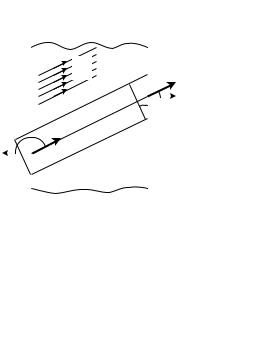
αЗначит |
|
Pn > 0 |
|
~ |
S |
|
|
|
||
′ |
|
|
|
|
E |
|
|
|
~ |
|
Слевазарядповерхнσ >óãîë0,ложистный.поверх.связанныйельный. |
|
|
|
|
|
P |
|
|||
|
|
|
|
|
|
ℓ |
|
α |
~n |
|
|
α тупой. |
|
α |
|
|
|
|
|||
|
|
+Δq |
|
|
|
|||||
|
|
|
|
|
||||||
|
|
~ |
|
|
|
|||||
|
|
′ |
|
|
P |
|
|
|
|
|
Вспомним,связанныйотрицательчто íостный. , . е. |
~n |
|
|
|
|
|
|
|||
Pn |
< 0 |
σ < 0 |
|
|
|
|
|
|
||
|
~ |
|
~ |
|
− q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
P = κε0E. Значит |
|
|
|
|
|
||||
ãäå |
|
|
σ′ = κε0En, |
|
|
|
|
|
||
En |
|
|
|
|
|
|
|
|
|
|
поля внутринормальнаядиэлектрикасоставляющая. напряж¼нности |
|
|
||||||||
 êòîð ~
связанныеТеоремадляктрическоговектораP ауссазаряды
~
Условияравенства нулюP
длясмещенияэл вектора ρ′
~
Св зь междуD
~
D è
~
E 16/32

 êòîð ~
связанныеТедля вектораемаP ауссаиз ряды
~
УсловияравенстваИнтегральнаяДиîðìàеренциальнаíóëþP
3. Теорема аусса для вектора ~
P
дляТеоремасмещенияэлВ кторктрическоговекторааусса ρ′
~
Св зь междуD
~
D è
~
E 17/32

Пустьзамкнут поверх ость
Найд¼мзарядыполэлектричПриохва ризувключенииывпроизвольнаясмещаютсязаряд,скогочастьвышедшийïîëвнешнегодиэлектрикаожительныеяотносительночерез. элементотрицательнS dS ûõ. ~
E
поверхности. |
dS замкнутой |
 êòîð ~
связанныеТедля вектораемаP ауссаиз ряды
~
УсловияравенстваИнтегральнаяДиîðìàеренциальнаíóëþP
дляТеоремасмещенияэлВ кторктрическоговекторааусса ρ′
~
Св зь междуD
~
D è
~
E 18/32
|
|
|
|
~ |
 êòîð ~ |
|
|
|
|
|
|
P |
|
|
|
|
|
|
~n |
|
|
|
|
|
|
dS |
α |
ℓ+ |
|
|
|
|
|
S |
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
дляТесвязанныевектораемаP ауссаиз ряды |
||
|
|
ℓ− |
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равенстваУсловияДиИнтегральнаяîðìàеренциальнаíóëþP |
||
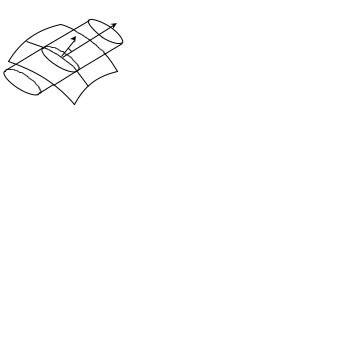
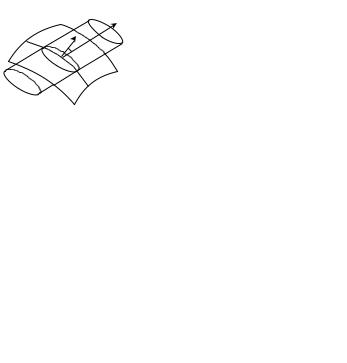
• Через dS наружу выйдет положительныйзаряд |
|
|
|||||
′ ицательноговойд¼т внутрь отрицательный |
|
|
|
||||
ρ+ |
V+ |
|
|
|
|
|
|
′ |
äðîâ,ãäå |
|
|
îáú¼ìû |
|
|
|
öèë |
V± = ℓ±dS cos α |
косых |
|
|
|||
ρ− |
V− |
|
|
|
|||
|
|
|
|
|
смещенияэлВ кторктрическоговекторааусса ′ |
||
|
|
|
|
|
Теорема |
|
|
|
|
|
|
|
äëÿ |
|
ρ |
|
|
ℓ± зарядовсмещения. положительного и |
|
||||
îò |
|
|
|
||||
|
носуотрицательногопротивоположномзаряда,следовательно,заряданаправленииэквивалентенчерез |
|
|
||||
• ïîПереносложителверхность |
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
Св зь междуD |
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
~ |
D è |
|
|
|
|
|
|
19/32 |
|
|
|
|
|
|
|
E |
|
|
dS наружу выходит заряд
dq′ = ρ′+ℓ+dS cos α + |ρ′−ℓ−dS cos α|
|
|
|
|
~ |
 êòîð ~ |
|
|
|
|
|
|
P |
|
|
|
|
|
|
~n |
|
|
|
|
|
|
dS |
α |
ℓ+ |
|
|
|
|
|
S |
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
дляТесвязанныевектораемаP ауссаиз ряды |
||
|
|
ℓ− |
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равенстваУсловияДиИнтегральнаяîðìàеренциальнаíóëþP |
||
• Через dS наружу выйдет положительныйзаряд |
|
|
|||||
′ ицательноговойд¼т внутрь отрицательный |
|
|
|
||||
ρ+ |
V+ |
|
|
|
|
|
|
′ |
äðîâ,ãäå |
|
|
îáú¼ìû |
|
|
|
öèë |
V± = ℓ±dS cos α |
косых |
|
|
|||
ρ− |
V− |
|
|
|
|||
|
|
|
|
|
смещенияэлВ кторктрическоговекторааусса ′ |
||
|
|
|
|
|
Теорема |
|
|
|
|
|
|
|
äëÿ |
|
ρ |
|
|
ℓ± зарядовсмещения. положительного и |
|
||||
îò |
|
|
|
||||
|
носуотрицательногопротивоположномзаряда,следовательно,заряданаправленииэквивалентенчерез |
|
|
||||
• ïîПереносложителверхность |
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
Св зь междуD |
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
~ |
D è |
|
|
|
|
|
|
19/32 |
|
|
|
|
|
|
|
E |
|
|
dS наружу выходит заряд
dq′ = ρ′+ℓ+dS cos α + |ρ′−ℓ−dS cos α|

• |
ãäå |
|
|
|
ρ+′ = |ρ−′ | |
|
dq′ = ρ+′ |
(ℓ+ + ℓ−)dS cos α = ρ+′ ℓdS cos α, |
|||
|
|
ℓ = ℓ+ + ℓ−. |
|
|
|
• |
′ |
′ |
′ |
|
|
поляризациимолекулярногоρ+ = nq+, гдемолекуqäèïî+ положительныйя,ы,возникшего вз результатеряд |
|||||
|
(не путать с вектором нормалиn концентрация молекул |
||||
|
|
|
|
|
~n!). Тогда: |
|
dq′ = nq+′ ℓdS cos α = p n dS cos α = P dS cos α, |
||||
|
ãäå |
|
dq |
′ |
~ ~ |
|
|
|
= P dS |
||
|
|
дипольный момент молекулы, ~ |
|||
|
поляризации,p |
~ |
|
P вектор |
|
|
длиной |
|
|
||
|
dS вектор направленный по ~n ñ |
||||
dS.
 êòîð ~
связанныеТедля вектораемаP ауссаиз ряды
~
УсловияравенстваИнтегральнаяДиîðìàеренциальнаíóëþP
дляТеоремасмещенияэлВ кторктрическоговекторааусса ρ′
~
Св зь междуD
~
D è
~
E 20/32

• |
ãäå |
|
|
|
ρ+′ = |ρ−′ | |
|
dq′ = ρ+′ |
(ℓ+ + ℓ−)dS cos α = ρ+′ ℓdS cos α, |
|||
|
|
ℓ = ℓ+ + ℓ−. |
|
|
|
• |
′ |
′ |
′ |
|
|
поляризациимолекулярногоρ+ = nq+, гдемолекуqäèïî+ положительныйя,ы,возникшего вз результатеряд |
|||||
|
(не путать с вектором нормалиn концентрация молекул |
||||
|
|
|
|
|
~n!). Тогда: |
|
dq′ = nq+′ ℓdS cos α = p n dS cos α = P dS cos α, |
||||
|
ãäå |
|
dq |
′ |
~ ~ |
|
|
|
= P dS |
||
|
|
дипольный момент молекулы, ~ |
|||
|
поляризации,p |
~ |
|
P вектор |
|
|
длиной |
|
|
||
|
dS вектор направленный по ~n ñ |
||||
dS.
 êòîð ~
связанныеТедля вектораемаP ауссаиз ряды
~
УсловияравенстваИнтегральнаяДиîðìàеренциальнаíóëþP
дляТеоремасмещенияэлВ кторктрическоговекторааусса ρ′
~
Св зь междуD
~
D è
~
E 20/32

• |
ãäå |
|
|
|
ρ+′ = |ρ−′ | |
|
dq′ = ρ+′ |
(ℓ+ + ℓ−)dS cos α = ρ+′ ℓdS cos α, |
|||
|
|
ℓ = ℓ+ + ℓ−. |
|
|
|
• |
′ |
′ |
′ |
|
|
поляризациимолекулярногоρ+ = nq+, гдемолекуqäèïî+ положительныйя,ы,возникшего вз результатеряд |
|||||
|
(не путать с вектором нормалиn концентрация молекул |
||||
|
|
|
|
|
~n!). Тогда: |
|
dq′ = nq+′ ℓdS cos α = p n dS cos α = P dS cos α, |
||||
|
ãäå |
|
dq |
′ |
~ ~ |
|
|
|
= P dS |
||
|
|
дипольный момент молекулы, ~ |
|||
|
поляризации,p |
~ |
|
P вектор |
|
|
длиной |
|
|
||
|
dS вектор направленный по ~n ñ |
||||
dS.
 êòîð ~
связанныеТедля вектораемаP ауссаиз ряды
~
УсловияравенстваИнтегральнаяДиîðìàеренциальнаíóëþP
дляТеоремасмещенияэлВ кторктрическоговекторааусса ρ′
~
Св зь междуD
~
D è
~
E 20/32
