
- •Введение
- •1. ОсновНые понятия и определения теории автоматического управления
- •1.1. Краткие сведения по истории развития систем автоматического управления
- •1.2. Обобщенная структурная схема сау
- •1.2. Классификация сaу
- •2. Математическое описание линейных сау
- •2.1. Составление и линеаризация дифференциальных уравнений сау
- •2.2. Основные свойства преобразования Лапласа. Операторные уравнения сау. Передаточные функции линейных звеньев и систем
- •Основные свойства (теоремы) преобразования Лапласа
- •Изображения по Лапласу типовых сигналов
- •2.3. Временные и частотные характеристики звеньев и систем
- •2.4. Элементарные звенья систем автоматического управления
- •Пропорциональное (усилительное, безинерционное, масштабирующее) звено
- •Интегрирующее звено
- •Идеальное дифференцирующее звено
- •Апериодическое звено первого порядка
- •Реальное дифференцирующее звено
- •Инерционное звено второго порядка
- •Звено чистого запаздывания
- •Интегро-дифференцирующее звено
- •Пропорционально-интегральный регулятор (пи-регулятор)
- •2.5. Неминимально-фазовые звенья
- •2.6. Эквивалентные преобразования структурных схем линейных сау
- •2.7. Передаточные функции многоконтурных систем
- •Вопросы для самопроверки
- •3. Анализ устойчивости линейныхсау
- •3.1.Понятие устойчивости линейных систем
- •3.2.Алгебраический критерий устойчивости Гурвица
- •3.3.Частотные критерии устойчивости Михайлова и Найквиста
- •3.4.Запасы устойчивости
- •3.5.Оценка устойчивости по логарифмическим амплитудно- и фазо-частотным характеристикам
- •3.6.Устойчивость систем с запаздыванием
- •Вопросы для самопроверки
- •4. Качество динамических характеристик сау
- •4.1. Показатели качества процесса регулирования
- •4.2. Частотные критерии качества
- •4.3. Корневые критерии качества
- •4.4. Интегральные критерии качества
- •Вопросы для самопроверки
- •5. Оценка точности сАу
- •5.1. Стационарные режимы сау. Передаточные функции статических и астатических систем
- •5.2. Коэффициенты ошибки системы
- •5.3. Системы комбинированного управления
- •Вопросы для самопроверки
- •6. Анализ сау в пространстве состояния
- •6.1. Основные положения метода переменных состояния
- •6.2. Способы построения схем переменных состояния
- •Метод прямого программирования
- •Метод параллельного программирования
- •Метод последовательного программирования
- •6.3. Решение уравнений состояния линейных стационарных сау. Вычисление фундаментальной матрицы
- •Вопросы для самопроверки
- •7. Коррекция линейных сАу
- •7.1. Цели и виды коррекции
- •Последовательные корректирующие звенья
- •Параллельные корректирующие звенья
- •7.2. Частотный метод синтеза корректирующих устройств
- •Построение лах в низкочастотном диапазоне
- •Построение лах в среднечастотном диапазоне
- •Зависимость колебательности от значений hи h1
- •Построение лах в высокочастотном диапазоне
- •7.3. Последовательные корректирующие устройства
- •7.4. Параллельные корректирующие устройства
- •7.5. Техническая реализация корректирующих звеньев
- •Пассивные четырехполюсники постоянного тока
- •Пассивные корректирующие четырехполюсники
- •Активные корректирующие звенья
- •Активные четырехполюсники постоянного тока
- •Вопросы для самопроверки
- •8. Нелинейные системы автоматического управления
- •8.1. Особенности нелинейных систем и методы их анализа
- •8.2. Исследование нелинейных систем на фазовой плоскости
- •8.3. Метод гармонической линеаризации нелинейных звеньев
- •Коэффициенты гармонической линеаризации типовых нелинейностей
- •8.5. Методы определения параметров автоколебаний
- •Вопросы для самопроверки
- •Курсовая работа
- •Задание для расчета линейной caу
- •Варианты задания для расчета линейной сау
- •Варианты передаточных функций линейной сау
- •Задание для расчета нелинейной сау
- •Варианты задания для расчета нелинейной сау
- •Варианты структурных схем нелинейных систем Варианты статических характеристик нелинейного элемента
- •Экзаменационные вопросы
- •Литература
2.4. Элементарные звенья систем автоматического управления
Математическое описание системы начинают с разбиения ее на звенья и составления математических моделей этих звеньев. При этом передаточная функция, временные и частотные характеристики, которыми описываются звено, не учитывают его физической природы, т.е. рассматривается математическая модель, а не реальное конструктивное исполнение и принципы работы звена. Очевидно, что при составлении математического описания системы целесообразно ориентироваться на математические модели звеньев стандартного вида, так называемые типовые звенья. Рассмотрим их основные характеристики.
Пропорциональное (усилительное, безинерционное, масштабирующее) звено
Пропорциональное (усилительное, безинерционное, масштабирующее) звено – это звено, выходной сигнал которого пропорционален входному сигналу:
![]() ,
,
где k – коэффициент усиления звена.
Операторное уравнение звена:
![]()
а его передаточная функция:
W(p) = k.
Амплитудно-фазовая характеристика: W(jω)= k.
Соответственно вещественная и мнимая частотные характеристики:
Р(ω) = k, Q(ω) = 0.
Амплитудно- и фазо-частотная характеристики звена:
A(ω)
=![]() ,
,
![]() .
.
Переходная функция звена (рис. 2.7а):
![]() .
.
Логарифмическая АЧХ звена в соответствии с выражениями (2.41):
![]() .
.
Графики логарифмической амплитудно- и фазо-частотной характеристик приведены на рис.2.7б.
Примерами технической реализации пропорциональных звеньев являются потенциометр, полупроводниковый усилитель, зубчатая передача и т.п.
Рис.
2.7а
a)
Переходная функция пропорционального
звена
б)
Логарифмические амплитудно- и
фазо-частотная характеристики
пропорционального
звена
Рис.
2.7б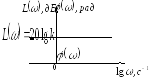

Интегрирующее звено
Интегрирующее звено – это звено, выходной сигнал которого пропорционален интегралу по времени от входного сигнала:
![]()
Операторное
уравнение, связывающее изображения
входного и выходного сигналов звена:
![]() ,
а его передаточная функция:
,
а его передаточная функция:
![]() .
.
Амплитудно-фазовая характеристика звена (рис. 2.8):
W(jω)=
![]() .
.
Вещественная и мнимая и частотные характеристики:
![]()
 .
.
Амплитудно- и фазо-частотная характеристики:
A(ω)
![]() .
(2.42)
.
(2.42)
Логарифмическая АЧХ звена с учетом (2.41) и (2.42) описывается выражением:
![]() .
.
Этому
уравнению соответствует прямая линия
с наклоном
-20 дБ/дек.
Логарифмическая ФЧХ
не зависит
от частоты и равна
![]() .
Графики логарифмической амплитудно- и
фазочастотной
.
Графики логарифмической амплитудно- и
фазочастотной
характеристик приведены на рис. 2.8а.
Выражения для переходной функции и функции веса интегрирующего звена (рис. 2.9б):
![]() w
(t)
w
(t)![]() .
.
Примеры технической реализации интегрирующего звена: усилитель постоянного тока с большим коэффициентом усиления, в цепь обратной связи которого включен конденсатор.
Идеальное дифференцирующее звено
Идеальное дифференцирующее звено – это звено, выходной сигнал которого пропорционален производной по времени от входного сигнала:
![]() .
.
Операторное уравнение, связывающее изображения входного и выходного сигналов звена:
![]() ,
,
а передаточная функция звена:
![]() .
.
П ередаточная
функция такого звена не удовлетворяет
условиям физической реализуемости,
поэтому звено называется идеальным.
ередаточная
функция такого звена не удовлетворяет
условиям физической реализуемости,
поэтому звено называется идеальным.

а)
Логарифмические амплитудно и
фазо-частотная характеристики интегрирующего
звена б)
Переходная функция и функция веса
интегрирующего звена интегрирующего
звена
Амплитудно-фазовая характеристика звена (рис. 2.10):
![]() .
.
Амплитудно-
и фазо-частотные характеристики звена:
A(ω)
= kω,
![]() .
.
Переходная функция звена:
![]() где
где
![]() – дельта-функция.
– дельта-функция.
Логарифмическая АЧХ звена описывается выражением:
![]() .
.
Г рафики
логарифмических амплитудно- и
фазо-частотной характеристик приведены
на рис. 2.11.
рафики
логарифмических амплитудно- и
фазо-частотной характеристик приведены
на рис. 2.11.
