Основные свойства (теоремы) преобразования Лапласа

1. Линейность преобразования. Для любых постоянных и

. (2.8)

2. Дифференцирование оригинала. Если производная является функцией-оригиналом, т.е. обладает указанными тремя свойствами, то, где=,. И вообще, еслиn-я производная 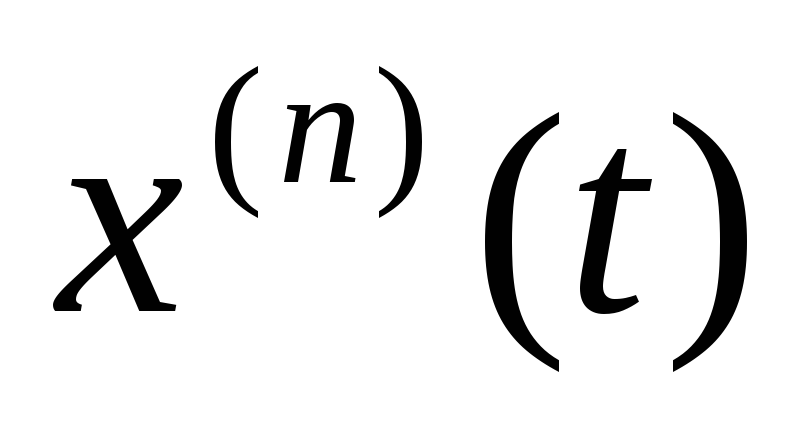является функцией-оригиналом, то

,

где ,k=0,1,…n-1.

Если начальные условия нулевые, т.е. , то последняя формула принимает вид:

. (2.9)

Таким образом, при нулевых начальных условиях дифференцированию соответствует умножение изображения на р.

3. Интегрирование интеграла. Интегрирование оригинала сводится к делению изображения на р:

. (2.10)

4. Теорема запаздывания. Для любого положительного числа

. (2.11)

5. Теорема умножения изображения. Если и– оригиналы,и– их изображения, то

. (2.12)

Интеграл правой части равенства называют сверткой функций ии обозначают:

=.

6. Теоремы о предельных значениях. Если – оригинал, а– его изображение, то

, (2.13)

и при существовании предела

. (2.14)

7. Теорема разложения. Если изображение сигнала представляет собой дробно-рациональное выражение, т.е.

,

причем степень полинома числителя меньше степени полинома знаменателя и все n корней уравнения простые, то для нахождения оригинала, соответствующего изображению, может быть использована формула (формула разложения):

(2.15)

где - корень уравнения,.

В таблице 2.1 приведены выражения изображения Лапласа для некоторых типовых сигналов.

Таблица 2.1

Изображения по Ла­пласу типовых сигналов

Оригинал	Изображение	Оригинал	Изображение
δ(t)	1
1(t)		sin()
		cos()

Применяя преобразование Лапласа к дифференциальному уравнению (2.5) и считая начальные условия нулевыми, получим следующее операторное уравнение, связывающее изображения входного и выходногосигналов системы:

..+++..+(2.16)

или

,

где А(p) =;В(р)=.

Введем в рассмотрение передаточную функ­цию звена (или системы) равную отношению изображения по Ла­пласу выходного сигнала к изображению по Лапласу входного сигнала при нулевых начальных условиях:

.(2.17)

Из выражений (2.16) – (2.17) следует, что и

. (2.18)

Выражение (рис. 2.18) связывает изображение выходного сиг­нала системы с изображением входного сигнала. Передаточная функция W(p) характеризует динамические свойства САУ, она не зависит от входного сигнала и полностью определяется коэффициентами и, а те, в свою очередь, – параметрами и структурой системы.

Передаточная функция является дроб­но рациональной функцией относительно оператора пре­образования Лапласа:

. (2.19)

Степень полинома знаменателя передаточной функции определяетпорядок системы. В реальных системах степень полинома числителя передаточной функции не пре­вышает степени полинома зна­менателя: . Это условие называ­ютфизической реализуемостью САУ; оно означает, что нельзя создать систему, пе­редаточная функция которой не удовлетворяла бы этому условию.

Корни полинома числителя передаточной функции (2.19) назы­вают нулями, а корни полино­ма знаменателя – полюсами САУ. При анализе САУ нули и полюсы (особенности передаточной функ­ции) удобно изображать точками на плоскости комплекс­ного переменного (рис. 2.2). Так как коэффициенты передаточной функции – действительные числа, то нули и полюсы могут быть только вещественными () либо комплексно-сопряженными (и) величинами. Если передаточная функ­ция звена или системы не содержит особенностей в правой части плоскости, то систему называют минимально-фазовой, в противном случае ее считают неминимально-фазовой.

Рассмотрим вопросы практического использования материала, изложенного в предыдущих параграфах, применительно к несложному объекту, взятому из электротехники --цепочке(рис. 2.3). Входным сигналом такого объекта является приложенное к цепи напряжение , а выходным сигналом – ток в цепи.Несмотря на предельную простоту рассматриваемого объекта, на его примере можно проиллюстрировать некоторые вопросу, связанные с классификацией САУ. Очевидно, что это непрерывная система, построенная по принципу разомкнутого управления. Кроме того, полагая, что значения активного сопротивления и емкости неизменны, этот объект управления можно отнести к линейным и стационарным. Если приложенное напряжение незменно (), то, с точки зрения теории управления, рассматриваемая электрическая цепь – это система стабилизации, а если напряжение изменяется по определенному закону, например, синусоидальному, то это система программного управления.

Согласно второму уравнению Кирхгофа, дифференциалье уравнение, описывающие рассматриваемую - цепочку, имеет следующий вид:

На основании (2.8) и (2.9) в результате выполнения преобразование Лапласа над обеими частями этого уравнения получим следующее операторное уравнение, связывающее изображения входного и выходного сигналов объекта:

.

Используя определение передаточной функции (2.17), получаем:

,

где – коэффициент усиления, а– постоянная времени объекта, с. Полученная передаточная функция соответствует одному из так называемых типовых звеньев – апериодическому звену первого порядка. Нулей такая передаточная функция не имеет, а для расчета ее полюсов необходимо, записать характеристическое уравнение системы, приравняв к нулю полином знаменателя:

.

Это алгебраическое уравнение первого порядка имеет единственный действительный корень – полюс передаточной функции:

.