4.3. Корневые критерии качества

Эта группа критериев позволяет оценить качество переходных процессов по расположении полюсов и нулей передаточной функции устойчивой замкнутой системы. При исследовании устойчивости САУ оценивалось только расположение полюсов на комплексной плоскости. Оценивая качество переходного процесса, необходимо учитывать и расположение нулей.

К числу корневых критериев качества относят степень устойчивости и степень колебательности.

Степень устойчивости (η) – это расстояние от мнимой оси до ближайшего к ней левого полюса (рис. 4.3, а) или ближайшей пары комплексно сопряженных полюсов замкнутой системы (рис. 4.3, б). В первом случае соответствующая этому полюсу слагаемое в общем решении дифференциального уравнения (3.5) равно:

.

Во втором случае, когда ближайшей к мнимой оси окажется пара комплексно-сопряженных полюсов, им в выражении (3.5) будет соответствовать слагаемое вида:

.

В обоих случаях указанное слагаемое будет затухать медленнее остальных, тем самым определяя в первом приближении длительность переходного процесса:

_.

Степень колебательности определяется только для замкнутых систем, передаточные функции имеют комплексно-сопряженные полюса:

p_i,i+1 = α_i + jβ_i .

Переходная функция таких систем в большей или меньшей степени колебательна. Степень колебательности переходного процесса равна:

,

где φ – наибольший по величине угол, образованный отрицательной вещественной полуосью и лучом, проведенным из начала координат к комплексному полюсу p_i (рис. 4.3, а, б). Среди всех комплексно-сопряженных полюсов системы указанному полюсу соответствует максимальное отношение мнимой части к действительной. Чем больше степень колебательности μ, тем слабее будет затухание колебаний в переходном процессе.

Задавшись предельно допустимыми значениями степени устойчивости η_з и степени колебательности φ_з, можно построить на комплексной плоскости область (рис. 4.3, в), в которой должны находиться полюса системы, показатели качества регулирования которой будут удовлетворять заданным значениям, т.е. η > η_з и μ < μ_з.

4.4. Интегральные критерии качества

Интегральными критериями (оценками) качестваназываются такие, которые одним числом (интегрально) оценивают качество переходного процесса в системе. Кроме того, такие оценки обычно являются интегральными функционалами и выражаются в следующем виде:

где F– заданная функция, определяющая тип интегрального критерия;x(t) – отклонение переходной функции системы от значенияh(∞), которое установится после окончания переходного процесса, т.е.

x(t) = h(∞) – h(t). (4.2)

Как известно, качество переходного процесса в САУ оценивается совокупностью показателей. Зачастую при изменении параметров системы с целью обеспечения требуемых характеристик переходного процесса одни из показателей улучшаются, в то время как другие ухудшаются. В такой ситуации, когда задача выбора оптимальных значений параметров системы оказывается многокритериальной, а потому трудноразрешимой, использование интегральных критериев, оценивающих качество регулирования одним числом, оказывается предпочтительным.

Для монотонного процесса (рис. 4.4, а) интегральной оценкой может служить функционал следующего вида:

называемый линейной интегральной оценкой качества J₁. Ее численное значение равно площади под кривой переходного процесса. Очевидно, что динамика системы тем лучше, чем меньше значение J₁.

Для обеспечения требуемых динамических свойств САУ необходимо выразить величину J₁ через коэффициенты передаточной функции системы, а затем найти оптимальные значения варьируемых параметров, соответствующих минимуму J₁.

Поскольку

,

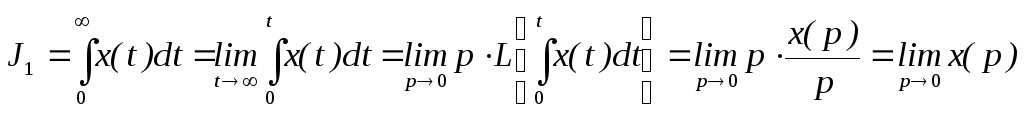и учитывая, что

= ,

(где - передаточная функция замкнутой системы), получаем выражение для расчета величины линейной интегральной оценкой качестваJ₁ по передаточной функции системы:

. (4.3)

Так, например, для системы с передаточной функцией

интегральная оценка J₁ , согласно выражению (4.3), равна:

.

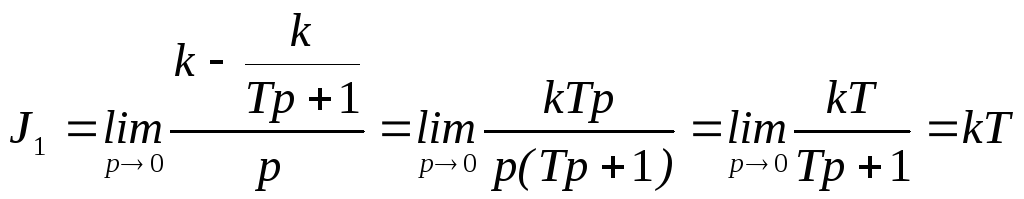Для системы с передаточной функцией

интегральная оценка

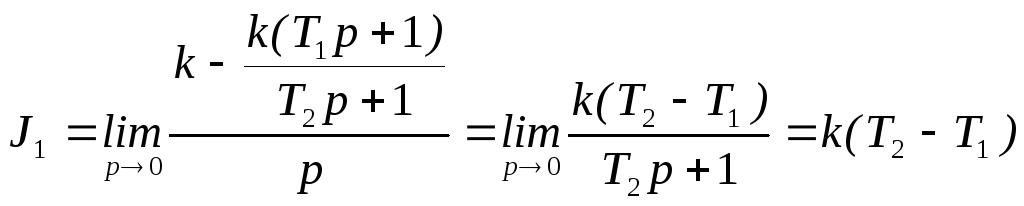
зависит от соотношения постоянных времени и.

Использование линейной интегральной оценки J₁возможно только для монотонных процессов и неприемлемо для оценки качества колебательных систем. Для колебательных процессов величина критерия, равная разности между суммой положительных и отрицательных площадей (см. рис. 4.4, б), не будет однозначно связана с действительным качеством регулирования системы.

Например, ухудшение качества переходного процесса при переходе к незатухающим колебаниям будет сопровождаться уменьшение критерия J₁ до нуля. В связи с этим при наличии перерегулирования в переходном процессе и колебательном его характере применяют квадратичную интегральную оценку качества J₂ следующего вида:

.

Величина квадратичной интегральной оценки J₂ равна площади, ограниченной кривой x²(t) (рис. 4.5, а).

В справочной литературе приведены формулы, выражающие величину критерия J₂ непосредственно через коэффициенты дифференциального уравнения замкнутой системы.

Д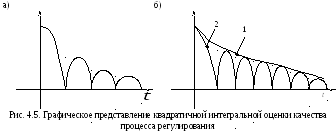анный критерий является наиболее широко используемым интегральным критерием качества, однако в ряде случаев он также не дает достоверной оценки характера переходного процесса. На рис. 4.5, б приведены графикиx²(t) для монотонного процесса (кривая 1) и колебательного процесса (кривая 2). Очевидно, что значение критерия J₂ для колебательного процесса будет меньше, в то время как более предпочтительным является монотонный процесс: ему соответствует плавное изменение выходного сигналы и отсутствие значительных динамических воздействий в системе.

Недостатки рассмотренных интегральных оценок качества обусловили использование обобщенного (улучшенного) интегрального критерия, имеющего в простейшем случае следующий вид:

.

Использование интегральной оценки J₃ позволяет обеспечить в системе быстро затухающий, но достаточно плавный процесс, поскольку наличие в подынтегральном выражении слагаемого ограничивает скорость изменения регулируемой величины, снижая колебательность системы. Чем больше коэффициент , тем значительнее влияние указанного слагаемого, тем более плавным будет переходный процесс, но зато и более длительным.

В качестве интегральных критериев используются и функционалы более общего вида. Иногда в выражении интегральной оценки вводится время t в явном виде.

Наиболее широко интегральные критерии применяются в теории оптимальных систем автоматического управления.