2.6. Эквивалентные преобразования структурных схем линейных сау

В САУ встречаются три вида соединений звеньев: последовательное, параллельное и соединение звеньев по схеме с обратной связью.

В системе, состоящей из n последовательно соединенных звеньев (рис. 2.28) выходной сигнал предыдущего звена равен входному сигналу последующего.

И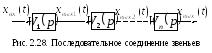зображения по Лапласу выходных сигналов этих звеньев равны:

x_вых1(p) = W₁(p)x_вх(p); x_вых2(p) = W₂(p) x_вых1(p); … x_вых(p) = W_n(p)x_вых(n)(p).

Откуда

x_выхx_вх(p).

Следовательно, передаточная функция системы примет вид:

. (2.57)

Таким образом, передаточная функция последова­тельно соединенных звеньев равна произведению пере­даточных функций этих звеньев.

Частотные характеристики последовательно соеди­ненных звеньев:

где A(ω) = A₁(ω)A₂(ω)…A_n(ω); .

Логарифмическая амплитудно-частотная характеристика звеньев, соединенных последовательно:

.(2.58)

Следовательно, логарифмические амплитудно- и фазо-частотная характеристики системы, состоящей из последовательно сое­диненных звеньев, равны сумме ЛАХ и ФЧХ отдельных звеньев. Это существенно упрощает построение логарифмических частотных характеристик, по сравнению с обычными характеристиками.

Передаточная функция минимально-фазовой системы в общем случае может быть записана в виде:

. (2.59)

В выражении (2.59) сомножители в числителе определяют нули передаточной функции, а именно:

• сомножитель 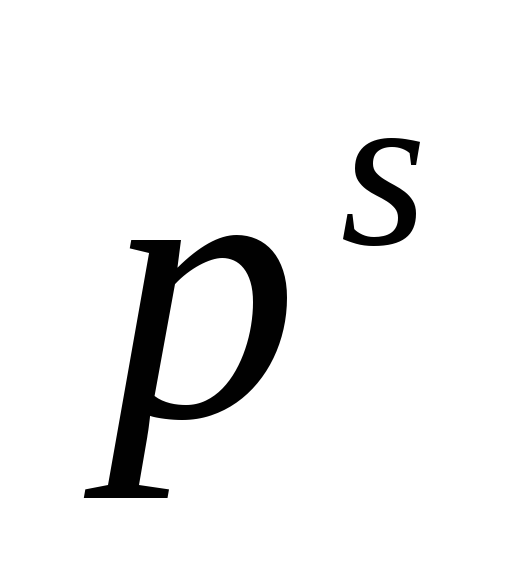соответствует нулевому нолю кратности,

• сомножитель 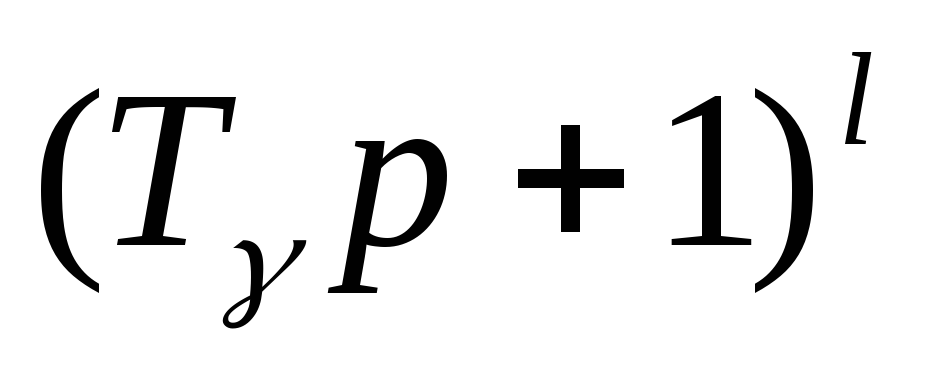– действительному нолю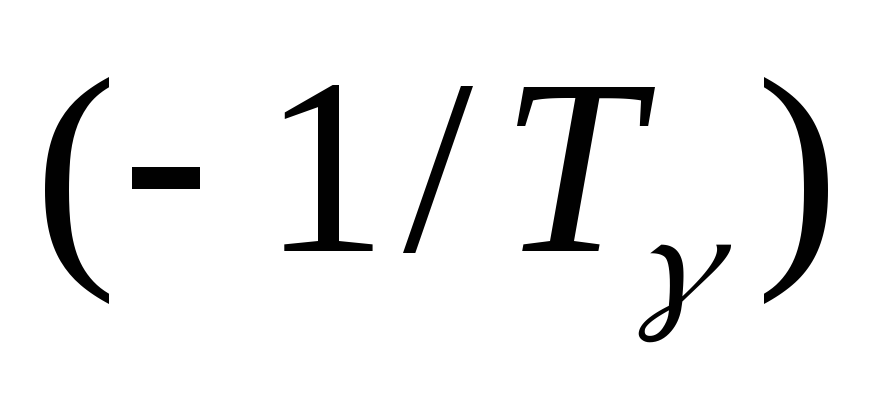кратностиl,

• сомножитель 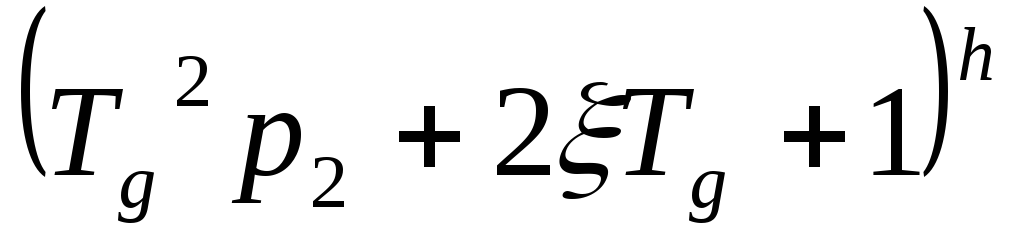– паре комплексно-сопряженных нолей кратности .

Аналогичные сомножители в знаменателе выражения (2.59) определяют полюса передаточной функции, а именно:

• сомножитель 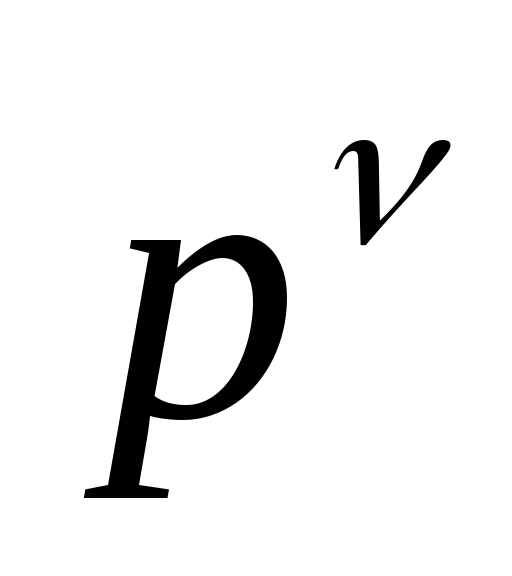соответствует нулевому полюсу кратности,

• сомножитель 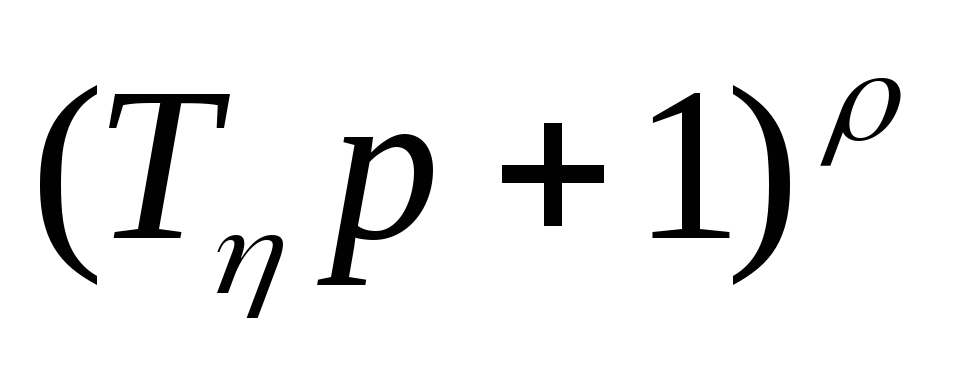– действительному полюсу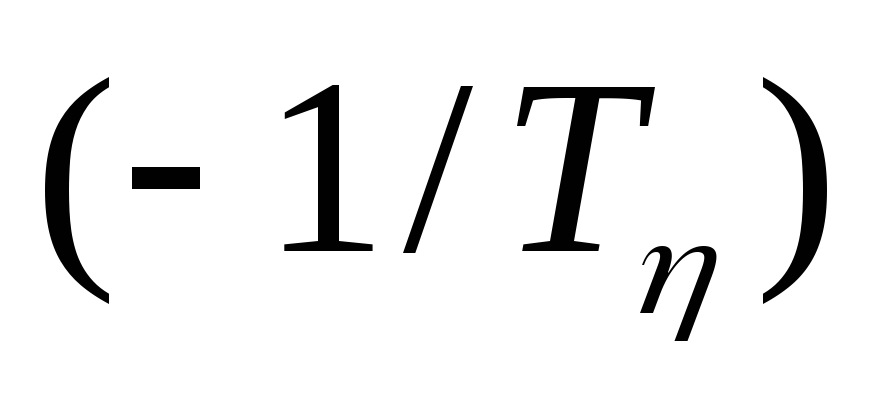кратности,

• сомножитель 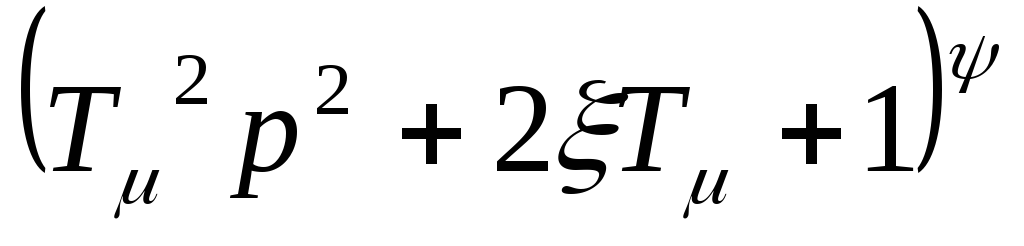– паре комплексно-сопряженных полюсов кратности .

Очевидно, что в зависимости от соотношения s и передаточная функция (2.59) может иметь только один тип особенностей: либо нулевые ноли, либо нулевые полюса. Кроме того, предполагается, что в (2.59) для коэффициентов демпфирования выполняются неравенства: 0 <ζ < 1.

Формально передаточная функция (2.59) представляет собой произведение нескольких сомножителей, что соответствует последовательному соединению звеньев, и для вычисления можно воспользоваться выражением (2.58). При этом построение ЛАХ системы осуществляется без предварительного построения ЛАХ отдельных звеньев по следующим правилам.

На оси частот в порядке возрастания указываются все частоты сопряжения ЛАХ, определяемые соответствующими постоянными времени:= 1/.

Построение ЛАХ начинается на частотах, меньших самой малой частоты сопряжения .

Если при этом в выражении (2.59) выполняется равенство s = = 0 (система не имеет нулевых полюсов и нолей), то первая низкочастотная асимптота ЛАХ проводится параллельно оси частот на уровне 20lgk до частоты

Если в выражении (2.59) s , а= 0, то уравнение низкочастотной асимптоты:

, (2.60)

т.е. ЛАХ до наименьшей частоты сопряжения проводится с наклоном (+20∙s) дБ/дек.

Если в выражении (2.48) s =, а, то уравнение низкочастотной асимптоты:

, (2.61)

и наклон ЛАХ до наименьшей частоты сопряжения равен -20∙дБ/дек.

Для построения низкочастотной асимптоты ЛАХ необходимо для произвольной частоты меньшей или равнойпо выражениям (2.60) или (2.61) рассчитать величинуи через точку с координатами (;) провести ЛАХ с необходимым наклоном.

На частоте производится излом ЛАХ с изменением ее наклона, величина которого определяется видом сомножителя в выражении (2.59), которому соответствует сопрягающая частота. Наклон ЛАХ на частотеизменяется по отношению к предыдущему наклону на +20∙l, если соответствует постоянной времениT из сомножителя вида в числителе передаточной функции (2.59).

Если сомножитель вида , соответствующийприсутствует в знаменателе (2.59), то изменение наклона составляет -20∙.

В случае, когда соответствует постоянной времениT из сомножителя вида , происходит изменение предыдущего наклона на +40∙h, если указанный сомножитель присутствует в числителе , и на -40∙, если он присутствует в знаменателе.

Таким же образом характеристика продолжается в сторону увеличения частоты, претерпевая соответствующие изломы на каждой сопрягающей частоте . При необходимости вид построенной ЛАХ уточняется путем введения поправок для колебательных звеньев.

Примеры построения ЛАХ по различным передаточным функциям приведены на рис. 2.29.

В системе, состоящей из n параллельно соединенных звеньев (рис. 2.30), на вход каждому из звеньев подается один и тот же сигнал x_вх(p), а их выходные сигналы суммируются:

.

Так как

;

;

……………………………

,

то

x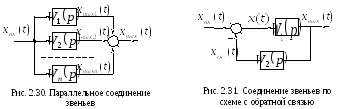_вых(p) = x_вых1(p) +x_вых2(p)+…+x_вых(n)(p) = .

Таким образом, передаточная функция параллельно соединенных звеньев равна сумме передаточных функ­ций отдельных звеньев:

W(p) =. (2.62)

Очевидно, что в случае, когда выходной сигнал какого-либо из параллельно соединенных звеньев поступает в сумматор со знаком «минус», передаточная функция этого звена входит в (2.62) также со знаком «минус».

Рассмотрим структуру системы с обратной связью (рис. 2.31). На вход звена, охваченного обратной связью, подается сигнал рассогласования, равный:

.

Поскольку , то

Изображение выходного сигнала:

x_вых(р)=

откуда

.

Следовательно, передаточная функция замкнутой системы (в замкнутом состоянии) описывается следующим выражением:

Ф(p) = . (2.63)

Передаточная функция (2.63) найдена для случая от­рицательной обратной связи. Если обратная связь поло­жительная, то

Ф(p) = . (2.64)

При анализе и синтезе CАУ, наряду с передаточной функцией (2.63) – (2.64), используются передаточная функция разомкнутой системы и передаточная функция по ошибке.

Передаточная функция разомкнутой системы (замкнутой системы в разомкнутом состоянии):

W(p) = . (2.65)

Передаточная функция по ошибке:

Ф_x(p) =

. (2.66)