Множество – это многое, мыслимое как единое.

Действовать без правил – самое трудное и самое утомительное занятие на этом свете.

А. Мандзони

Глава 2. Операции над множествами

Объединение, пересечение и разность множеств, симметрическая разность множеств, дополнение множества, законы и тождества алгебры множеств, доказательство тождеств с множествами, метод двух включений, метод доказательства от противного, диаграммы Эйлера – Венна

ЦЕЛИ

Освоив эту главу, студенты должны:

• знать основные свойства операций над множествами;

• уметь выполнять операции над множествами;

• уметь доказывать тождества с множествами.

2.1. Объединение множеств

Объединением множеств А и В называют множество С, которое состоит из тех элементов, которые принадлежат или множеству А, или множеству В, или обоим множествам одновременно:

С = А  В,

где  — знак объединения.

Теоретико-множественная запись операции объединения имеет следующий вид:

xC = A  B  xA  xB,

что означает: элемент х принадлежит множеству С, если х принадлежит множеству А или множеству В. Если изобразить элементы множеств А и В точками плоскости, расположенными внутри прямоугольника, то A  B представится множеством точек плоскости, расположенных внутри заштрихованной фигуры (рис.2.1). Такое геометрическое представление множеств называется диаграммой Эйлера-Венна.

Также можно записать: элемент х не принадлежит множеству С, если он не принадлежит множеству A и не принадлежит множеству В:

xC = A  B  xA & xB.

Рис. 2.1. Пример операции объединения множеств А и В

Например, найдем объединение множеств А = { ЭВМ, студент } и В = { 1, 2, стол, ЭВМ, стул }. Результатом будет множество С = А  В = { 1, 2, стол, ЭВМ, стул, студент }.

Приведем основные свойства операции объединения:

• A  A = A - идемпотентность;

• A  B = B  A - коммутативность;

• (A  B)  C = A  (B  C) - ассоциативность;

• A   = A;

• (A  A  B) & (B  A  B).

Объединение в множествах является синонимом сложения в арифметике.

Заметим, что можно объединить не только два, но и любое количество множеств.

Объединением n множеств А₁, А₂, ..., А_n называется множество, обозначаемое: , состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств A_i:

А₁  А₂  А₃  … А_n = .

Мощность объединения множеств равна числу содержащихся в нем неповторяющихся элементов. Например, А = {1, 2, 3}, B = {1, 2, 9, 10}, C = А  В = {1, 2, 3, 9, 10} и мощность |C| = 5.

2.2. Пересечение множеств

Множество С называется пересечением множеств А и В, если оно состоит из тех элементов, которые принадлежат одновременно множеству А и множеству В:

С = А  В,

где  — знак пересечения.

На рис.2.2. приведена диаграмма Эйлера-Венна, иллюстрирующая пересечение множеств А и В. Множество A  B изображено заштрихованной фигурой.

Рис. 2.2. Пример операции пересечения множеств

Теоретико-множественная запись операции пересечения имеет следующий вид:

xC = A  B  xA & xB,

что означает: элемент х принадлежит множеству С, если х одновременно принадлежит множеству А и множеству В.

Соответственно элемент х не принадлежит множеству С, если он не принадлежит множеству А или не принадлежит множеству В:

xC = A  B  xA  xB.

Приведем пример пересечения множеств A = { 1, 2, 3 } и B = { 3, 4, 5, 6 }. Результатом выполнения данной операции будет множество C = A  B = { 3 }.

Свойства операции пересечения:

• A  A = А - идемпотентность;

• A  B = B  A - коммутативность;

• (A  B)  C = A  (B  C) - ассоциативноcть;

• A   = ;

• A  B =А  А  B;

• A  B  А & A  B  B.

Пример, когда пересечение двух множеств равняется пустому множеству, показан с помощью диаграммы Эйлера-Венна на рис. 2.3.

Рис. 2.3. Пример операции пересечения

Отметим, что операция пересечения может выполняться над любым количеством множеств. Пересечением n множеств А₁, А₂, ..., А_n называется множество, обозначаемое через , состоящее из тех и только тех элементов, которые принадлежат каждому из множеств:

_.

_{Примеры пересечения трех и четырех множеств на основе диаграмм Эйлера-Венна показаны на рис. 2.4, 2.5.}

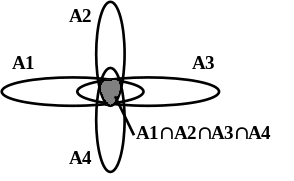
Рис. 2.4. Пример пересечения Рис. 2.5. Пример пересечения

трех множеств четырех множеств

Например, пересечением множеств А = {1, 2, 3}, B = {1, 2, 9, 10} является множество C = {1, 2} и его мощность |C| = 2.