3.4. График

График — это множество каждый элемент которого является парой или кортежем длины 2. Множество Р называется графиком, если каждый элемент его пара.

Например, множество Р = {<a, b>, <a, 1>, <c, d>} является графиком.

Если М — произвольное множество, то М², а также любое множество С  М² является графиком. В частности графиком является множество D² действительных чисел. Пусть заданы множества A и B, тогда А × В, С А × В являются графиками.

Понятие графика является обобщенным. В принципе оно происходит от понятия графика функции.

Областью определения графика Р называется множество пр₁Р (проекция на первую ось (ось абсцисс) данного графика).

Областью значения графика называется множество проекций на вторую ось (ось ординат) (пр₂Р).

Легко видеть, что если Р — график, тогда если Р = , то пр₁Р =   пр₂Р = .

Рассмотрим операции над графиками. Известны две основные операции: инверсия графика и композиция графика.

1) Инверсия.

Инверсия графика определяется через инверсию кортежа.

Инверсией графика Р называют множество инверсий пар из Р.

Например, Р = {<c, d>, <a, b>}, Р^-1 = {<d, c>, <b, a>}.

График Q называется инверсией графика Р, если   Q тогда и только тогда, когда ^-1  Р, где  - произвольный кортеж.

В теоретико-множественном виде запишем:

^-1  Р    Р^-1,

  Р  ^-1  Р^-1

График Р называется симметричным, если он наряду с любой своей парой содержит ее инверсию.

Например, график P = {<a, b>, <b, a>} является симметричным.

Пусть М — произвольное множество. Тогда считают М — множество всех пар вида <x, x>, где x присутствует во всем множестве М.

Таким образом, если М = {a, b}, то М = {<a, a>, <b, b>} — является симметричным графиком и называется диагональю.

2) Композиция.

График R является композицией двух графиков P и Q, а также <x, y>  R, тогда и только тогда, когда z такое, что <x, z>  P & <z, y>  Q.

Переход от графиков P и Q к их композиции (P • Q) называется операцией композиции (или просто композицией) графиков P и Q.

Например, пусть Р = {<a, a>, <a, c>}, а Q = {<a, b>, <b, c> }, тогда P • Q = {<a, b>}.

Композиция графика Р и  равна , то есть Р •  =  • Р = .

Если М — произвольное множество и Р  М², тогда

Р • М = М • Р = Р.

Если операцию композиции графиков сопоставить с умножением чисел, то роль нуля будет играть пустое множество, а роль единицы — диагональ ().

Пусть x, z — произвольная пара из A • B. Тогда для нее справедливо высказывание:

x, z  A • B  (y  (Y  W))(x, y  A  y, z  B).

Если некоторая пара x, z не принадлежит A • B, то истинно высказывание:

x, z  A • B  (y  (Y  W))(x, y  A  y, z  B).

В операции композиции элемент y называется компонирующим элементом для пар x, y  A и y, z  B. Если множество компонирующих элементов пусто, то и результат композиции является пустым множеством:

A • B    пр₂A  пр₁B    A •    • A  .

Приведем свойства операции композиции :

0. A • B  B • A - некоммутативность;

1. A • (B • С)  (A • B) • С - ассоциативность;

2. - дистрибутивность по объединению;

3. - дистрибутивность по пересечению;

4. (A • B)^-1  B^-1 • A^-1

Некоторые тождества следуют из определения операции композиции, остальные тождества доказываются уже известными методами.

Используя методы доказательства тождеств с множествами, можно доказать, что для любых трех графиков P, Q, R справедливо

(P • Q) • R = P • (Q • R).

Докажем это тождество:

1. Необходимость. Предположим, что существует произвольный кортеж <a, b>, принадлежащий левой части тождества. Попытаемся доказать, что он принадлежит правой части тождества.

<a, b>  (P • Q) • R  <a, z>  (P • Q) & <z, b>  R  <a, x>  P & <x, z>  Q & <z, b>  R  <a, x>  P & <x, b>  (Q • R)  <a, b>  (P • (Q • R)).

Следовательно, первая часть доказана.

2. Достаточность. Предположим, что существует произвольный кортеж <a, b>, принадлежащий правой части тождества. Попытаемся доказать, что он принадлежит левой части тождества.

<a, b>  (P • (Q • R))  <a, x>  P & <x, b>  (Q • R)  <a, x>  P & (<x, d>  Q & <d, b>  R)  <a, x>  P & <x, d>  Q & <d, b>  R  <a, d>  (R • Q) & <d, b>  R  <a, b>  ((P • Q) • R).

Следовательно, вторая часть доказана. Тогда делаем вывод, что исходное тождество справедливо.

Доказанное тождество позволяет определить композицию трех графиков P, Q, R, понимая под этим результат любой перестановки скобок, приводящей к последовательному попарному компонированию графиков. При компонировании трех графиков возможно только два способа расстановки скобок. Это позволяет определить композицию произвольного попарного компонирования графиков.

Операции композиции и инверсии связаны следующим равенством:

(P • Q)^-1 = Q^-1 • P^-1.

Докажем справедливость тождества (P • Q)^-1  P^-1 • Q^-1:

1. Необходимость. Пусть <a, b>  (P • Q)^-1  <b, a>  (P • Q)  <b, x>  P & <x, a>  Q  <x, b>  P^-1 & <a, x>  Q. Получить теперь P^-1 • Q^-1 в общем виде невозможно, следовательно, исходное тождество неверно.

Докажем теперь справедливость другого тождества (P • Q)^-1  Q^-1 • P^-1:

1. Необходимость. Пусть <a, b>  (P • Q)^-1  <b, a>  (P • Q)  <b, x>  P & <x, a>  Q  <x, b>  P^-1 & <a, x>  Q  <a, x>  Q^-1 & <x, b>  P^-1  <a, b>  (Q^-1 • P^-1).

1. Достаточность. Пусть <a, b>  (Q^-1 • P^-1)  <a, x>  Q^-1  <x, b>  P^-1  <x, a>  Q  <b, x>  P  <b, x>  P  <x, a>  Q  <b, a>  (P • Q)  <a, b>  (P • Q)^-1.

Следовательно, это тождество справедливо.

Рассмотрим два основных свойства графиков.

График Р называется функциональным, если в нем нет пар с одинаковыми первыми и разными вторыми компонентами.

Например, график Р = {<b, a>, <c, a>, <d, а>} является функциональным графиком.

На рис. 3.2 (а, б) приведены примеры функциональных графиков.

P₁ = {<a, 4>}, P₂ = {<a, 2>, <b, 3>, <c, 3>, <d, 4>}.

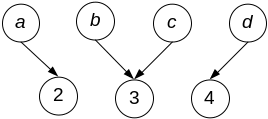
а б

Рис.3.2. Примеры функциональных графиков

График Р называется инъективным, если в нем нет пар с различными первыми и одинаковыми вторыми компонентами.

Например, Р = {<a, b>, <a, c>, <a, d>} является инъективным графиком.

На рис. 3.3 (а, б) приведены примеры инъективных графиков.

P₃ = {<a, 1>}, P₄ = {<b, 2>, <c, 3>, <c, 4>}.

а б

Рис. 3.3. Примеры инъективных графиков

Композиция функциональных графиков есть функциональный график, т.е. композиция сохраняет функциональность.

Композиция инъективных графиков инъективна. Доказательство данного утвержденияможно найти в литературе, приведенной в конце раздела.

Итак, говорят, что график P функционален тогда и только тогда, когда Р^-1 инъективен. График Р инъективен тогда и только тогда, когда Р^-1 функционален.

Примеры РЕШЕНИЯ ЗАДАЧ

Пример 3.1. Пусть заданы множества А = {a, b}; B = {3, 1, 2}; C = {, }.

Ответ: A × B × C = {a,1, , a, 1, , a, 2, , a, 2, , a, 3, , a, 3, , b, 1, , b, 1, , b, 2, , b, 2, , b, 3, , b, 3, }.

Пример 3.2. Пусть задано произвольное множество A = {a, b}. Найти третью степень заданного множества.

Ответ: A³ = A × A × A = {a, b} × {a, b} × {a, b} = {<a, a, a>; <a, a, b>; <a, b, a>; <a, b, b>; <b, a, a>; <b, a, b>; <b, b, a>; <b, b, b>}.

Пример 3.3. Доказать истинность тождества методом взаимного включения:

 × (Y  Z)  (X × Y)  (X × Z).

Доказательство:

1. Необходимость. Пусть для произвольного кортежа x, y истинно высказывание:

x, y  X × (Y  Z)  x  X  y  (Y  Z) 

(согласно свойству дистрибутивности)

x  X  (y  Y  y  Z) 

(по определению операции объединения множеств)

x  X  y  Y  x  X  y  Z 

(согласно дистрибутивному закону)

x, y  (X × Y)  x, y  (X × Z)  x, y((X × Y)  (X × Z)).

(исходя из свойства дистрибутивности)

Таким образом, прямое включение доказано.

2. Достаточность.

Аналогично доказывается обратное включение:

x, y  ((X × Y)  (X × Z))  x, y  (X × Y)  x, y  (X × Z) 

(x  X  y  Y)  (x  X  y  Z)  x  X  (y  Y  y  Z) 

x  X  y  (Y  )  x, y  ( × (Y  )).

Обратное включение доказано. Таким образом, поскольку оба включения истинны, истинно и исходное тождество.

Пример 3.4. Доказать справедливость тождества методом от противного:

((X × Y)  (W × )) \ ((X  W) × (Y  ))  .

Доказательство: Предположим, что данное выражение не верно и, следовательно, данное множество не равно пустому. Тогда должен существовать хотя бы один кортеж x, y, принадлежащий исходному множеству:

x, y  [(X × Y)  (W × Z)] \ [(X  W) × (Y  Z)] 

x, y  ((X × Y)  (W × Z)) & x, y  ((X  W) × (Y  Z)) 

согласно определению операции разности множеств)

[x, y  (X × Y) & x, y  (W × Z)] & [x  (X  W)  y  (Y  Z)] 

(согласно определению операции пересечения множеств)

(x  X  y  Y  x  W  y  Z)(x  X  x  W  y  Y  y  Z) 

(согласно дистрибутивному закону алгебры логики)

(x  X  y  Y  x  W  y  Z  x  X)  (x  X  y  Y  x  W  y  Z  x  W)  (x  X  y  Y  x  W  x  Z  y  Y)  (x  X  y  Y  x  W  y  Z  y  Z).

В полученном выражении в каждой из составляющих его конъюнкций мы обнаружили противоречие. Например, x  X  x  X. То есть очевидно, что наше предположение ложно, а значит исходное тождество истинно. Что и требовалось доказать.

Пример 3.5. Пусть задан график: А = {1, 2, 2, 3, 2, 5, 3, 4, 3, 6}. Найти его инверсию.

Ответ: А^-1 = {2, 1, 3, 2, 5, 2, 4, 3, 6, 3}.

Пример 3.6. Пусть задан график: А = {1, 2, 1, 3, 2, 3, 3, 3, 3, 4}. Найти первую и вторую проекции заданного графика.

Ответ: пр₁А = {1, 2, 3}, пр₂A = {2, 3, 4}.

Пример 3.7. Доказать справедливость тождества методом взаимного включения:

Ответ: пр₁(A  B)  пр₁A  пр₁B

Доказательство:

1. Необходимость. Предположим, что исходное высказывание справедливо, тогда для любого элемента x, принадлежащего данной проекции, справедливо следующее высказывание:

x  пр₁(A  B)  (y  Y)(x, y  (A  B)) 

x, y  A  x, y  B  x  пр₁A  x  пр₁B  x  (пр₁A  пр₁B)

согласно определению операции проектирования)

Таким образом, прямое включение доказано.

2. Достаточность. Теперь докажем, что в общем случае обратное включение невозможно. Пусть для любого x истинно:

x  (пр₁A  пр₁B)  x  пр₁А  x  пр₁В 

(y  Y)(x, y  A)  (z  Y)(x, z  B).

Поскольку в общем случае неизвестно, совпадают ли y и z, обратное включение, в общем случае, доказать невозможно.

Пример 3.8. Привести пример, демонстрирующий справедливость включения пр₁(A  B)  пр₁A  пр₁B.

Решение: Пусть заданы множества А = {1, 2}; B = {1, 3}. Очевидно, что пр₁(A  B)  пр  , в то время как пр₁A  пр₁B      .   . Таким образом, пр₁(A  B)  пр₁A  пр₁B. В случае, если A  B  , исходное высказывание преобразуется в равенство.

Пример 3.9. Привести пример того, что высказывание Пр₁А = Пр₁В  A = B - ложно.

Решение: Пусть заданы множества: А = {1, 2, 1, 3, 1, 4, 5, 6, 5, 7}; B  1, 6, 1, 7, 5, 2, 5, 3, 5, 4}.

Для доказательства построим проекции заданных множеств. Очевидно, что проекции множеств равны между собой: пр₁А = пр₁В = {1, 5}; пр₂А = пр₂В = {2, 3, 4, 6, 7}, в то время как множества A и B не равны. Следовательно, задание выполнено.

Пример 3.10. Заданы произвольные графики: А = {a, a, b, e, c, k, f, g}; B = {a, d, c, b, g, f, e, c, b, b}. Найти композиции графиков A • B и B • A.

Решение: Для того, чтобы найти композицию графиков A и B, выбираем поочередно из кортежей множества вторые компоненты A, сравниваем со всеми первыми компонентами кортежей множества B. В тех случаях, когда обнаруживается совпадение, выполняем композицию соответствующих кортежей. Например, берем вторую компоненту первого кортежа из множества A. Это компонента a. Сравниваем ее поочередно со всеми первыми компоентами кортежей множества B. Находим совпадение с первой компонентой первого кортежа множества B. В результате получаем композицию этих двух кортежей:

a, a • a, d = a, d.

Затем выбираем вторую компоненту следующего кортежа множества A и сравниваем ее со всеми первыми компонентами кортежей множества B:

b, e • e, c = b, c.

Процесс продолжается аналогично до тех пор, пока не будут выявлены все совпадения и построены все композиции кортежей. В результате мы получим композицию множеств A и B. Для построения композиции множеств B и A необходимо аналогичным образом сравнить вторые компоненты кортежей множества B с первыми компонентами кортежей множества A.

Ответ: A • B  {a, d, b, c, f, f}, B • A  {c, e, g, g, e, k, b, e}.

Пример 3.11. Доказать справедливость высказывания методом взаимного включения:

A • (B  С)  (A • B)  (A • С).

Доказательство:

1. Необходимость. Предположим, что данное тождество справедливо. Тогда существует произвольная пара:

x, z  (A • (B  С))  (y)(x, y  A  y, z  (B  С)) 

согласно определению операции композиции)

x, y  A  (y, z  B  y, z  С) 

по определению операции объединения множеств)

(x, y  A  y, z  B)  (x, y  A  y, z  С) 

согласно дистрибутивному закону

(x, z  A • B)  ( x, z  A • С)  x, z  ((A • B)  (A • С)).

То есть прямое включение доказано.

2. Достаточность. Теперь докажем обратное включение. Предположим, что существует пара:

x, z  ((A • B)  (A • С))  x, z  (A • B)  x, z  (A • С) 

(y)(x, y  A  y, z  B)  (w)(x, w  A  w, z  С) 

(так как в общем случае, компонирующие элементы не обязательно совпадают)

(x, y  A  y, z  (B  С)) (x, w  A  w, z  (B  С)) 

x, z  (A • (B  С))  x, z(A • (B  С))  x, z(A • (B  С)).

Обратное включение также доказано, следовательно, исходное тождество верно.

Пример 3.12. Доказать справедливость высказывания методом взаимного включения:

A • (B  С)  (A • B)  (A • С).

Доказательство: Доказательство прямого включения проводится аналогично доказательству, рассмотренному выше, и интереса не представляет. Рассмотрим обратное включение и докажем, что оно в общем случае не имеет места.

2. Достаточность. Предположим, что справедливо тождество:

(A • B)  (A • С)  A • (B  С).

Тогда существует произвольная пара:

x, z  ((A • B)  (A • С))  x, z  (A • B)  x, z  (A • С) 

(y)(x, y  A  y, z  B)  (w)(x, w  A  w, z  С)

(в общем случае y  w, значит продолжить цепочку преобразований, чтобы доказать обратное включение не возможно).

Таким образом, обратное включение в общем случае не доказывается.

Следовательно, высказывание A • (B  С)  (A • B)  (A • С) - истинно.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Приведите примеры кортежей.

2. Как образуется прямое произведение множеств?

3. В каком случае число элементов прямого произведения множеств равняется нулю?

4. Что представляет собой прямое произведение двух множеств с точки зрения теории множеств?

5. Какими свойствами обладает декартово произведение множеств?

6. В чем заключается операция проектирования множеств?

7. В каком случае упорядоченная пара не принадлежит прямому произведению двух множеств?

8. Для каких множеств А и В справедливо: Х × Y = Y × Х?

9. Равны ли множества: пр₁А  пр₂А и А, если: А  Х × Y?

10. Что такое инверсия упорядоченного множества А?

11. Для какого множества А  Х × Y справедливо: А=А^-1?

12. В каком случае существует композиция двух произвольных упорядоченных множеств А и В?

13. В каком случае справедливо тождество: А • В = В • А?

14. В каких случаях справедливо тождество: А • А = А?

15. Что такое график?

16. Приведите основные операции над графиками.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1. Найти прямое произведение множеств Х и Y, если:

а) Х = {{a, b}, c, {d, e, f }}; Y = {g, h};

б) Х = {а, b, c}; Y = ;

в) Х = {2, 4, }; Y = {{}, a, b}.

2. Найти n-ю степень множества Х, если:

a) Х = {x}, n = 5; в) Х = {{}, y}, n = 2;

б) Х = {a, b}, n = 3; г) Х = 0, n = 3.

3. Доказать, что для произвольных множеств Х, У, W, Z, справедливы следующие высказывания:

а) (Y  Z) × X = (Y × X)  (Z × X);

б) Х × (Y  Z) = (Х × Y)  (Х × Z);

в) Х × (Y \ Z) = (Х × Y) \ (Х × Z);

г) (Х × Y)  (W × Z)  (X  W) × (Y  Z);

д) (Х  Y) × (W  Z) = (X × W)  (Y × W)  (X × Z)  (Y × Z).

4. Равны ли множества Пр₁A  Пр₂A = A, если A  Х × Y?

5. Для каких множеств А и В, справедливо А × В = В × А?

6. Для какого множества справедливо: A = А^-1, если A Х × Y?

7. Доказать или опровергнуть, что для множеств A и B, где A  Х × Y, B  Х × Y справедливы следующие высказывания:

а) Пр₁(A \ B) = Пр₁A\ Пр₁B; д) Пр₁(A \ B) ^-1 = Пр₂A \ Пр₂B;

б) Пр₁(A  B) ^-1 = Пр₂A  Пр₂B; е) (A  B) ^-1 = А^-1  B^-1;

в) Пр₁(A  B) = Пр₂A^-1  Пр₂B^-1; ж) (A  B) ^-1 = A^-1  B^-1;

г) (A \ B) ^-1 = A^-1 \ B^-1.

8. Доказать или опровергнуть, что для множеств A, B и С, где A  Х × Y, B  Х × Y, С  Х × Y справедливы следующие тождества:

а) (B  C) • A = (B • A)  (C • A);

б) A • (B \ C) = (A • B) \ (A • C).