2.3.4 Минимизация переключательных функций с помощью диаграмм Карно-Вейча

Рассмотренные методы минимизации ПФ являются трудоемкими, т.к. при выполнении операции склеивания необходимо сравнить все возможные пары членов исходного выражения. Применение такой последовательной методики минимизации требует большого опыта и интуиции, мало наглядно, и при этом легко может возникнуть ошибка. Эти методы применимы для преобразования простых алгебраических выражений.

Существуют методы, позволяющие упростить поиск склеивающихся членов. Один из самых удобных для обычной технической практики является метод минимизации функций с использованием диаграмм Карно-Вейча. После записи логической функции в Карту Карно или диаграмму Вейча обычно сразу видна минимальная форма функции и возможность ошибки уменьшается до минимума. Карты могут быть применены и для 5-6 переменных (даже до 10), что вполне достаточно для использования в обычной практике.

Диаграмма Вейча представляет собой несколько необычную таблицу заданной ПФ. Расположение клеток этой таблицы позволяет легко определить склеивающиеся между собой члены. Склеивающиеся между собой конституенты 0 или 1 в диаграммах Вейча для функций двух переменных расположены в соседних клетках и выражаются одной буквой.

	y			y			y
x	1,1	1,0	x	x y	x	x		y
	0,1	0,0					x	x y

Диаграммы Вейча для ПФ двух аргументов

B

А	1	0	1	1
	1	1	0	1

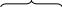
Диаграммы Вейча для ПФ трех аргументов

C

Пример. Найти минимальный ДНФ при .

Пример. Найти минимальные дизъюнктивные и конъюнктивные нормальные формы для ПФ.

B

А	1	1	1	0
	0	0	1	1

О

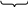
бъединить единицы можно двумя способами, дающими две минимальные дизъюнктивные формы

C

Для получения минимальной КНФ объединив нули получим:

Заметим, что минимальная КНФ содержит меньше букв, чем минимальные ДНФ.

Принцип минимизации с помощью карт Карно аналогичен предыдущему. Объединяются всегда 2 или 4 соседних поля, в которых записаны 1. Объединением двух полей исключается одна переменная, объединением четырех полей – две переменные.

Пример.

AB C
	00	01	11	10
0	1	1		1
1		1	1	1

Пример.

Применим правило де Моргана

AB C
	00	01	11	10
0	0	1	1	1
1	1	0	0	1

AB CD		B	AB	A
	00	01	11	10
00	1	1	1	1
01	0	0	1	1
11	1	1	x	x
10	1	1	x	x

1.

2.

(при дополнении по 1)

3.

(при дополнении по 0)

;

A=1 A=0

DE BC
	00	01	11	10	00	01	11	10
00	1	1	1	1			1
01					1	1	1	1
11	1	1			1	1	1	1
10	1	1		1			1