4. Динамика твердого тела
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________
Краткая теория и методические указания
Твердым телом (ТТ) называется система точек, жестко связанных между собой. Твердым можно считать любое тело, которое при решении задач нецелесообразно моделировать точкой, но форму и объем такого тела можно считать неизменным на протяжении всего времени движения.
Положение ТТ в пространстве полностью определено, если известны положение какой-либо жестко связанной с ним точки и три угла поворота тела вокруг трех взаимно перпендикулярных осей, проходящих через эту точку. Таким образом, положение ТТ определяется шестью независимыми координатами, т. е. имеется 6 степеней свободы (3 поступательные и 3 вращательные).
Обычно
движение ТТ рассматривается как
поступательное движение центра масс
ТТ и вращательное движение вокруг этой
точки О. Введем радиус-вектор
–
центр масс ТТ. Заметим, что центр масс
не обязательно совпадает с какой-либо
точкой ТТ. Тогда для центра масс можно
записать:
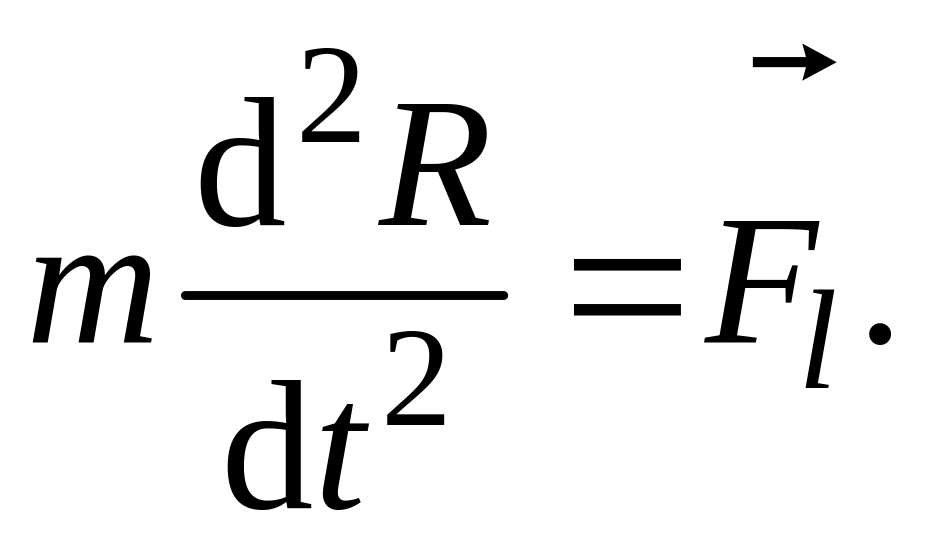(4.1)
Из него
видно, что центр масс ТТ движется как
материальная точка с массой, равной
массе
ТТ, к которой приложена равнодействующая
всех внешних сил
.
Допустим,
что, решив уравнение (4.1), нашли
.
Однако остается неизвестным, как
повернуть ТТ вокруг точки O.
Для характеристики этого поворота
введем момент импульса ТТ:
.
Для описания вращательного движения
вводится уравнение:
(4.2)
где
– сумма
моментов внешних сил.
Пусть
ТТ вращается вокруг оси
с угловой скоростью
.
Это значит, что любая точка
(кроме точек, лежащих на оси
)
имеет скорость
,
тогда как линейные скорости точек ТТ,
вообще говоря, различны. Заметим, однако,
что все они перпендикулярны оси
Проекция
момента импульса
на ось
равна
где
– угол
между радиусом-вектором
и осью
.
Введя обозначения
,
с учетом
,
получим
Сумма
,
не зависит от движения ТТ.
называется моментом инерции твердого
тела относительно оси
и зависит только от распределения массы
в ТТ. Таким образом,
,
где
– угловая скорость вращения ТТ вокруг
оси
Поскольку
при движении ТТ не изменяется, а
,
в случае вращения тела вокруг неизменной
оси (например, оси z)
,
где
– проекция
на ось z момента внешних
сил, действующих на ТТ.
Уравнения
и
можно считать уравнениями движения.
Первое из них имеет вид уравнения Ньютона
для точки. Решение второго уравнения
совместно с функцией
является законом движения твердого
тела.
Пусть
внешние силы отсутствуют, так что
и
.
Тогда
,
т. е.
.
Центр масс ТТ движется прямолинейно и
равномерно. Кроме того,
,
т. е.
.
Таким образом, в отсутствие внешних сил
твердое тело вращается, причем скорость
его вращения постоянна.
Твердое
тело в большинстве случаев можно
рассматривать как вещество, сплошь
заполняющее некоторый объем пространства.
Тогда выражение для момента инерции
относительно некоторой оси удобно
находить, разбивая ТТ на маленькие
участки объема, которые можно принять
за точки, каждая из которых имеет массу
где
– объем
участка;
– плотность,
которая, вообще говоря, является функцией
координат. Теперь момент инерции ТТ
относительно некоторой оси можно
представить в виде интеграла по объему
всего тела:
где
– расстояние
данной точки
от оси, вокруг которой происходит
вращение ТТ. Если известны плотность
массы тела в каждой точке и его
геометрические размеры, данная задача
решается путем интегрирования.