§ 6 Равноускоренное движение

Равноускоренное движение (РУД) является частным случаем неравномерного движения. Это движение, при котором скорость тела за любые равные промежутки времени изменяется на одинаковую величину. Такое движение можно пронаблюдать в жизни достаточно часто. Например, при экстренном торможении, когда блокируются все колеса автомобиля, он двигается равноускоренно. Разгон самолета по взлетной полосе, спуск санок с обледенелой горки, падение камня, начальная стадия разгона заряженных частиц в электрическом поле …- эти движения достаточно точно можно описывать, используя модель РУД.

Наша задача – определить координату тела, совершающего равноускоренное движение, в любой момент времени. Для решения поставленной задачи необходимо рассчитать проекцию перемещения тела. Проекция перемещения для любого движения численно равна площади под графиком проекции скорости. Таким образом, для решения основной задачи механики сначала необходимо выяснить зависимость скорости тела от времени.

Ускорение

Для характеристики быстроты изменения скорости вводят ускорение.

Ускорением при РУД называют отношение изменения скорости ко времени, за которое это изменение произошло.

. (6.1)

Физический смысл ускорения – это величина, численно равная изменению скорости тела в единицу времени.

Ускорение – векторная величина. Направление ускорения совпадает с направлением вектора изменения скорости .

Численное значение ускорения определяется переходом от векторов к их проекциям:

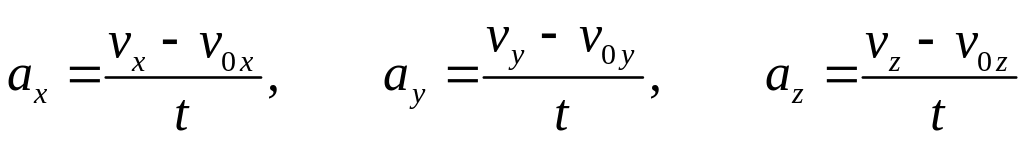. (6.2)

По знаку проекции ускорения можно судить о направлении вектора ускорения:

- вектор ускорения сонаправлен с осью ОХ .

- вектор ускорения направлен против оси ОХ .

Модуль ускорения находится через проекции .

Единицы ускорения в SI .

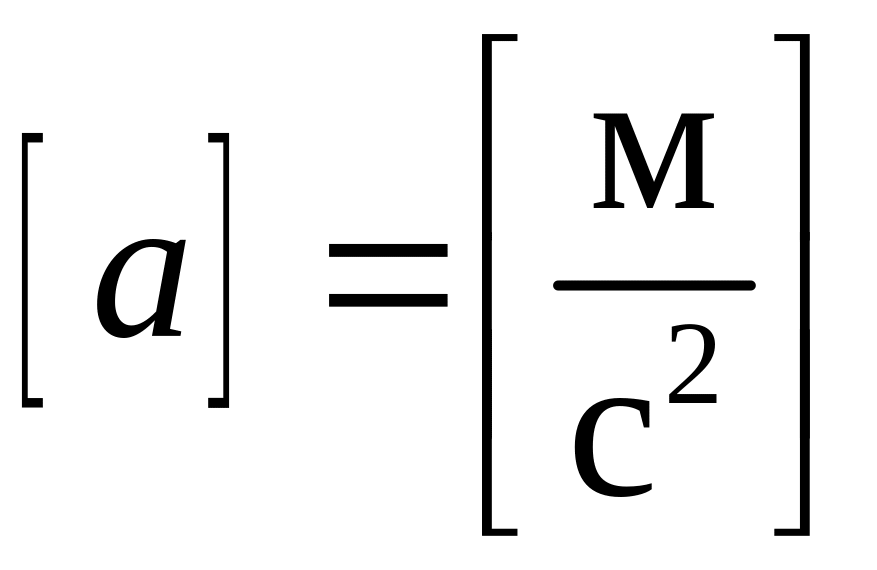Таблица 4 – Ускорения различных тел

Тело	Ускорение, м/с2
1	2
Ускорение свободного падения на Земле	9,81
Автомобиль Jeap Grand Cherokee на разгоне	до 3,4
Автомобиль при экстренном торможении	до 7
Спринтер на старте	до 5
Болид «Formula – 1»	до 11
Парашютист при раскрытии парашюта	до 70
Летчик при катапультировании	до 200
Пуля в стволе автомата Калашникова	616 000
Ракета-носитель на старте	30 – 40 (до 70)
Самолет на Ил – 62	1,7 при разбеге 2 при торможении на взлетной полосе
Продолжение таблицы 4
1	2
Скворец во время прыжка на взлете	48
Пассажирские лифты Скоростные лифты	0,3 – 0,6 0,9 – 1,6
Троллейбус	1 – 1,5 на разгоне до 5 при аварийном торможении

Например, ускорение спринтера на старте равно 5 м/c² – это значит, что за первую секунду скорость бегуна увеличивается на 5 м/с.

И з определения РУД следует, что ускорение при таком движении постоянно .

График зависимости проекции ускорения от времени представляет собой прямую, параллельную оси абсцисс.

Из уравнений (6.2) следует, что площадь прямоугольника под графиком численно равна изменению скорости тела за время t:

.

Мгновенная скорость при РУД

Уравнения (6.1) и (6.2) позволяют рассчитать скорость тела в любой момент времени:

. (6.3)

Нетрудно видеть, что зависимость мгновенной скорости от времени при РУД является линейной.

Например, скорость автомобиля изменяется по закону .

Во-первых, тело двигается вдоль оси ОХ. Зависимость линейная, следовательно, автомобиль двигается равноускоренно. Сопоставляем конкретную функцию с выражением (6.3).

Проекция начальной скорости на ось ОХ равна . Отрицательный знак означает, что вектор начальной скорости направлен против оси ОХ.

Проекция ускорения на ось ОХ равна . Положительный знак проекции означает, что вектор ускорения сонаправлен с осью ОХ.

П ростой подстановкой значений времени в уравнение убеждаемся в том, что модуль скорости автомобиля уменьшается. Таким образом, автомобиль тормозит, двигаясь против оси ОХ. Судя по численному значению ускорения, автомобиль не тормозит экстренно, блокируя все колеса, водитель слегка нажимает на педаль тормоза.

Другой пример: .

Это тело тоже двигается вдоль оси ОХ. Зависимость линейная, следовательно, тело двигается равноускоренно.

Проекция начальной скорости на ось ОХ равна . Положительный знак означает, что вектор начальной скорости сонаправлен с осью ОХ.

Проекция ускорения на ось ОХ равна . Положительный знак проекции означает, что вектор ускорения сонаправлен с осью ОХ.

Простой подстановкой значений времени в уравнение убеждаемся в том, что модуль скорости тела увеличивается. Таким образом, тело разгоняется в направлении оси ОХ.

Движение какого тела могла бы описывать такая зависимость скорости от времени? Это мог бы быть автомобиль - водитель осуществляет быстрый разгон. Таким телом может быть бегун, решивший ускориться. Разница в том, что бегун, в отличие от автомобиля, двигаться с таким ускорением длительное время не может.

Итак, при РУД тело может разгоняться или тормозить. Для определения характера движения нужно сопоставить направления (знаки проекций) векторов скорости и ускорения.

Тело разгоняется, если ускорение сонаправлено со скоростью.

Тело тормозит, если ускорение направлено против скорости.

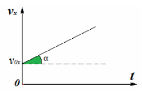
Графиком зависимости проекции скорости от времени , как для любой линейной функции, является прямая. Роль углового коэффициента линейной функции играет проекция ускорения .

Пример 1 Что можно узнать по графику зависимости проекции скорости от времени?

З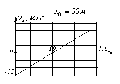 ависимость проекции скорости материальной точки от времени показана на рисунке. Определите характер движения материальной точки и ее конечную координату. Начальная координата точки . О каком тебе могла бы идти речь в задаче?

Решение:

Шаг 1 График зависимости проекции скорости от времени – прямая линия. Это означает, что зависимость скорости от времени линейная, такое возможно только при равноускоренном движении.

Шаг 2 Тело двигалось в течение 20 с. В течение первых 10 проекция скорости тела отрицательна, следовательно, тело двигалось против оси ОХ. Последующие 10 с проекция скорости тела положительна, т.е. тело двигалось в направлении оси ОХ. Т.о. в момент времени t = 10 c тело поменяло направление своего движения.

Ш аг 3 Проекция начальной скорости , конечной Проекция ускорения . На всем протяжении движения проекция ускорения положительна, следовательно, вектор ускорения сонаправлен оси ОХ.

В течение первых 10 с тело тормозило, двигаясь в направлении оси ОХ (скорость и ускорение направлены в противоположные стороны). Последующие 10 с тело разгонялось в направлении оси ОХ (скорость и ускорение сонаправлены).

Шаг 4 Перемещение при любом движении численно равно площади под графиком скорости.

Через 10 с после начала движения координата тела станет равной

Конечная координата на первом этапе движения будет начальной координатой для второго этапа. Перемещение за следующие 10 с найдем опять таки как площадь под графиком:

Перемещение при равноускоренном движении

Р ешим основную задачу механики для РУД в общем виде. Для нахождения координаты тела следует рассчитать проекцию перемещения .

Проекцию перемещения рассчитаем как площадь трапеции под графиком :

. (6.4)

Выражение (6.4) можно преобразовать, используя зависимость скорости от времени:

.

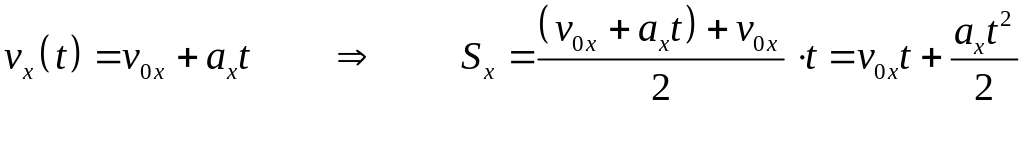. (6.5)

Выражение (6.5) интересно тем, что в него входит только одна меняющаяся величина – время t, тогда как . Таким образом, уравнение движения при РУД имеет вид

. (6.6)

Из выражения для расчета перемещения можно исключить время, опять воспользовавшись зависимостью :

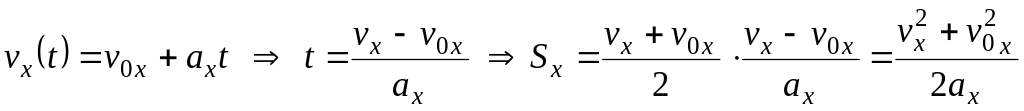
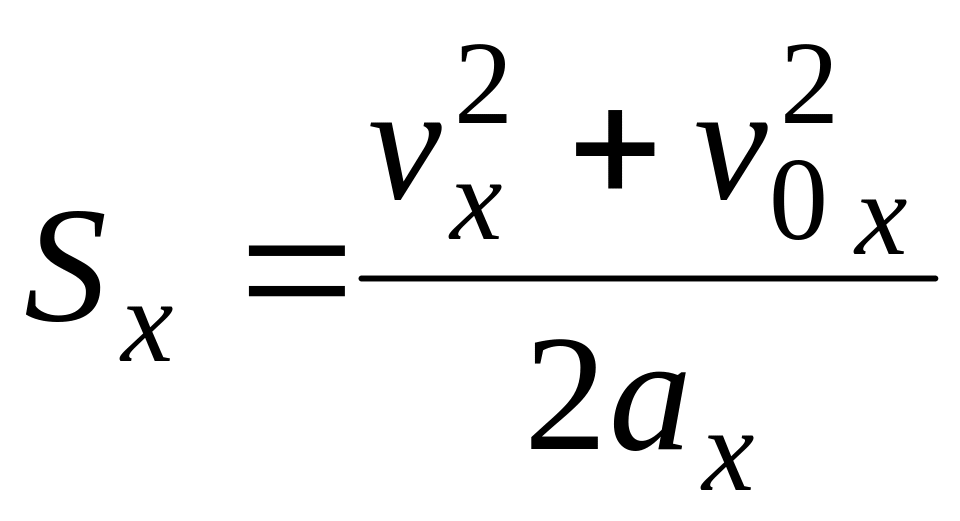. (6.7)

Мы получили соотношения между проекциями перемещения, скорости и ускорения на ось ОХ. Понятно, что все записанные выражения сохраняют свой вид при проектировании на оси ОY и OZ.

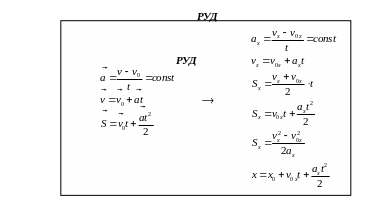
Обратите внимание на то, что все величины, характеризующие движение ( ), - векторные! Поэтому все соотношения между этими величинами записываются либо в векторной форме, либо через проекции векторов на координатные оси. Переход к модулям векторов осуществляется при решении конкретных задач.

Пример 1 Лыжник подъехал к спуску со скоростью 4 м/с. Ускорение лыжника на спуске составляет 3 м/с². На спуске лыжник не отталкивается палками и не поворачивает, как в слаломе. Запишите уравнение скорости и уравнение движения лыжника, считая ускорение постоянным на всем спуске. Как долго будет продолжаться спуск, если его длина 50 м? До какой скорости разгонится лыжник?

Р ешение:

Шаг 1 Делаем схематичный рисунок, показываем на нем вектора начальной скорости и ускорения.

Шаг 2 Выберем систему отсчета: ось координат направим вдоль горки, начало координат поместим в начало спуска. Начало отсчета времени – момент начала движения лыжника по горке.

Шаг 3 Ускорение лыжника по условию постоянно, следовательно, движение равноускоренное.

При равноускоренном движении скорость и координата тела меняются по законам

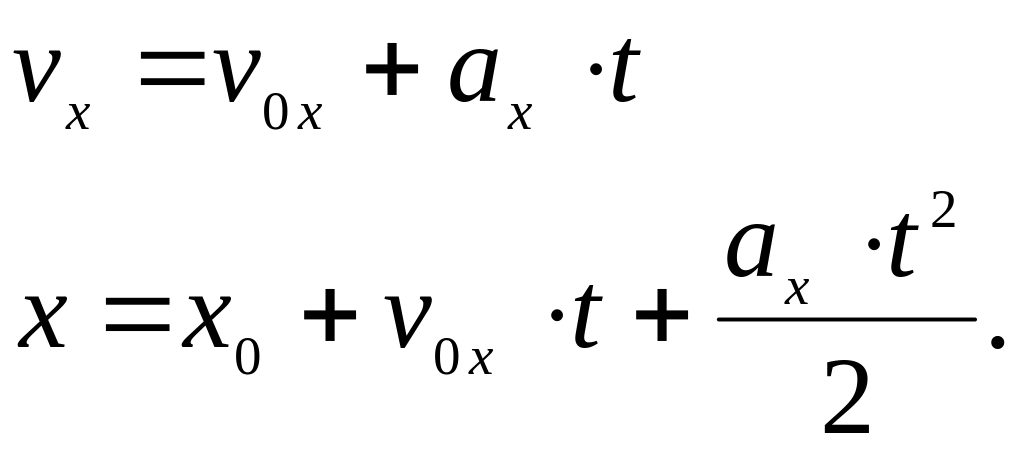
По рисунку определяем значение проекций начальной скорости, ускорения и начальную координату тела:

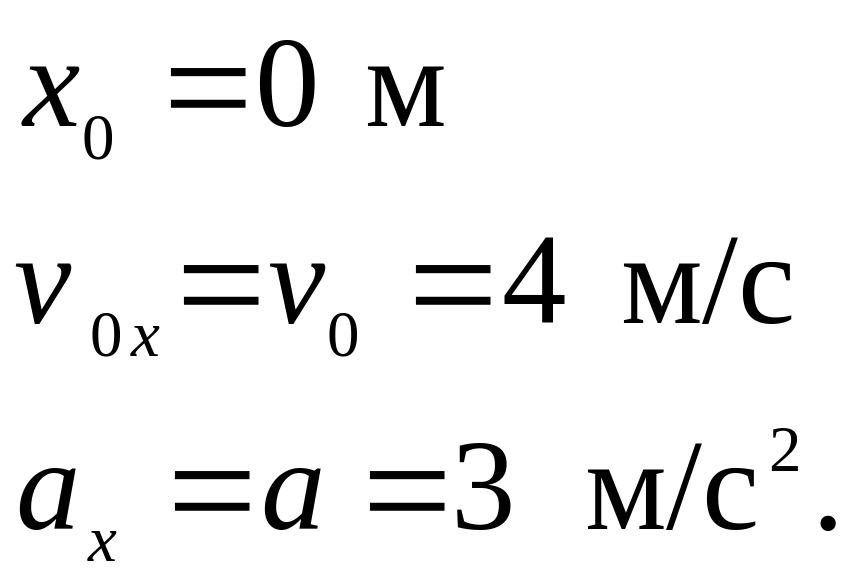
Подставляем найденные значения в выражения для расчета скорости и координаты

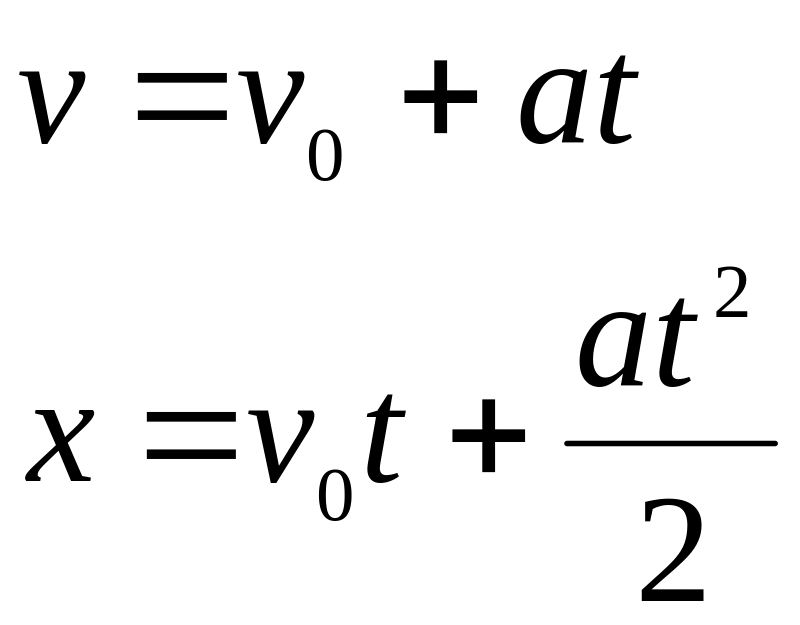
Шаг 4 Время спуска можно найти из уравнения движения

.

Координата лыжника в конце спуска равна . Подставляем численные значения координаты, скорости, ускорения в уравнение движения и решаем квадратное уравнение

,

Второй корень отрицательный, он не подходит по смыслу.

Шаг 5 Скорость в конце спуска можно определить двумя способами:

а) из уравнения для скорости ;

б) из выражения для расчета перемещения

.

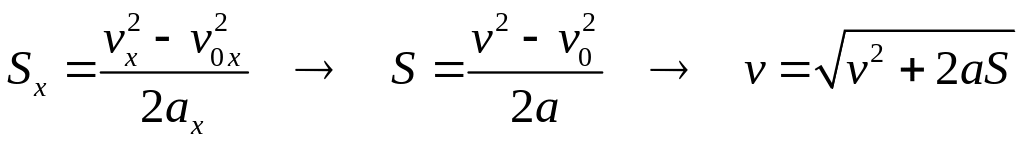Скорость в конце спуска .

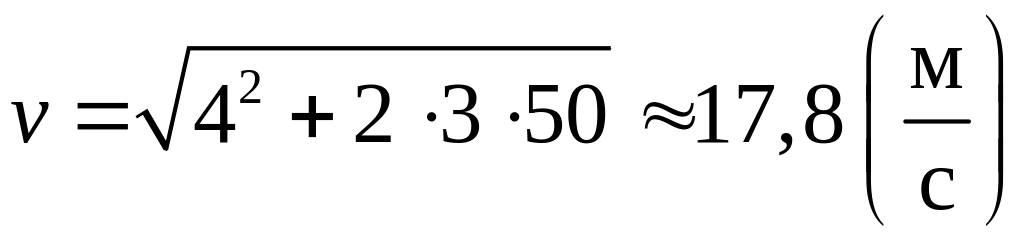Выразим эту скорость в других единицах:

С такой скоростью лыжник мог бы обгонять автомобили на улицах города (согласно правилам дорожного движения по улицам города можно ездить со скоростью, не превышающей 60 км/ч).

Пример 2 Санки толкнули по обледенелой горке вверх. На расстоянии 3 м от места начала движения санки побывали дважды – через 1 с и 3 с после начала движения. Определите начальную скорость санок и ускорение, с которым они двигались. Можно ли принять санки за материальную точку при решении этой задачи? Почему?

Замечание: Можно считать, что трение на обледенелой горке пренебрежимо мало. В этом случае ускорение тела подъеме и спуске одинаковое.

Решение:

Ш аг 1 Прямолинейное движение санок на горке является поступательным, т.е. все точки санок двигаются одинаково. В этом случае для описания движения тела можно использовать модель – материальную точку.

Делаем схематичный рисунок и выбираем систему отсчета. Координатную ось направим вдоль горки вверх. Начало отсчета времени – момент начала движения.

Шаг 2 Записываем уравнение движения и от проекций переходим к модулям в соответствии с рисунком.

.

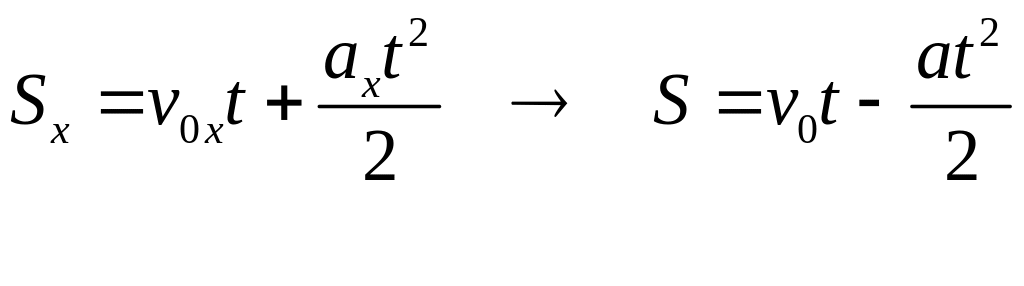Шаг 3 Записываем уравнение движения дважды – для моментов времени и . Получаем систему с двумя переменными v₀ и a .

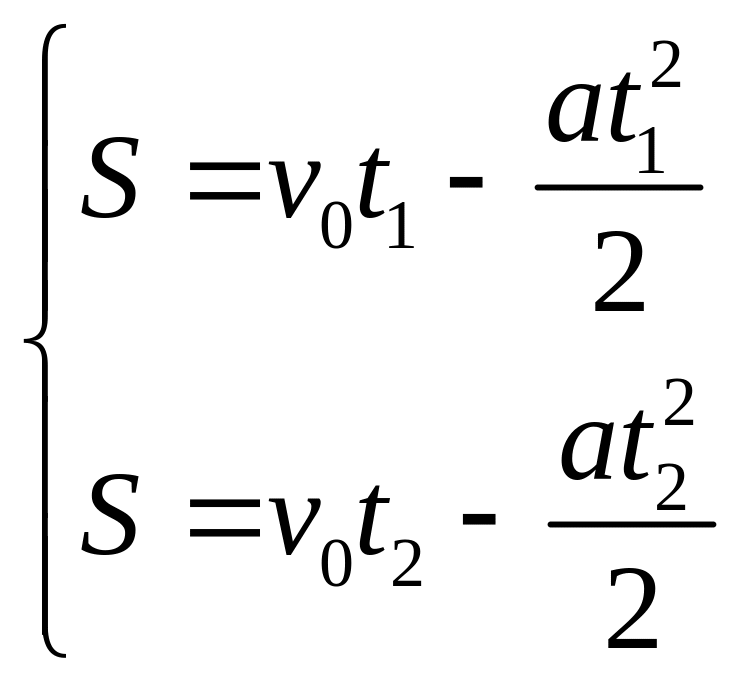
Ш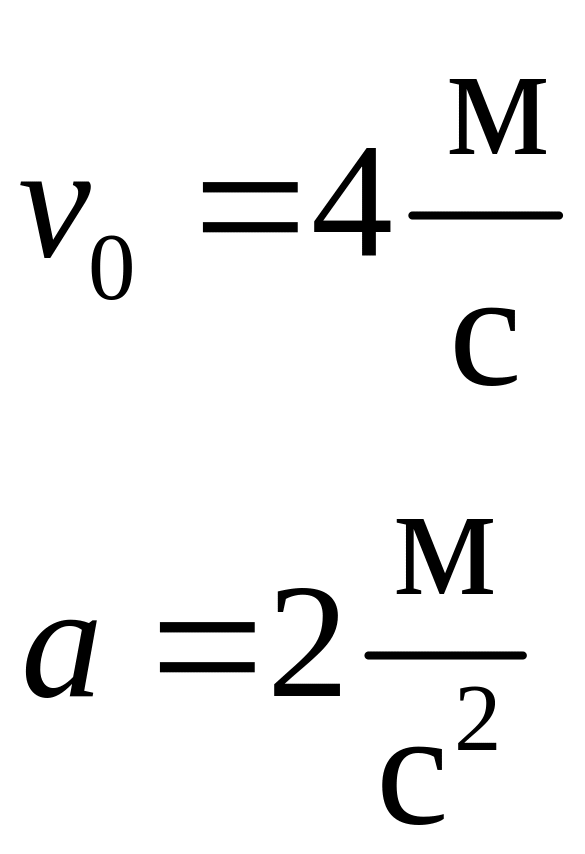 аг 4 Решаем систему и получаем для начальной скорости и ускорения значения:

Пример 3 Велосипедист совершает сложное движение. Зависимость проекции ускорения от времени показана на рисунке. Определите характер движения велосипедиста и его конечную скорость. Начальная скорость .

Решение:

Шаг 1 Велосипедист двигался в течение 6 с. Его движение можно разбить на три этапа длительностью по 2 с каждый. На первом и втором этапах ускорение тела не менялось, следовательно, на этих этапах тело двигалось равноускоренно, но с разными ускорениями. На последнем этапе ускорение равно нулю, следовательно, это равномерное движение.

Шаг 2 На первом этапе проекция ускорения . Проекции ускорения и начальной скорости имеют одинаковы положительный знак, значит оба вектора сонаправлены с осью ОХ. В течение первых 2 с велосипедист разгонялся в направлении оси ОХ. Изменение скорости движения на первом этапе движения можно найти как площадь под графиком ускорения:

.

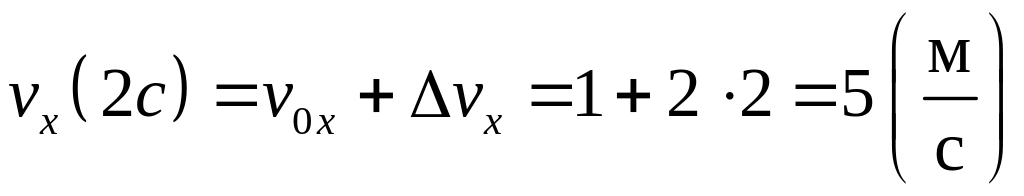Шаг 3 Конечная скорость на первом этапе – это начальная скорость для второго . Проекция ускорения на втором этапе . Видим, что начальная скорость направлена в сторону оси ОХ, а вектор ускорения – против оси ОХ. Значит, на втором этапе велосипедист тормозил, двигаясь в направлении оси ОХ (возможно, для того, чтобы не столкнуться с другим велосипедистом впереди). Изменение скорости опять-таки найдем как площадь под графиком ускорении. Это изменение теперь отрицательно, ибо график ускорения расположен ниже оси абсцисс:

Шаг 4 Последние 2 с тело совершало равномерное движение в направлении оси ОХ со скоростью 3 м/с. График изменения проекции скорости тела от времени показан на рисунке.

П ример 4 Скорость тела менялась со временем так, как показано на рисунке. По графику зависимости проекции скорости от времени постройте зависимость координаты тела от времени, если начальная координата тела равна .

Решение:

Шаг 1 Тело двигалось вдоль оси ОХ в течение 11 с. Определим характер движения тела на отдельных этапах.

Первый этап – от нуля до 3 с – торможение в направлении оси ОХ ( > 0, < 0).

Момент времени t = 3 c – тело остановилось.

Второй этап – от 3 с до 5с – разгон из состояния покоя против оси ОХ.

Третий этап – от 5 с до 8 с – равномерное движение против оси ОХ со скоростью 4 м/с.

Ч етвертый этап – от 8 с до 11 с – торможение против оси ОХ ( < 0, > 0). В момент времени t = 11 c – тело остановилось.

Шаг 2 Находим проекции перемещения на каждом из этапов как площадь по графиком скорости. Если график расположен ниже оси абсцисс, то проекция перемещения отрицательная.

Шаг 3 Рассчитываем координату тела в конце каждого этапа. Конечная координата на одном этапе является начальной для следующего

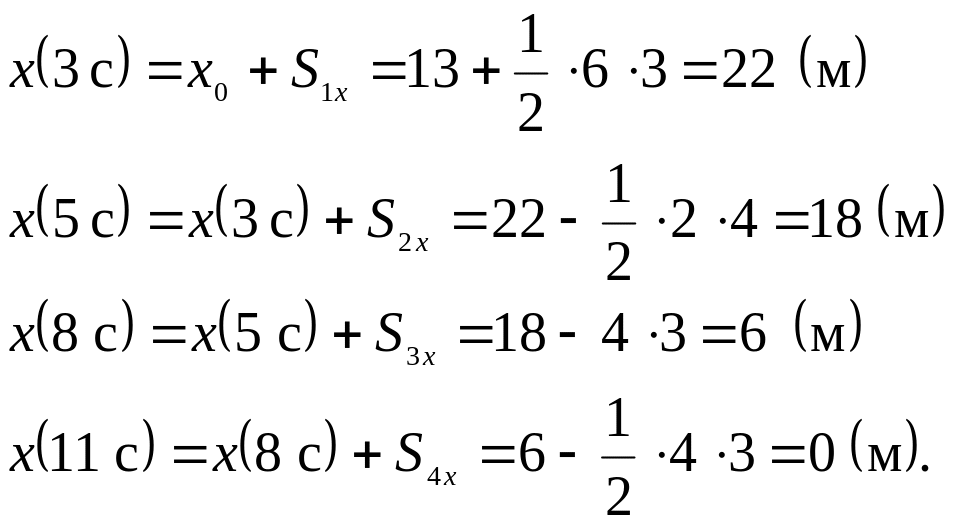
Шаг 4 Переносим ключевые моменты времени с графика для скорости на график координаты и отмечаем положение тела в эти моменты времени.

Шаг 5 Соединяем полученные точки.

Участок 0 с – 3 с – 5 с - парабола. При t = 3 с, в момент остановки, у параболы должна быть вершина (угол наклона касательной к графику координаты должен быть равен нулю, ибо ).

Участок 5 с - 8 с - прямая, ибо движение на этом участке пути равномерное.

Участок 8 с – 11 с - парабола. В момент останови t = 11 с у параболы должна быть вершина.

Контрольные вопросы

1 Выберите правильное определение равноускоренного движения

А) РУД – это движение, при котором перемещение тела меняется на одинаковую величину за любые равные промежутки времени.

Б) РУД – это движение, при котором скорость тела меняется на одинаковую величину за любые равные промежутки времени.

В) РУД – это движение с меняющейся скоростью.

Г) РУД – это движение, при котором скорость тела увеличивается на одинаковую величину за любые равные промежутки времени.

2 Как рассчитать мгновенную скорость при равноускоренном движении?

А) ; Б) ; В) ; Г) .

3 Как выглядит уравнение движения при равноускоренном движении?

А) ; Б) ;

В) ; Г) .

4 Сформулируйте условия разгона и торможения. Выберите рисунок, иллюстрирующий это условие.

Тело разгоняется, если…		рисунок
Тело тормозит, если …		рисунок

А) …когда начальная конечная скорости сонаправлены;

Б) …когда начальная и конечная скорости направлены в противоположные стороны;

В) …когда ускорение сонаправлено со скоростью;

Г) …когда ускорение направлено против скорости;

Д) … когда ускорение тела положительное;

Е) …когда ускорение тела отрицательное.

5 Уравнение движения автомобиля после того, как включился красный сигнал светофора, выглядит следующим образом: . Какой из рисунков соответствует задаче?

6 Установите соответствие между уравнением движения тела и рисунком, на котором это движение изображено.

7 Заданы уравнения зависимости скоростей от времени для четырех тел. Определите характер движения каждого тела.

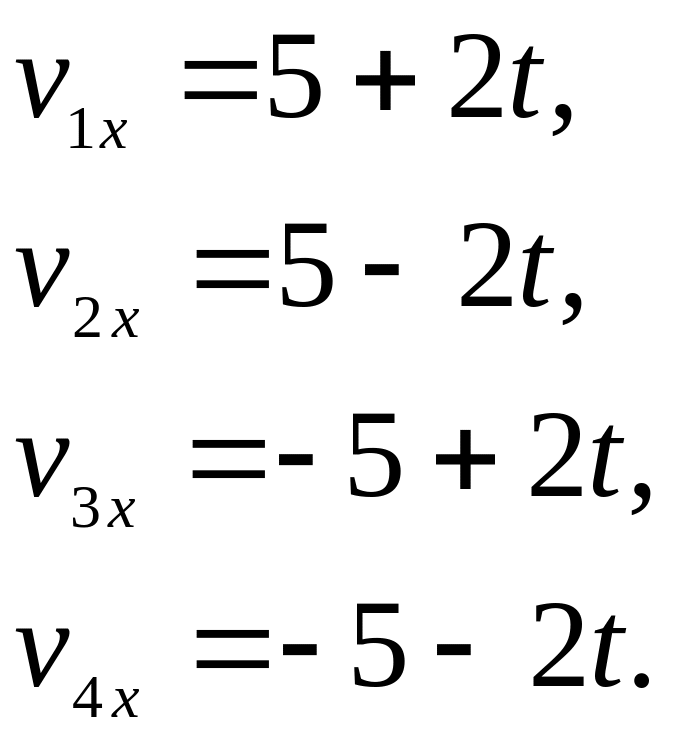
Замечание: считать, что численные значения всех величин указаны в СИ

Задания для самостоятельного движения