Практикум «Равномерное движение» Вариант 1

1 Опишите характер движения тел. Все величины в уравнениях указаны в SI. Сделайте пояснительный рисунок.

• x = 5 t - 8;

• x = 3 + 4 t;

• x = - 10 t.

2 Расстояние между станциями А и В равно 46 км. От станции А отправляется пассажирский состав со скоростью 72 км/ч. Через 15 мин после выхода пассажирского поезда от станции В в том же направлении отправляется товарный состав со скоростью 56 км/ч. Где и когда пассажирский поезд догонит товарный?

3 По графикам записать уравнения движения тел, определить характер их движения, найти время и место встречи.

4 По графику зависимости проекции скорости от времени постройте график зависимости координаты тела от времени, если х₀ = - 1 м.

Вариант 2

1 Опишите характер движения тел. Сделайте пояснительный рисунок. Все величины в уравнениях выражены в SI.

• x = 2 t - 7;

• x = 10 - 5 t;

• x = 6 t.

2 Между населенными пунктами А и В расстояние 56 км. Из В в А отправился рейсовый автобус со скоростью 52 км/ч. Через 10 мин навстречу ему из пункта А выехал автомобиль со скоростью 90 км/ч. Где и когда автомобиль встретится с автобусом?

3 По графикам зависимости координаты тел от времени записать уравнения движения, описать характер движения тел, найти время и место их встречи.

4 По графику зависимости проекции скорости тела от времени постройте

график зависимости координаты тела от времени., если х₀ = 2 м.

§ 5 Неравномерное движение

Большинство движений, наблюдаемых в природе, не являются равномерными.

Задача остается прежней – определить положение тела в любой момент времени. При решении основной задачи механики задачи для РД потребовалось ввести величину, характеризующую быстроту движения – скорость. Попробуем применить аналогичный прием к расчету неравномерного движения.

1 Средняя скорость – это отношение всего перемещения ко времени, за которое оно было совершено.

. (5.1)

Средняя скорость – векторная величина. Направление средней скорости совпадает с вектором перемещения тела.

Зная среднюю скорость, можно определить все перемещение или все время движения. Однако определить положение тела в любой момент времени невозможно.

Более того, встречаются и такие ситуации: если тело вернулось в исходную точку, его перемещение равно нулю , значит, и средняя скорость равна нулю . Создается впечатление, что тело покоилось, тогда как в действительности оно двигалось.

2 Средняя путевая скорость – это отношение всего пути ко всему времени движения.

_(5.2)

В отличие от средней скорости средняя путевая скорость – скалярная величина. Численные значения этих скоростей в общем случае не совпадают, поскольку длина вектора перемещения и длина траектории (пройденный путь) одинаковы только для прямолинейного движения в одном направлении. Во всех остальных случаях пройденный путь и длина траектории не совпадают.

Средняя путевая скорость не позволяет определить положение тела в любой момент времени. Например, длина автобусного маршрута «Станция метро «Красногвардейская» - аэропорт Домодедово» составляет 26,8 км, время автобуса в пути 60 мин. Средняя путевая скорость автобуса составляет 26,8 км/ч. Это не значит, что через 12 минут после отправления автобус проедет путь 5,36 км! Через 2 минуты после отправления автобус мог попасть в пробку и в течение следующих 10 мин не двигаться.

Таким образом, зная среднюю путевую скорость, можно рассчитать только весь путь или все время движения,

3 Мгновенная скорость – скорость тела в данный времени в данной точке траектории.

Сказанное выше еще не является определением мгновенной скорости, поскольку нет указания на математические действия, позволяющие рассчитать мгновенную скорость.

Математически определить мгновенную скорость возможно благодаря важному свойству механического движения – оно непрерывно. Это означает, что координата тела не может изменяться скачком. Перемещаясь из одной точки в другую, тело обязательно проследует все точки какой-то линии, соединяющей начальное и конечное положение. Непрерывность - отличительная черта движения в классической механике. В микромире о ряде очевидных для нас явлений придется забыть.

Для нахождения скорости тела в точке А выберем участок траектории ВС, содержащий точку А. За время движения от В до С тело совершило перемещение .

Рассчитаем среднюю скорость на участке ВС: . Найденная таким образом скорость может существенно отличиться от скорости тела в точке А.

Сократим участок траектории, содержащий точку А. Одновременно сократится и время прохождения этого участка. Рассчитаем среднюю скорость на участке DE: . Эта скорость опять же далека от скорости в точке А. Но в сравнении с первым результатом, вновь найденная скорость ближе к значению скорости в точке А.

Понятно, что сокращая участок траектории, содержащий интересующую нас точку, и время его прохождения, мы получаем значение средней скорости, все более приближающееся к скорости в точке А.

В математике в этом случае говорят, что у последовательности есть предел – в нашем случае это скорость тела в точке А:

(5.3)

По определению перемещение - это изменение радиус-вектора. Определение средней скорости принимает вид

(5.4)

В математике такое действие называется производной. Таким образом, мгновенная скорость – это производная от радиус-вектора по времени. Выражение (5.4) в математике принято записывать в виде

(5.5)

Эта запись отражает суть проведенной нами операции по введению понятия мгновенной скорости. Под символом можно понимать малый интервал времени (в математике говорят «стремящийся к нулю» ), – малое перемещение за время .

Обратите внимание, мгновенная скорость неравномерного движения по существу определяется как при равномерном движении – это отношение перемещения ко времени. Действительно, за малый промежуток времени изменением скорости можно пренебречь и считать движение равномерным. По существу, разбивая неравномерное движение на малые промежутки времени, мы сводим его к последовательности участков, на которых тело двигалось равномерно. Именно таков принцип работы ряда автомобильных спидометров, использующих систему спутникового позиционирования GPS – электронным путем определяются пройденный автомобилем путь и время. Для нахождения мгновенной скорости остается разделить путь на время.

Мгновенная скорость – векторная величина. Направление скорости должно совпадать с направлением вектора перемещения . Ввиду своей малости перемещение сливается с траекторией. Значит, вектор мгновенной скорости в любой точке направлен по касательной к траектории.

Численное значение мгновенной скорости, как правило, определяется переходом от векторов к их проекциям:

. (5.6)

Проекции мгновенной скорости на координатные оси являются производными от соответствующих координат. В выражениях (9) - это малые перемещения по координатным осям или малые изменения координат за время .

Модуль мгновенной скорости можно найти либо через проекции, либо как производную от пройденного пути l:

Численное значение мгновенной скорости можно определить по графику зависимости координаты тела от времени.

Для нахождения мгновенной скорости в момент времени t необходимо малое изменение координаты разделить на промежуток времени . Нетрудно видеть, что отношение - не что иное, как тангенс угла α. Таким образом, для определения проекции мгновенной скорости необходимо определить тангенс угла наклона касательной к графику в интересующий нас момент времени.

Мгновенная скорость позволяет решить основную задачу механики для неравномерного движения.

Малое перемещение по оси ОХ можно найти как при РД, умножив скорость на время:

Для нахождения всего перемещения нужно просуммировать все малые перемещения:

. (5.7)

Координата тела в произвольный момент времени t может быть рассчитана как

. (5.8)

Операцию суммирования малых перемещений можно выполнить графически.

Разбиваем все время движения на малые промежутки времени . За малое время изменением скорости можно пренебречь и считать движение равномерным. При РД перемещение численно равно площади под графиком скорости. Таким образом, малое перемещение по оси ОХ численно равно площади полоски ABCD. Для нахождения перемещения за время t нужно просуммировать все , т.е. просуммировать площади всех полосок. Сумма площадей всех полосок дает площадь под графиком проекции скорости за время t.

Таким образом, при любом движении проекция перемещения численно равна площади фигуры под графиком зависимости проекции скорости от времени.

Примеры решения задач

Пример 1 Турист отправился из лагеря к лесному озеру. Треть времени он шел по просеке со скоростью 5 км/ч. Оставшееся время он пробирался по лесной тропинке со скоростью 2 км/ч. Чему равна средняя путевая скорость туриста от лагеря до озера?

Решение:

Шаг 1 Весь путь состоит из двух частей

Тогда средняя скорость

Шаг 2 Путь на первом участке пути

Путь на втором участке пути

Шаг 3 Подставляем значения путей в выражение для средней скорости

Шаг 4 Подставляем численные значения

(км/ч).

Анализ результата

Обратите внимание, что среднюю скорость нельзя искать как среднее арифметическое скоростей на отдельных участках траектории!

Среднюю скорость можно находить как среднее арифметическое в том случае, когда все время движения разбито на равные по длительности интервалы времени.

Пример 2 Велосипедист выехал из города в деревню. Треть пути он ехал по горизонтальному шоссе со скоростью 11,5 км/ч. Оставшийся путь был подъемом, поэтому скорость пришлось сбавить до 7 км/ч. Определите среднюю путевую скорость велосипедиста во время тренировки.

Решение:

Шаг 1 Все время движения велосипедиста разбито на две части – движение по шоссе и подъем _.

Тогда средняя скорость

Шаг 2 Время движения по шоссе

Время подъема

Шаг 3 Подставляем значения времен движения на отдельных участках в выражение для средней скорости

Подставляем численные значения (км/ч).

Пример 3 На рисунке показана зависимость координаты тела от времени. Сравните скорости тела в моменты времени и .

Решение:

Шаг 1 По определению проекция мгновенной скорости – это производная от соответствующей координаты тела. . Геометрический смысл производной – тангенс угла наклона касательной к графику функции. Следовательно, для сравнения скоростей нужно сравнить углы наклона касательных в точках графика, соответствующих моментам времени и .

Шаг 2 Находим точки графика, соответствующие моментам времени и . Проводим касательные к графику в этих точках.

Шаг 3 Сравниваем углы наклона касательных.

< < <

Пример 4 Биолог исследует суточную активность муравьев. Один из муравьев бежит вдоль ствола дерева. На рисунке показана временная зависимость проекции скорости муравья на ось ОХ, проеденную вдоль ствола и направленную вверх.

Каков характер движения насекомого? Определите путь и перемещение муравья за время наблюдения. Чему равны модуль средней скорости и средняя путевая скорость муравья.

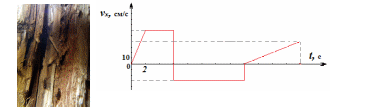
Решение:

Шаг 1 Движение муравья разбито на три этапа. В течение первых 2 с муравей разгонялся в направлении оси ОХ до скорости 60 cм/с, следующие 4 секунды бежал равномерно в том же направлении. В момент времени t = 6 с муравей наткнулся на семечку и с грузом отправился обратно. В момент времени t = 16 с оставил семечку в муравейнике и поспешил, разгоняясь, в первоначальном направлении вверх. Общее время наблюдения составило 24 с.

Ш аг 2 Проекция перемещения на каждом этапе численно равна площади под графиком скорости.

см,

см,

см.

Общее перемещение найдем как сумму проекций перемещений на отдельных участках

Шаг 3 Пройденный путь – длина траектории. Поскольку движение на каждом их этапов было прямолинейным, путь на отдельных этапах равен модулю перемещения. Тогда весь пройденный муравьем путь равен

Шаг 4 Проекцию средней скорости находим как отношение проекции перемещения ко времени

Среднюю путевую скорость находим как отношение всего пройденного пути ко времени

Понятно, что значение средней путевой скорости в большей степени характеризует напряженный образ жизни муравьев.

Задания для самостоятельного решения

1 Какие тела двигаются неравномерно?

А) Тележка с капельницей, изображенная на рисунке;

Б) стрелка часов;

В) поезд, следующий от Воронежа до Москвы;

Г) шарик, тонущий в воде;

Д) парашютист после раскрытия парашюта;

Е) стрела, выпущенная вверх.

2 На рисунках показаны зависимости скоростей тел от времени. Какие из тел двигаются неравномерно?

3 На рисунках показаны зависимости координат тел от времени. Какие из тел двигаются неравномерно?

4 Водитель Бубликов вывел свой автобус из гаража на маршрут в 6.00 ч. В 15.00 ч он вернулся обратно после окончания смены. Показания счетчика километров за это время увеличились на 360 км. Чему равны средняя и средняя путевая скорости автобуса в этот день?

5 Чему равны средняя и средняя путевая скорости конца минутной стрелки за полчаса? Длина стрелки 10 см.

6 Скорый поезд Оренбург – Москва находится в пути 27 ч. Расстояние между Москвой и Оренбургом 1500 км. Какой путь пройдет поезд через 2 часа после отправления со станции Оренбург?

А) 111 км;

Б) примерно 111 км;

В) точный ответ дать невозможно, т.к. длина состава неизвестна;

Г) ответ дать невозможно, т.к. средняя скорость позволяет рассчитать только все время движения или весь путь.

7 Собака убежала от своего хозяина на расстояние 100 м за 8,4 с, потом за треть этого времени она пробежала половину пути обратно. Вычислите среднюю и среднюю путевую скорости собаки.

8 В квалификационных заездах автогонщик должен на протяжении четырех кругов показать среднепутевую скорость 200 км/ч. Из-за сбоев в двигателе среднепутевая скорость на первых двух кругах оказалась равной 170 км/ч. С какой средней скоростью гонщик должен пройти последние два круга?

9 Экспедиция, отправившаяся в горы для проведения научных исследований, проделала путь l₁ = 20 км по предгорной равнине, двигаясь при этом со скоростью υ₁ = 5 км/ч, а затем по горной дороге еще l₂ = 4 км со скоростью υ₂ = 2 км/ч. Определите среднюю путевую скорость движения экспедиции.

10 Группа туристов москвичей решила посетить Ярославль, до которого они поедут на машине. Путь состоит из двух больших участков. Первый участок: Москва–Переяславль-Залесский протяженностью S₁ = 130 км, второй: Переяславль-Залесский–Ярославль протяженностью S₂ = 120 км. Средняя скорость движения автомобиля на первом участке равна υ₁ = 65 км/ч, на втором участке равна υ₂ = 80 км/ч. Определите среднюю путевую скорость на всем пути.

11 Добираясь от лагеря до сторожки лесника, туристы двигались по равнине на север в течение 2 часов со средней скоростью 4 км/ч. Затем туристы повернули на запад и преодолели лесной участок протяженностью 6 км за 4 часа. Чему равны средняя и средняя путевая скорости туристов при переходе от лагеря до сторожки?

12 Спортсмен пробегает на тренировке 2 км за 5 минут, а затем, не спеша, возвращается в исходную точку за 10 минут. Какова средняя путевая скорость движения в течение первых 5 минут? Какова средняя скорость прохождения всего пути?

13 Машина движется в одном направлении со средней скоростью 80 км/ч в течение 2,5 часов, а затем со скоростью 40 км/ч в течение 1,5 часа. Какова средняя путевая скорость движения за 4 часа?

14 Автобус выходит из пункта А и проходит расстояние 40 км до пункта В со скоростью 40 км/ч, затем останавливается в пункте в на 20 минут и возвращается в пункт А со скоростью 60 км/ч. Найдите среднюю и среднюю путевую скорость автобуса за все время движения.

15 Половину времени движения из пункта А в пункт В автобус двигался со скоростью 60 км/ч, вторую половину времени – со скоростью 40 км/ч. Какова средняя путевая скорость автобуса при движении между пунктами А и В?

16 Половину пути от пункта А до пункта В автобус двигался со скоростью 60 км/ч, вторую половину пути – со скоростью 40 км/ч. Какова средняя путевая скорость автобуса при движении между пунктами А и В?

17 Первую треть пути турист двигался со скоростью 6 км/ч, вторую треть – со скоростью 2 км/ч, последнюю треть - со скоростью 3 км/ч. Какова средняя скорость туриста на маршруте?

1 8 Автомобиль проходит 50 км со скоростью 40 км/ч. С какой скоростью он должен проходить следующие 50 км, чтобы средняя скоростью движения на 100 – километровом участке составила 50 км/ч?

19 Треть времени велосипедист двигался со скоростью 20 км/ч. Какой была скорость в течение оставшегося времени, если средняя скорость на всем участке траектории составила 16 км/ч?

20 На графиках показана зависимость координаты тел от времени. Рассчитайте перемещение тел за все время движения.

При некотором масштабе график зависимости проекции скорости от времени представляет собой половину окружности.

21 Как направлена мгновенная скорость? Выберите рисунок, на котором правильно указано направление мгновенной скорости.

А Мгновенная скорость направлена по касательной к траектории;

Б Мгновенная скорость сонаправлена с полным перемещением тела;

В Мгновенная скорость – скалярная величина, у нее нет направления;

Г Мгновенная скорость направлена к центру кривизны траектории.

22 Автобус движется в течение 20 с по прямой до полной остановки, проходя при этом расстояние 310 м. Его начальная скорость 15 м/с. Докажите, что часть времени автобус разгонялся.