§ 4 Графическое изображение движения

Физические процессы достаточно часто изображают графически, это проследить динамику изменения величин, характеризующих процесс.

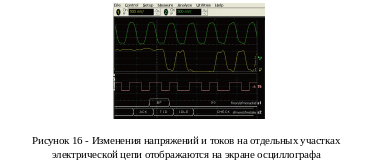
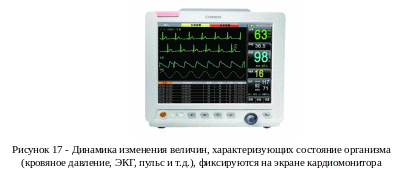
При описании механического движения графически изображают зависимости скорости и координаты тела от времени.

При РД скорость постоянна, следовательно, графиком временной зависимости проекции скорости является прямая, параллельная оси абсцисс, по которой откладывают время.

П ример 1 График при равномерном движении

На рисунке показана зависимость проекций скорости двух тел от времени. Определите характер движения тел, направление их движения, запишите уравнения движения. Какие перемещения совершат тела за 5 с? Запишите уравнения движения тел, если их начальные координаты равны и .

Решение:

1 Из рисунка видим, что проекции скоростей обоих тел не меняются с течение времени. Следовательно, оба тела двигаются равномерно вдоль оси ОХ.

2 Тела пришли в движение одновременно.

3 Проекция скорости первого тела положительная, значит, вектор скорости первого тела сонаправлен с осью ОХ. Первое тело двигается в направлении оси ОХ.

4 Проекция скорости второго тела отрицательна, значит, вектор скорости второго тела направлен против оси ОХ. Второе тело двигается протии оси ОХ.

5 Уравнения движения тел (м), (м).

6 Перемещения за 5 с могут быть найдены двумя способами – аналитически или графически.

Проекция перемещения при равномерном движении может быть рассчитана как

(м)

(м).

С другой стороны, проекция перемещения может быть найдена как площадь под графиком проекции скорости.

При этом следует помнить, что площади приписывается знак «-», если график проекции скорости располагается ниже оси абсцисс.

Очевидно, результат совпадает с расчетами, полученными аналитически.

Пример 2 График при равномерном движении

Зависимость координаты тела от времени при РД является линейной функцией . Графиком такой зависимости является прямая.

Когда полезно построить такой график? Например, при изучении движения космических объектов – звезд, планет, комет, астероидов. По графикам можно определять скорости объектов, предсказывать их движение.

Н а графике показана зависимость координаты от времени для трех тел. Опишите их движение: определите характер движения тел, начальные координаты и координаты тел через 4 с после начала движения, скорости, направление движения, запишите уравнение движения каждого тела.

Решение:

1 Графики - прямые линии, следовательно, зависимости координат от времени для всех трех тел являются линейными функциями. Это может быть только при равномерном движении.

2 Тела пришли в движении одновременно из точки с начальной координатой .

3 Координаты тел в момент времени 4 с определим непосредственно из графика:

м;

м;

м.

4 Рассчитаем проекции скоростей тел. При равномерном движении проекция скорости равна

Для нахождения проекции скорости нужно определить координату тела в любой момент времени. Мы уже сделали это для t = 4 с. Тогда

(м/с),

(м/с),

(м/с).

5 Направления движения можно определить двумя способами: аналитически и графически.

Проекции скоростей первого и второго тел положительны. Скорости этих тел сонаправлены оси ОХ, первое и второе тела двигаются в направлении оси ОХ.

Рассчитанная ранее проекция скорости третьего тела отрицательна, следовательно, это тело двигается против оси ОХ.

Можно было обойтись без расчетов проекций скоростей. Проекция скорости в линейной функции является угловым коэффициентом, т.е. , где - угол между графиком скорости и положительным направление оси абсцисс. Если угол наклона графика скорости к положительному направлению оси абсцисс острый, то угловой коэффициент положительный. Такое тело двигается в направлении оси ОХ.

Если угол наклона графика скорости к положительному направлению оси абсцисс тупой, то угловой коэффициент отрицательный. Такое тело двигается против направления оси ОХ.

Кстати, сравнивая углы наклона графиков, можно без дополнительных расчетов определить, у какого из тел скорость наибольшая – наклон графика к оси абсцисс для этого тела самый большой. У тела с наименьшей скоростью наклон графика к оси абсцисс самый маленький.

6 Общий вид уравнения движения при равномерном движении . Подставляем значения начальной координаты и найденной проекции скорости:

(м);

(м);

(м).

Пример 3 Построение графика по графику

Известна зависимость координаты тела от времени. Постройте зависимость проекции скорости этого тела от времени.

Решение:

Шаг 1 Определяем характер движения тела

График состоит из трех прямолинейных участков. Следовательно, на каждом из этих участков тело двигалось равномерно. На втором участке координата тела не меняется, это значит, что в интервале от 3 с до 6 с тело не двигалось.

Продолжительность этапов

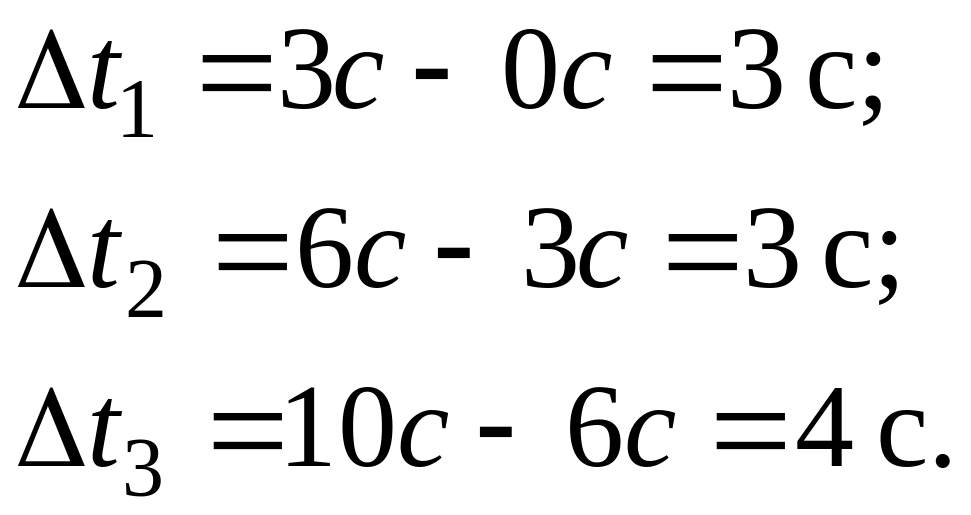
Шаг 2 Определяем проекцию скорости на первом и третьем этапах движения

Для равномерного движения .

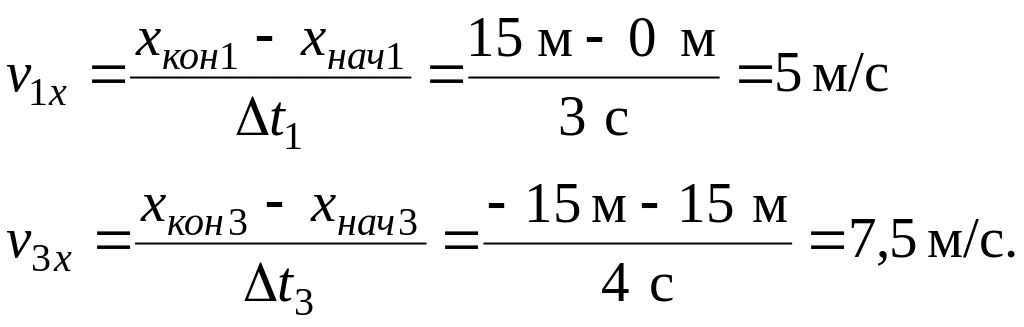
Шаг 3 Строим график зависимости проекции скорости от времени

Обратите внимание, как пограничные моменты времени перенесены с одной координатной плоскости на другую.

Пример 4 Построение графика по графику

На графике показана зависимость проекции скорости шайбы от времени. Постройте зависимость координаты шайбы от времени, если ее начальная координата . Смоделируйте ситуацию по предложенному графику. Например, на хоккейном поле…

Решение:

Шаг 1 Определяем характер движения тела

Видим, что движение состояло из трех этапов, продолжительностью по 3 с каждый. На каждом из этапов численное значение скорости тела не менялось. Следовательно, на каждом из этапов в отдельности тело двигалось равномерно.

Шаг 2 Определяем проекции перемещения тела на каждом из этапов как площадь под графиком скорости.

Шаг 3 Рассчитываем координату тела в конце каждого участка.

(м)

(м)

(м).

Шаг 4 Строим зависимость координаты тела от времени. Для этого:

• П ереносим моменты изменения скорости с одной координатной плоскости на другую.

• Отмечаем положение тела в эти моменты времени.

• Соединяем отмеченные точки прямыми линиями, ибо при равномерном движении зависимость координаты от времени – линейная.

События на хоккейном поле могли развиваться следующим образом: игрок сборной России ведет шайбу в сторону канадских ворот в течение 3 с, делает передачу товарищу по команде, тот продолжает движение в сторону ворот противника. В момент времени 6 с канадцы перехватывают шайбу и начинают контратаку…

З адания для самостоятельного решения

1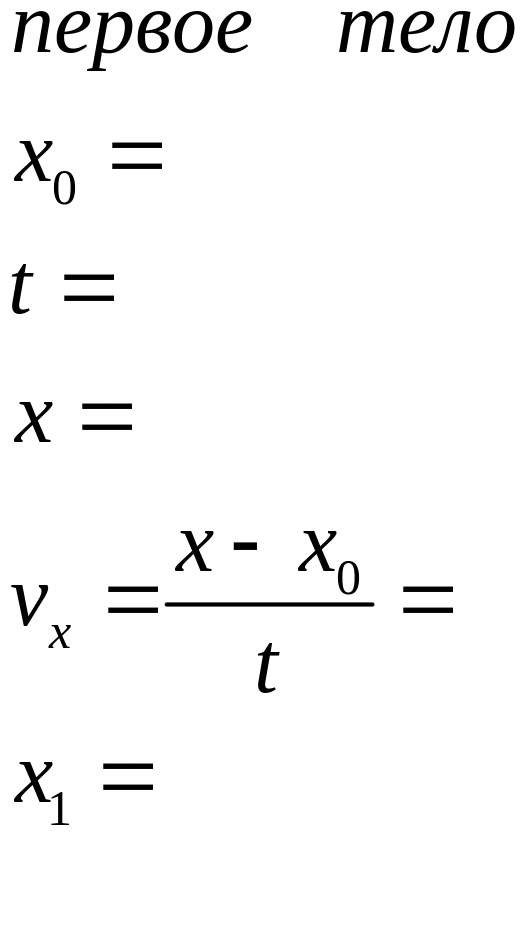 Прочитайте графики зависимости координаты тел от времени. Запишите уравнения движения для каждого тела. Следуйте предложенному порядку действий:

2 По графику зависимости координаты тела от времени постройте график зависимости проекции скорости тела от времени. Следуйте предложенному порядку действий.

3 По графику зависимости координаты тела от времени постройте график зависимости проекции скорости тела от времени. Следуйте порядку действий, предложенному в задании 2.

а)

б)

4 По графику зависимости проекции скорости от времени постройте график зависимости координаты тела от времени и опишите характер движения тела.

а )

б)