§ 3 Равномерное движение

Равномерное движение (РД) – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Равномерное движение в природе встречается не очень часто. Тем не менее, есть ситуации, в которых движения тел с хорошей точность можно считать равномерными. Например, маленький плотный шарик тонет в масле равномерно, при отсутствии ветра парашютист опускается равномерно, молекулы воздуха в разреженном газе двигаются равномерно между столкновениями…

Н аглядной демонстрацией РД является опыт с тележкой, на которой установлен сосуд с жидкостью. Капли жидкости отрываются от трубки через равные промежутки времени. Равные расстояния между упавшими на стол каплями свидетельствуют от равномерном движении тележки

Важно, что за любые равные интервалы времени совершаются равные перемещения.

Нетрудно видеть, что траекторией равномерного движения может быть только прямая линия.

Нам предстоит решить основную задачу механики для равномерного движения – определить зависимость координат тела от времени.

Для решения поставленной задачи вводем величину, характеризующую быстроту движения – скорость.

Скоростью равномерного движения называют отношение перемещения ко времени, за которое оно было совершено:

. (3.1)

Физический смысл скорости – это величина, численно равная перемещению тела в единицу времени.

Скорость – величина векторная. Направление вектора скорости совпадает с направлением перемещения . Поскольку между векторами и их проекциями одинаковые действия, проекции скорости находятся по формулам

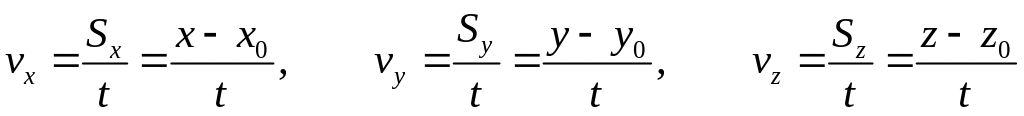. (3.2)

Модуль вектора скорости

. (3.3)

Единицы скорости в SI .

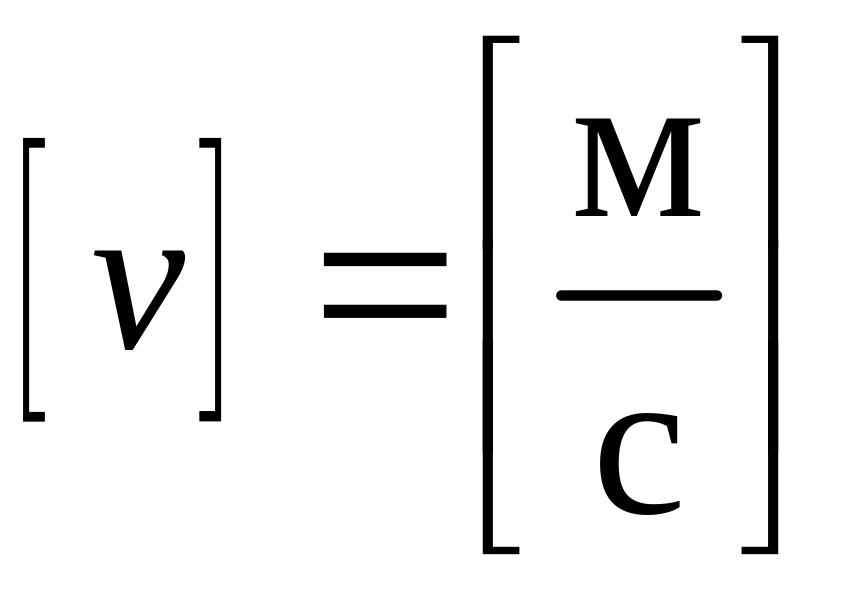Например, скорость звука в воде составляет 1400 м/с, а в воздухе 330 м/c – это значит, что за 1 с звуковая волна распространяется на расстояние 1400 м в воде и на 330 м в воздухе.

Из определения равномерного движения следует, что скорость равномерного движения постоянна – у нее неизменны направление и численное значение.

В таблице 1 приведены характерные значения модуля скорости различных тел в природе. Мы видим, что скорость леопарда достигает 30 м/с, а улитки всего лишь 0,0014 м/с. Это значит, что за 1 с леопард может переместиться на расстояние 30 м, а улитка на расстояние более чем в 10⁵ раз меньшее.

Таблица 1 - Скорости в живой природе

Кровь в капиллярах	0,0005 - 0,0020 м/с
Кровь в артериях	0,2 – 0,5 м/с
Нервный импульс	40 -100 м/с
Улитка	0,0014 м/с
Черепаха	0,05 – 1,3 м/с
Муха	1,7 м/с
Пешеход	1,3 - 1,8 м/с
Усейн Болт (рекорд)	12,2 м/с
Черный стриж	До 44 м/с
Леопард	До 30 м/с
Дельфин – касатка	До 15 м/с

В таблице 2 приведены значения модуля скорости различных транспортных средств. Видно, что скорость самолета 950 км/ч. Это значит, что за 1 ч самолет пролетает расстояние 950 км. Если мы уменьшим интервал времени, как в опыте с тележкой, то увидим, что за 1с самолет перемещается на 270 м.

Таблица 2 - Скорости в технике

Автобус ЛИАЗ	До 120 км/ч
Автомобиль Лада Гранта	До 167 км/ч
Мотоцикл Harley Davidson	235 км/ч Рекорд – 320 км/ч
Болид «Формулы – 1»	До 330 км/ч
Вертолет «Черная акула»	Крейсерская 270 км/ч На пикировании до 390 км/ч
Самолет Ту - 154	850 км/ч До 950 км/ч
Сверхзвуковой самолет	1,2 – 5 М, где М - скорость звука
Пуля из автомата Калашникова	715 м/с
Пассажирский поезд	До 90 км/ч
Поезд «Сапсан»	До 250 км/ч
Межконтинентальная ракета	До 16 000 км/ч
Спутник на низкой круговой орбите	8000 м/c
Космический аппарат	До 49 000 км/ч

Наконец, в таблице 3 мы видим скорости астрономических объектов и звуковых и световых волн. Заметьте, что скорость звука в воздухе 330 м/с, что примерно в 10⁶ раз меньше скорости света. Скорость света является максимальной скоростью, с которой могут двигаться тела в природе.

Таблица 3 - Скорости в природе

Орбитальная скорость Земли	30 км/с
Орбитальная скорость Луны	1 км/c
Солнце по отношению к центру галактики	250 км/с
Скорость звука в воздухе при 0 °С	330 м/с
Скорость молекул кислорода при 0 °С	425 м/c
Скорость молекул водорода при 0 °С	1700 м/c
Скорость ЭМВ в вакууме	300 000 км/c

Пользуясь определением скорости (3.1) и (3.2), можно получить зависимости координат тела от времени при равномерном движении

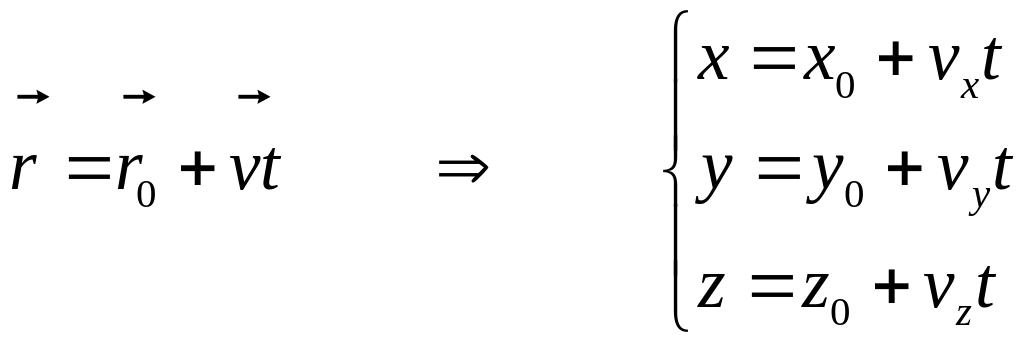. (3.4)

Проанализируем полученный результат.

При равномерном движении зависимость координаты тела от времени является линейной функцией. Например, заданы уравнения движения двух тел и (значения всех величин выражены в SI). Что можно узнать о характере движения тел по их уравнениям движения?

1 Оба тела двигаются вдоль оси ОХ, поскольку задана зависимость х(t).

2 Уравнения движения представляют собой линейные функции. Следовательно, оба тела двигаются равномерно, ибо только при равномерном движении зависимость координаты тела от времени является линейной функцией .

3 Сопоставим конкретные уравнения движения с общим видом уравнения равномерного движения.

Начальная координата первого тела .

Проекция скорости первого тела на ось ОХ . Проекция скорости отрицательна, следовательно, вектор скорости направлен противоположно оси ОХ.

Начальная координата второго тела .

Проекция скорости первого тела на ось ОХ . Проекция скорости положительна, следовательно, вектор скорости сонаправлен оси ОХ.

Видим, что тела двигаются навстречу друг другу. Возможно, так:

Примеры решения задач

Задача 1 Составление уравнения движения

Р асстояние между Токио и Осакой составляет 550 км. По скоростной железной дороге из Токио отправляется экспресс со скорость 220 км/ч. Через 6 минут после его отправления из Осаки в направлении Токио отправляется экспресс со скоростью 200 км/ч. Составьте уравнения движения экспрессов.

Решение

Сделаем схематичный рисунок, указав на нем положение станций отправления и направления движения поездов.

Введем систему отсчета. Достаточно одной координатной оси ОХ, параллельной железнодорожному пути, направим ее от Токио к Осаке. Пусть начало отсчета совпадает вокзалом в Токио. Тогда координата Осаки .

Момент начала движения экспресса из Токио примем за начало отсчета времени t.

Общий вид уравнения равномерного движения .

Начальная координата первого поезда .

Проекция скорости первого поезда (положительна, т.к. скорость сонаправлена оси ОХ).

Уравнение движения первого поезда км.

Начальная координата второго поезда .

Проекция скорости второго поезда (отрицательна, т.к. скорость направлена против оси ОХ).

Время движения второго поезда меньше времени движения первого на 6 мин = 0,1 ч, значит (ч).

Уравнение движения второго поезда (км).

Задача 2 Расстояние между автомобилями на трассе

Два автомобиля двигаются по прямолинейной трассе. Их уравнения движения выглядят следующим образом (время выражено в часах):

(км),

(км).

Каким будет расстояние между автомобилями в момент времени t = 30 мин.

Решение:

Расстояние между точками на числовой прямой находится как модуль разности их координат

(м).

Задача 3 Где будет экспресс?

С Савеловского вокзала с интервалом в 5 минут отправляются два экспресса. Уравнение движения первого экспресса (км). Где будет находиться второй экспресс по отношению к Савеловскому вокзалу, когда первый проследует станцию Новодачная? Время в уравнении движения выражено в часах.

Примечание: участок дороги от Савеловского вокзала до Новодачной можно считать прямолинейным. Новодачная находится в 15 км от Савеловского вокзала. Скорости экспрессов одинаковые.

Решение

В условии задачи по существу введена система отсчета. Делаем схематичный рисунок.

За начало отсчета времени принят момент отправления первого экспресса: если время движения первого экспресса ; время движения второго состава .

Второй состав, как и первый, движется равномерно. Его уравнение движения имеет вид .

Начальная координата второго экспресса , проекция скорости положительна и равна модулю, поскольку вектор скорости сонаправлен с осью ОХ . Уравнение движения второго экспресса принимает вид .

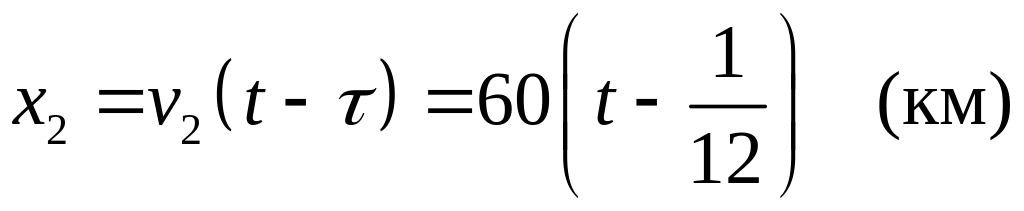Время движения первого экспресса до Новодачной находим из уравнения движения

,

ч.

Положение второго экспресса находим из уравнения его движения:

.

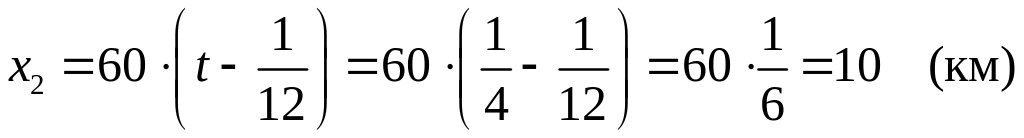Задача 4 Равномерное движение в плоскости

В о время хоккейного матча Малкин делает пас Овечкину. С хоккейной площадкой связана координатная плоскость ХОУ. Уравнения движения шайбы выглядят следующим образом:

Каковы координаты точки, в которой шайба испытала удар клюшкой? По какой траектории и в каком направлении двигается шайба? Чему равен модуль скорости шайбы? В какой точке площадки должна находиться клюшка Овечкина, чтобы он получил шайбу через 1 с?

Решение

Шаг 1 Начальные координаты шайбы определяем из уравнений движения

.

Шаг 2 Уравнение траектории связывает между собой координаты тела. Для нахождения уравнения траектории необходимо исключить время t из уравнений движения, заданных в условии.

.

Уравнение, связывающее координаты x и у, является линейной функцией, график которой – прямая. Таким образом, траектория точки – прямая.

Шаг 3 Оба уравнения движения представляют собой линейные функции. Следовательно, и вдоль оси ОХ, и вдоль оси ОУ шайба двигается равномерно, ибо только при равномерном движении зависимость координаты тела от времени является линейной функцией. Общий вид уравнений движения по осям ОХ и ОУ:

, .

Сопоставляя общий вид уравнений с конкретными уравнениями движения, находим проекции скорости на оси координат:

, .

Модуль скорости .

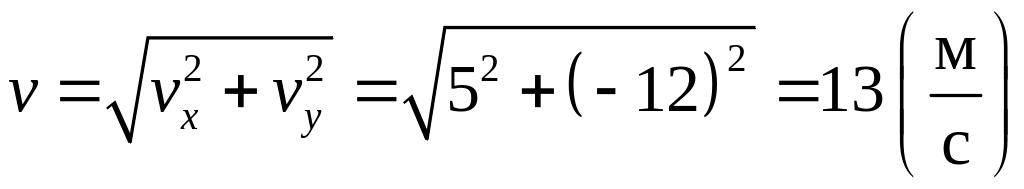Шаг 4 Направление движения определим из треугольника скоростей.

П роекция скорости на ось ОХ положительна, следовательно, составляющая скорости по оси ОХ сонаправлена с осью. Проекция скорости на ось ОУ отрицательна, следовательно, составляющая скорости по оси ОУ направлена против оси.

.

Н аправление вектора скорости задает угол θ между вектором и положительным направление оси ОХ:

Траектория точки показана на рисунке.

Координаты клюшки Овечкина находим из уравнений движения:

Задача 5 Встреча автомобиля и автобуса

Из Уфы в Стерлитамак отправляется рейсовый автобус со скоростью 70 км/ч. Через 20 минут навстречу ему из Стерлитамака выезжает фермер на автомобиле Ока. Скорость фермерского автомобиля 90 км/ч. Расстояние между Уфой и Стерлитамаком 130 км. Через какое время после выезда из Уфы водитель автобуса увидит пролетающую мимо него Оку? Где это произойдет? Считать движение равномерным.

Решение:

Шаг 1 Делаем схематический рисунок, изобразим на нем положение населенных пунктов и направления движения автобуса и автомобиля.

Шаг 2 Вводим систему отсчета:

а) достаточно одной оси координат, направленной вдоль дороги;

б) начало координат поместим в том пункте, откуда начинает двигать автобус;

в) время начнем отсчитывать в момент начала движения автобуса.

, .

Шаг 3 Составляет уравнения движения тел.

Шаг 4 При встрече координаты тел должны быть равными.

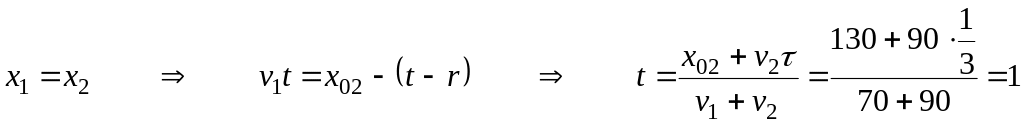
Шаг 5 Находим координату места встречи

.

Ответ: автобус встретит Оку через 1 час после выезда из Уфы на расстоянии 70 км от города.

Задачи для самостоятельного решения

1 Опишите движение тела и сделайте пояснительный рисунок. Все величины, входящие в уравнения движения, имеют размерность SI. Движение каких тел могли бы описывать эти уравнения?

• x = 20t – 1

• x = - 4t + 1

• x = 510t

• x = 100+0,001t

2 Два велосипедиста двигаются по шоссе. Уравнения их движения выглядят следующим образом

Определите расстояние между велосипедистами через минуту после начала движения. Координата и время в уравнениях движения выражены в единицах СИ.

3 Из пункта А в пункт В выехала автомашина с постоянной скоростью 80 км/ч. Спустя время =15 мин из пункта В в пункт А выехал велосипедист с постоянной скоростью 20 км/ч. Расстояние АВ = 55 км. Где и когда автомобиль и велосипедист встретятся?

4 Расстояние между станциями равно 18 км. От одной из них начинает равномерно двигаться товарный состав со скоростью 54 км/ч. Через час от второй станции в том же направлении выходит пассажирский состав, который тоже двигается равномерно со скоростью 72 км/ч. Где и когда пассажирский состав догонит товарный? Сколько решений имеет задача?

5 Расстояние между пристанями на озере равно 5 км. От одной из них начинает двигаться катер со скоростью 16 км/ч. Через 10 минут от второй пристани навстречу выходит другой катер, он движется со скоростью 12 км/ч. Где и когда катера встретятся?

6 Между Оренбургом и районным центром Сакмара проложена одноколейная железная дорога (в целях экономии). У дачного поселка Гребени дорога на небольшом участке «раздваивается», чтобы встречные поезда могли разойтись. Из Оренбурга отправляется пассажирский поезд со скоростью 52 км/ч. Одновременно из Сакмары в Оренбург отправляется электричка со скоростью 40 км/ч. Как долго должна простоять электричка в Гребенях, чтобы пропустить скорый поезд? Расстояние между Оренбургом и Сакмарой 42 км, Гребени удалены от Оренбурга на 26 км.

7 Электронный луч двигался по экрану. Зависимость координат х(t), y(t) луча от времени показана на рисунке. Какую фигурку вычертил луч на экране?