§ 12 Суперпозиция движений

Суперпозицией называется процесс наложения. О суперпозиции говорят в случае наложения электрических полей, созданных несколькими зарядами; в случае наложения магнитных полей, созданных несколькими токами; в случае наложения волн, бегущих от разных источников, и т.д.

Нас интересует явление наложения нескольких движений, в которых участвует тело. Одним из примеров суперпозиции движений является баллистическое движение. Тело, брошенное под углом к горизонту, одновременно участвует в двух независимых прямолинейных движениях: равномерном по горизонтали и равноускоренном по вертикали. Другой пример – планеты солнечной системы двигаются по окружности вокруг Солнца и вращаются вокруг собственной оси.

Идея заключается в следующем – разбивая сложное движение тела на несколько более простых независимых движений, мы облегчаем задачу описания движения тела. При таком подходе скорость любой точки тела является геометрической суммой скоростей в каждом движении

Рассмотрим случай наложения вращательного движения и поступательного, когда точка тела вращается, а ось вращения движется поступательно. Предлагаемая к рассмотрению задача может служить моделью следующих реальных ситуаций:

а ) катится колесо автомобиля, велосипеда, катится бильярдный шар, обруч и т.д.;

б) движется винт вертолета;

в) движется турбина двигателя самолета;

д) движение футбольного, волейбольного, теннисного мяча и т.д.

е) прыжок в несколько оборотов, совершаемый фигуристом, прыгуном в воду, гимнастом, акробатом.

Если для мячей и бильярдных шаров важно знать траектории и координаты тел, то для винтов, турбин важно знать скорости и ускорения точек тела – это позволит рассчитать нагрузки, испытываемые телом, а значит, правильно подобрать материал для них. От скорости вращения колес автомобиля зависит скорость его поступательного движения.

Пример 1 Качение колеса без проскальзывания

Пусть колесо радиусом R движется по плоской поверхности со скоростью и вращается с постоянной угловой скоростью . Запишите уравнения движения точек на ободе колеса, определите их скорости и ускорения. Какую траекторию описывают точки колеса?

Решение

Шаг 1 Систему отсчета свяжем с поверхностью, по которой катится колесо.

Оси координат расположим параллельно и перпендикулярно поверхности. За начало отсчета времени примем момент начала движения.

Шаг 2 Рассмотрим самую низкую точку на ободе колеса.

Из рисунка нетрудно видеть, что координаты точки А в момент времени t будут равны

где – угол поворота радиус-вектора точки А равен .

Тогда уравнения движения приобретают вид

На практике часто реализуется качение колеса без проскальзывания. Условие отсутствия проскальзывания – длина дуги , пройденная точкой А, равна пути , пройденному центром колеса:

При качении колеса без проскальзывания скорость поступательного движения равна скорости вращательного движения точек на ободе колеса. Колесо автомобиля приводится во вращение двигателем. Понятно, что скорость движения автомобиля прямо пропорциональна частоте вращения вала .

С учетом связи линейной скорости вращательного движения с угловой скоростью уравнения движения принимают вид

Уравнение траектории получается исключением из уравнений движения времени.

Рисунок 53 - Точка на ободе колеса описывает линию, называемую циклоидой

Точки, расположенные ближе к оси вращения и дальше от оси вращения двигаются соответственно по укороченной и удлиненной циклоиде:

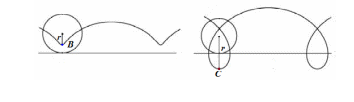
Рисунок 54 – Траектории движения различных точек катящегося колеса

Скорости точек вращающегося колеса можно рассчитать, дифференцируя уравнения движения

Для нахождения скорости точки можно рассуждать иначе. Мгновенная скорость любой точки колеса складывается из скорости вращательного движения (она у разных точек разная) и скорости поступательного движения (она для всех точек колеса одинаковая):

.

Рисунок 55 – Скорости точек на ободе катящегося колеса

Например, при движении колеса без проскальзывания скорости точек А, В и O’ равны

Скорости точек тела, совершающего сложное движение, можно определить, используя теорему Эйлера.

Любое движение твердого тела, имеющего одну неподвижную точку, можно рассматривать как вращение вокруг мгновенной оси, проходящей через эту неподвижную точку. С течением времени мгновенная ось, вообще говоря, непрерывно перемещается как в теле, так и в пространстве.

В случае качения колеса без проскальзывания неподвижной является точка касания колеса с поверхностью дороги. Этот факт дает право применить к колесу теорему Эйлера: два движения тела, поступательное и вращательное, можно заменить на одно, вращательное относительно оси, проходящей через точку O’.

Сравним угловые скорости вращения колеса относительно оси, проходящей через его центр, и относительно мгновенной оси вращения.

Для точек на ободе колеса угловая скорость вращения относительно оси, проходящей через центр:

.

Относительно мгновенной оси вращения, проходящей через точку O’, линейная скорость точки О равна , а ее расстояние до оси вращения равно R. Следовательно, угловая скорость вращения равна

.

Сравнивая результаты, видим, что угловая скорость относительно реальной оси, проходящей через центр колеса, и мгновенной оси вращения одинакова. Поэтому можно говорить об угловой скорости вращения твердого тела, не указывая, относительно какой оси это вращение происходит.

Пусть автомобиль движется со скоростью v₀. Используя теорему Эйлера, определим скорости точек А, В и С на ободе одного из колес автомобиля.

Шаг 1 Колеса автомобиля не проскальзывают. Следовательно, точка качания колеса с землей покоится относительно земли.

Ш аг 2 На основании теоремы Эйлера два движения колеса заменяем на одно - вращательное относительно точки . Скорости движения точек колеса относительно будут одновременно и скоростями точек относительно земли, ибо относительно земли покоится.

Шаг 3 Скорость центра колеса О относительно земли – это теперь скорость вращательного движения точки О относительно . Угловая скорость вращения относительно мгновенно оси

.

Такой же будет угловая скорость вращения всех точек колеса относительно оси, проходящей через .

Шаг 4 Точка В вращается относительно по окружности радиусом . Скорость точки В

.

Шаг 5 Точка А вращается относительно по окружности радиусом . Скорость точки А

.

Вектор скорости точки А должен быть перпендикулярен радиусу – отрезку А, следовательно вектор скорости направлен к точке В, ибо вписанный прямой угол опирается на диаметр окружности.

Шаг 6 Точка С двигается по окружности радиусом . Скорость точки С

.

Важно помнить, что применение теоремы Эйлера позволяет рассчитать только линейные скорости, но не позволяет найти ускорения различных точек тела.

Если колесо катится равномерно, то ускорение каждой точки колеса – это центростремительное ускорение за счет вращения вокруг оси колеса.

З адачи для самостоятельного решения

1 Шарик зажат двумя рейками, движущимися со скоростями м/с и м/с. Шарик не проскальзывает относительно реек. С какой скоростью и в каком направлении катится шарик?

2 Колесо, пробуксовывая, катится по ровной горизонтальной дороге. Найдите скорость поступательного движения колеса, если скорость верхней точки относительно земли составляет м/с, а скорость нижней точки м/с.