§ 10 Кинематические связи – передача движения

Под кинематическими связями понимают связь между перемещениями, скоростями и ускорениями различных точек тела или кинематическими величинами, характеризующими связанные тела.

Проблема чрезвычайно актуальна. Она связана с тем, что движение от одного тела необходимо передавать другому телу, вращательное движение нужно преобразовывать в поступательное или наоборот и т.д.

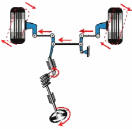
Движение от поршня ДВС передается на вал с колесами. От скорости движения поршня зависит скорость вращения колес и, в конечном итоге, самого автомобиля. С другой стороны, движение рулевого колеса должно приводить к повороту колес автомобиля.

Колеса велосипеда приводятся во вращательное движение педалями. Понятно, что скорость велосипеда зависит от того, как быстро велосипедист вращает педали.

Спортсмен на водных лыжах тросом соединен с катером. Скорость спортсмена связана с тем, как двигается катер.

Лодка на веслах. Нам важно знать, как связаны перемещение и скорость рук человека, сидящего на веслах, и перемещение и скорость самой лодки.

В любом станке движение от ротора электродвигателя передается на режущий, колющий инструмент, сверло, фрезу и т.д.

Тело человека – от величины сокращения и скорости сокращения мышцы зависит перемещение и скорость какой-либо части тела.

1 Движение можно передавать от одного тела другому, если каким-либо образом «зацепить» поверхности тел друг за друга. Это можно сделать при помощи:

а) зацепления зубчатых поверхностей

б) натянутого ремня;

в) натянутой цепи;

г) трения покоя между поверхностями.

Рассмотрите представленные фотографии. Пусть одно из тел в каждой связке приводится в движение. Как будет двигаться второе тело? В каком направлении будет происходить это движение?

Понятно, что линейные скорости точек в месте «зацепления» одинаковые .

2 Можно передавать движение от одного тела другому, расположив тела на одной оси вращения. В этом случае для всех точек всех тел одинаковой будет угловая скорость .

Цирковой велосипед. Колесо и педали насажены на одну ось, поэтому они вращаются с одинаковой угловой скоростью.

На тепловой электростанции на один вал насаживается более 20 турбин и ротор генератора. Водяной пар раскручивает систему до частоты 3000 об/мин.

2. Движение можно передавать, соединив тела при помощи стержня, троса.

Поршень в цилиндре движется поступательно, а связанный с поршнем шатун приводит вал во вращательное движение.

П арасейлинг и катание на банане – это примеры того, как движение передается от катера к телу при помощи троса.

Под действием внешних сил, действующих на стержень, связывающий тела, он деформируется. Однако, изменение длины твердого стержня под нагрузкой пренебрежимо мало в сравнении с его длиной в недеформированном состоянии.

Тросы под нагрузкой удлиняются. Но, чаще всего, это удлинение мало в сравнении с длиной нерастянутого троса.

В тех случаях, когда изменением линейных размеров тела можно пренебречь, используют модель абсолютно твердого тела. В этой модели линейные размеры тела считаются неизменными.

Допустим, стержень двигается так, как показано на рисунке.

Возможно ли такое движение стержня?

Разложим скорости концов стержня на две составляющие: параллельные стержню и перпендикулярные стержню .

За счет перпендикулярных составляющих скоростей стержень вращается (см. задание № 8 раздела «Кинематика вращательного движения»). За счет параллельных составляющих скоростей стержень должен двигаться поступательно вдоль направления АВ. Поскольку , расстояние АВ должно сокращаться, чего быть не может, ибо стержень абсолютно твердый.

Другая ситуация:

Ч то должно происходить со стержнем?

Разложив вектора скоростей точек А и В на перпендикулярную и параллельную составляющие, видим, что концы стержня А и В должны сближаться. Сближение точек А и В будет приводить к сжатию стержня, чего быть не может, ибо он абсолютно твердый.

Понятно, что возможно только такое движение абсолютно твердого стержня, при котором параллельные стержню (тангенциальные) составляющие скоростей всех его точек одинаковы . Этот вывод можно обобщить на движение абсолютно твердого тела любой формы: тангенциальные составляющие скоростей точек отрезка, соединяющего любые две точки тела, должны быть одинаковыми.

П римеры решения задач

Пример 1 Передача вращательного движения

Движение от шкива 1 передается шкиву 4 при помощи двух ленточных передач. С какой частотой вращается шкив 4, если шкив 1 вращается с частотой и радиусы всех шкивов известны.

Шаг 1 Шкивы 1 и 2 связаны ленточной передачей, следовательно, линейные скорости точек на ободах шкивов равны .

Шаг 2 Шкивы 2 и 3 находятся на одном валу, для них одинаковы угловые скорости .

Шаг 3 Шкивы 3 и 4 соединены ремнем, для точек на их поверхностях одинаковы линейные скорости .

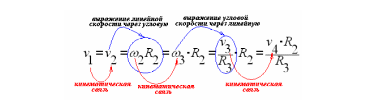
Шаг 4 Для перехода от первого шкива ко второму нужно по очереди выполнять две операции:

- записывать кинематическую связь;

- выражать линейную скорость через угловую или наоборот.

Шаг 5 Окончательно получаем .

Выражаем линейные скорости через частоту вращения и получаем ответ

.

Пример 2 Нахождение скорости конца стержня и скорости центра масс

Незакрепленный жесткий стержень АВ длиной 2 м движется так, что скорость конца А равна м/с и направлена под углом к стержню.

Чему равна скорость другого конца стержня, если известно, что она составляет угол со стержнем?

Ш аг 1 Разложим вектор скорости точки А на две составляющих – тангенциальную (параллельную) и нормальную (перпендикулярную) стержню

Шаг 2 Стержень жесткий, это значит что тангенциальные скорости всех точек стержня, направленные вдоль стержня, должны быть одинаковыми

Шаг 3 Опускаем перпендикуляр из конца тангенциальной составляющей скорости точки В на линию, вдоль которой располагается стержень, и находим вектор скорости точки В. Достраиваем нормальную составляющую скорости точки В.

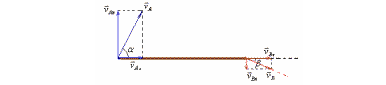
Шаг 4 Скорость точки В

м/с.

Ш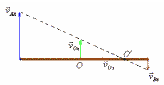 аг 5 За счет тангенциальной составляющей скорости стержень двигается вправо со скоростью .

Шаг 6 За счет нормальных составляющий скоростей стержень вращается. Найдем построением мгновенную ось вращения и скорость центра масс (она находится посередине, если стержень однородный.

Шаг 7 Нормальная скорость центра масс стержня, точки О, равна

м/с.

Ш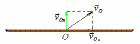 аг 8 Полная скорость центра масс стержня - точки О.

м/с.

Пример 3 Кривошипно-шатунный механизм

В двигателе Ваз-21083 длина шатуна равна 121 мм, диаметр вала – 82 мм. Чему равна скорость поршня в тот момент, когда шатун перпендикулярен радиусу вала? На первой передаче двигатель делает 2400 об/мин.

Решение:

Шаг 1 Рассмотрим устройство ДВС. Модель кривошипно-шатунного механизма представлена рядом. Отрезок ОА – радиус вала, АВ – шатун, связывает поршень с коленчатым валом.

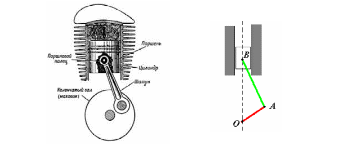
Шаг 2 Точка А двигается по окружности радиусом ОА, следовательно, вектор скорости точки А всегда перпендикулярен отрезку ОА. В момент, о котором говорится в задаче, скорость точки А проходит вдоль шатуна АВ.

Шаг 3 Запишем условие того, что шатун – жесткий стержень

.

Шаг 4 Выразим линейную скорость точки А через частоту вращения вала, а косинус угла найдем, зная геометрические размеры кривошипно-шатунного механизма.

.

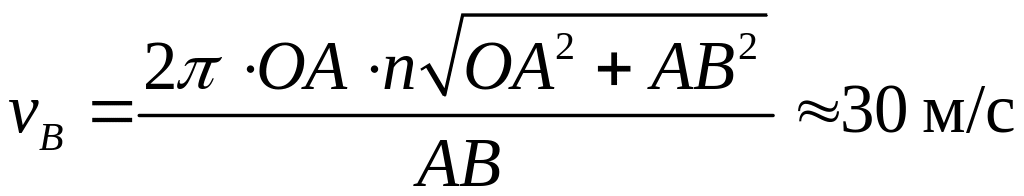Контрольные вопросы

1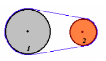 Большое колесо 1 приводится во вращательное движение ногами швеи и передается на маховик швейной машины 2 при помощи натянутого ремня. Составьте правильное утверждение.

Направление вращения колеса и маховика (одинаковое, противоположное). Для точек на ободе каждой колеса и маховика одинаковы (угол поворота, линейные скорости, угловые скорости, нормальные ускорения, тангенциальные ускорения, угловые ускорения).

2 Грузы 1 и 2 подвешены на нерастяжимых тросах к дифференциальному блоку. Радиусы шкивов, на которые наматываются тросы, отличаются в два раза. В некоторый момент времени скорость и ускорение первого груза оказались равными . Найдите скорость и ускорение второго груза в этот момент времени.

А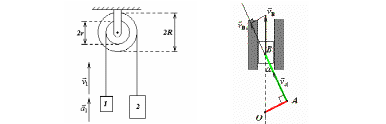 ) м/с; ; Б) м/с; ;

В) м/с; ;

3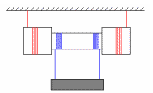 Груз опускается относительно земли со скорость 0,3 м/с. Радиус внутреннего цилиндра , радиус внешнего цилиндра R =1 cм. Какова скорость оси катушки относительно земли?

А) 0,5 м/с; Б) 0,75 м/с; В) 2 м/с.

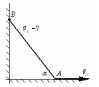
4 Стержень, поставленный в угол, скользит, не отрываясь от пола и стенки. В некоторый момент времени скорость точки А оказалась равной . Чему равна скорость точки В, если стержень составляет с полом угол ?

А) 15 см/с; Б) 17,3 см/с; В) 26 см/с; Г) 63 см/с.

5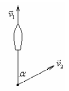 Катер, двигаясь со скоростью , тянет за собой спортсмена на водных лыжах. Лыжи составляют с тросом угол . С какой скоростью двигается спортсмен на водных лыжах?

А) 10 км/ч; Б) 34 км/ч; В) 17 км/ч; Г) 40 км/ч.

Задачи для самостоятельного решения

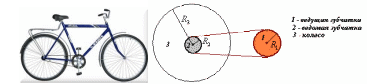
1 Диаметр колеса велосипеда «Пенза» равен 70 см, ведущая зубчатка имеет 48 зубьев, а ведомая – 18 зубьев. С какой скоростью движется велосипедист на этом велосипеде при частоте вращения педалей 1 об/с?

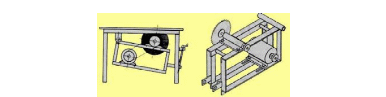
2 Циркулярная пила имеет диаметр 600 мм. На ось пилы насажен шкив диаметром 300 мм, который приводится во вращение посредством ременной передачи от шкива диаметром 120 мм, насаженного на вал электродвигателя. Какова скорость зубьев пилы, если вал электродвигателя совершает 1200 об/мин?

3 За трос тянут со скоростью v = 1 м/с. Что происходит с грузом?

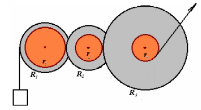
см, см;

см, см;

см, см;

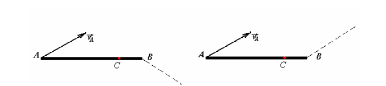
4 На рисунке показана скорость одного из концов стержня АВ. Пунктирной линией показано направление скорости точки В. Построением найдите скорость точки В. Каков характер движения стержня? Постройте вектор скорости точки С.

5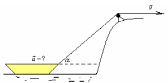 Лодку подтягивают к берегу, выбирая трос с постоянной скоростью . Какой будет скорость лодки u, когда трос будет составлять с поверхностью воды угол ?

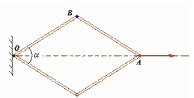
6 Шарнирная конструкция представляет собою ромб. Определите скорость точки В в тот момент, когда точка А двигалась со скоростью и угол был равен .