§ 9 Кинематика вращательного движения

Отличительная особенность вращательного движения – повторяемость. Факт повторяемости движения находит отражение в таких величинах как период и частота.

Периодом Т называется время совершения одного полного оборота. Единицы измерения периода в SI - секунда .

Частота n – число оборотов, совершаемых в единицу времени. Единицы измерения частоты в SI - .

Очевидно, что период и частота являются взаимно обратными величинами .

Кинематические характеристики вращательного движения разделяют на два класса – линейные и угловые.

1 Для определения местоположения точки на окружности используют понятие длины дуги l – это длина траектории или пройденный точкой путь.

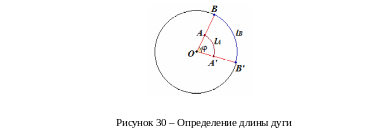
Допустим, точки А и В находятся на одной спице велосипедного колеса. При повороте спицы точка А переходит в положение , точка В переходит в положение B’. Видим, что за одно и то же время пути, проходимые разными точками вращающегося тела, разные. Это создает неудобство при описании вращательного движения: например, сообщая, что длина дуги равна l = 1,5 м, нужно уточнить, о какой точке идет речь.

Желательно ввести такую величину, характеризующую вращение, которая была бы одинаковой для всех точек тела. Из рисунка видно, что угол , на который повернулись радиус-векторы точек А и В, одинаков. Этот угол называют углом поворота радиус-вектора или просто углом поворота. Единицей измерения угла поворота является радиан .

Длина дуги связана с углом поворота

. ( 9.1)

Большие пути проходят те точки вращающего тела, которые расположены дальше от оси вращения.

2 Для характеристики быстроты движения вводят скорости.

Линейная скорость – уже известная мгновенная скорость. Мгновенная скорость всегда направлена по касательной к траектории. Следовательно, линейные скорости точек вращающегося тела направлены по касательной к окружности.

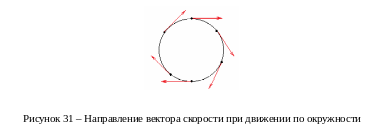
Модуль мгновенной скорости – величина, численно равная длине дуги (пройденному пути), пройденной в единицу времени.

Частным случаем движения по окружности является движение с постоянной по модулю скоростью . Такое движение нельзя назвать равномерным. При РД неизменным должен быть вектор скорости : сохраняться должны модуль и направление скорости. При движении по окружности направление скорости непрерывно изменяется. Однако, вращение с постоянной по модулю скоростью можно рассматривать как аналог РД. В этом случае нет необходимости находить мгновенную скорость как производную:

. (9.2)

За время, равное периоду, точка совершает один оборот, т.е. проходит путь, равный длине окружности

. (9.3)

Видим, что модуль линейной скорости прямо пропорционален радиусу. Во сколько раз отличаются радиусы точек, во столько же раз отличаются их скорости. Этот факт позволяет изображать графически скорости разных точек вращающегося тела.

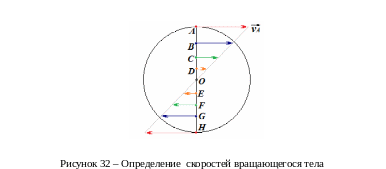
Для описания вращательного движения тела пользоваться линейной скоростью неудобно, поскольку линейные скорости разных точек разные. В связи с этим вводят понятие угловой скорости .

. ( 9.4)

Угловая скорость – это производная от угла поворота по времени. Физический смысл угловой скорости - это величина, численно равная углу поворота в единицу времени. Угловая скорость одинакова для всех точек вращающегося тела.

Единицы измерения угловой скорости в SI .

Угловой скорости приписывают направление. Необходимость этого поясняет пример: для автомобиля не безразлично, в каком направлении вращаются его колеса.

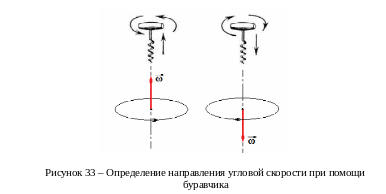
Вектор угловой скорости располагается вдоль оси вращения. Для определения направления вектора пользуются правилом буравчика: если поворачивать рукоятку буравчика по направлению вращения тела, то поступательное движение буравчика укажет направление вектора .

Буравчик или правый винт можно заменить правой рукой: загибаем четыре пальца правой руки по направлению вращения, отогнутый большой палец указывает направление угловой скорости.

Вращение с постоянной угловой скоростью является аналогом РД. В этом случае для нахождения модуля угловой скорости не нужно использовать правила дифференцирования. Скорость находят как при РД:

.

За время, равное периоду , тело поворачивается на угол радиан:

. ( 9.5)

Сравнивая выражения (9.3) и (9.5) , видим, что модули линейной и угловой скоростей связаны друг с другом:

. (9.6)

3 Вращательное может происходить с постоянной по модулю скорость, может разгоняться или тормозиться. Для характеристики быстроты изменения скорости вводят ускорения.

Даже если модуль линейной скорости точки остается неизменным, вектор скорости изменяется, поскольку изменяется направление скорости. Это означает, что движение по окружности всегда ускоренное.

Линейное ускорение - это производная от линейной скорости по времени. Выясним, как направлено линейное ускорение и каков его модуль.

Направление вектора ускорения совпадает с направлением вектора изменения скорости . Модуль ускорения равен производной от модуля скорости .

а) Рассмотрим движение по окружности с постоянной по модулю скоростью.

За малый промежуток времени материальная точка переместилась из положения А в положение В. Радиус-вектор точки повернулся на угол dφ.

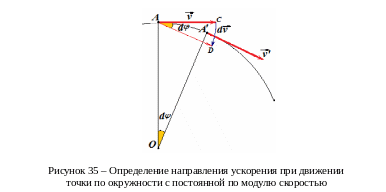
Поскольку вектор скорости перпендикулярен радиус-вектору, он тоже повернулся на угол dφ.

Для построения вектора изменения скорости параллельным переносом перемещаем вектор в точку А.

.

Треугольник ACD равнобедренный, так как его стороны – вектора скорости, а модуль скорости не изменялся.

В равнобедренном треугольнике углы при основании равны

.

За малое время угол поворота . Это значит, что углы при основании в равны . Таким образом, вектор изменения скорости перпендикулярен скорости , т.е. направлен вдоль радиуса к центру окружности. Вектор ускорения , сонаправленный изменению скорости , направлен вдоль радиуса к центру окружности. По этой причине ускорение называют центростремительным или нормальным (перпендикулярным скорости), обозначают или .

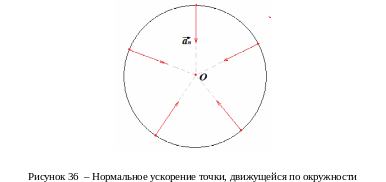
Рассчитаем модуль нормального ускорения. Треугольники ACD и OAA’ подобны. В подобных треугольниках соответственные стороны пропорциональны

.

Изменение скорости равно

.

Находим модуль ускорения

.

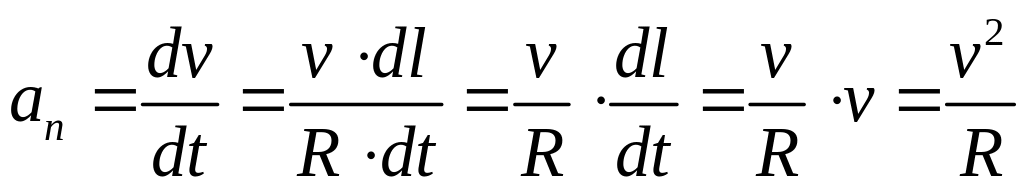. ( 9.7)

б) Изменяется модуль скорости

Переносим вектор в точку А и находим изменение скорости .

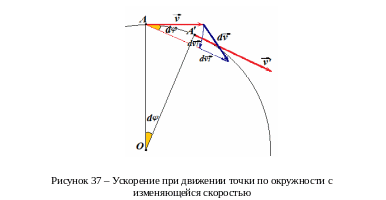
Проводим из точки А дугу радиусом v. В этом случае изменение скорости можно представить как сумму векторов

.

Ускорение разбивается на две части

.

Первое слагаемое – уже известное нормальное ускорение, обеспечивающее изменение направления скорости.

Величина - изменение модуля скорости. Поэтому второе слагаемое обеспечивает изменение численного значения скорости. Его называют тангенциальным или касательным ускорением. Это ускорение параллельно вектору скорости ║ .

Подведем итог. В общем случае ускорение материальной точки, движущейся по окружности, складывается из двух частей – нормального и тангенциального ускорений. Первое изменяет направление вектора скорости, второе – его модуль.

. (9.8)

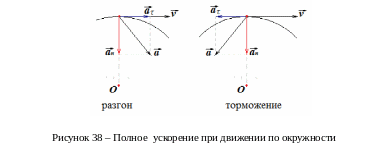
Очевидно, в случае разгона тангенциальное ускорение сонаправлено со скоростью , в случае торможения – направлено против скорости .

Модуль полного ускорения находится по теореме Пифагора

. (9.10)

Частный случай – вращение с постоянным по модулю тангенциальным ускорением . Очевидно, что такое движение является аналогом РУД, и на него можно перенести все соотношения, полученные для РУД:

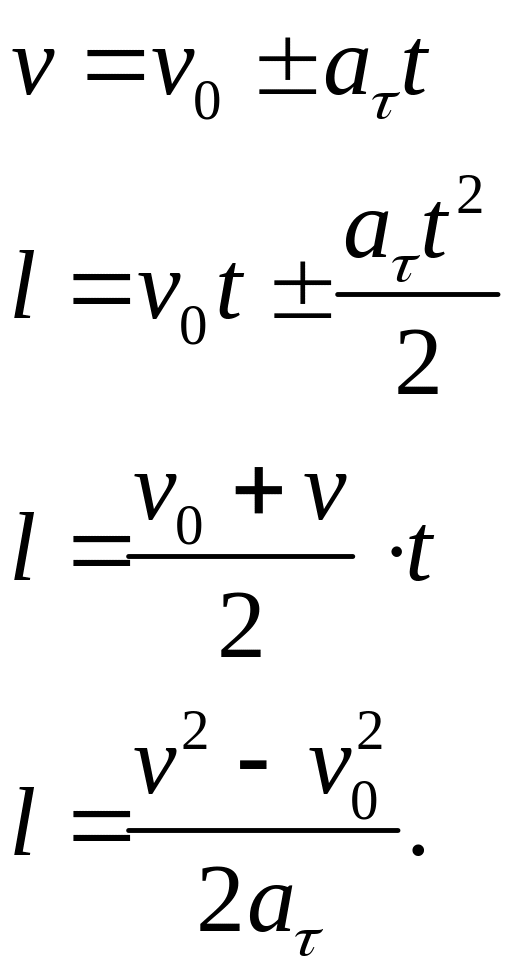
Знак «+» используется в формулах для случая разгона, знак «-» для торможения.

Линейное ускорение для разных точек вращающегося тела разное. Для описания вращательного движения удобнее пользоваться величинами, которые для всех точек одинаковы.

Угловое ускорение - это производная от угловой скорости по времени. Физический смысл углового ускорения – это величина, численно равная изменению угловой скорости в единицу времени.

Единица измерения углового ускорения в SI . Допустим, угловое ускорение равно - это значит, что угловая скорость изменяется на за секунду.

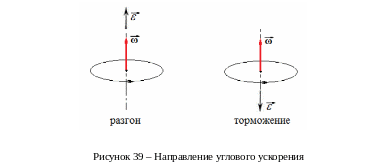
Если угловое ускорение постоянно , для угловых кинематических характеристик движения можно по аналогии переписать все формулы РУД:

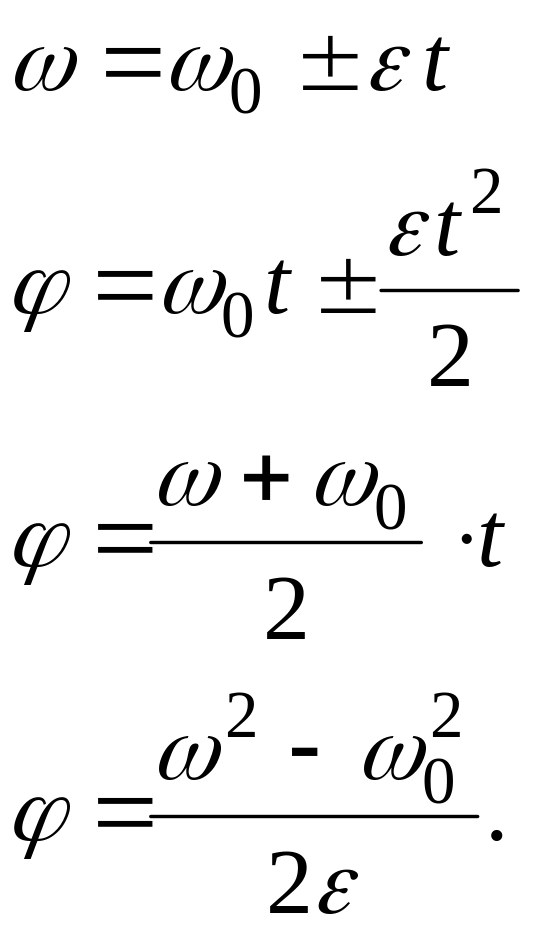
Знак «+» используется в формулах для случая разгона, знак «-» для торможения.

Угловое ускорение связано с тангенциальным ускорением:

.

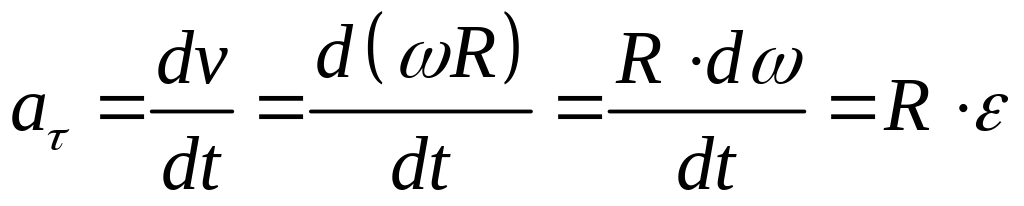. (9.11)

Примеры решения задач

Пример 1 Скорости точек велосипедного колеса

С какой частотой вращается велосипедное колесо, если линейная скорость точек на ободе равна v₁ = 3,6 м/с, а скорость точек, расположенных на 10 см ближе к оси v₂ = 2 м/с?

Шаг 1 Для всех точек вращающегося твердого тела частота вращения одинакова .

Шаг 2 Выразим линейные скорости точек через частоту и радиус окружности

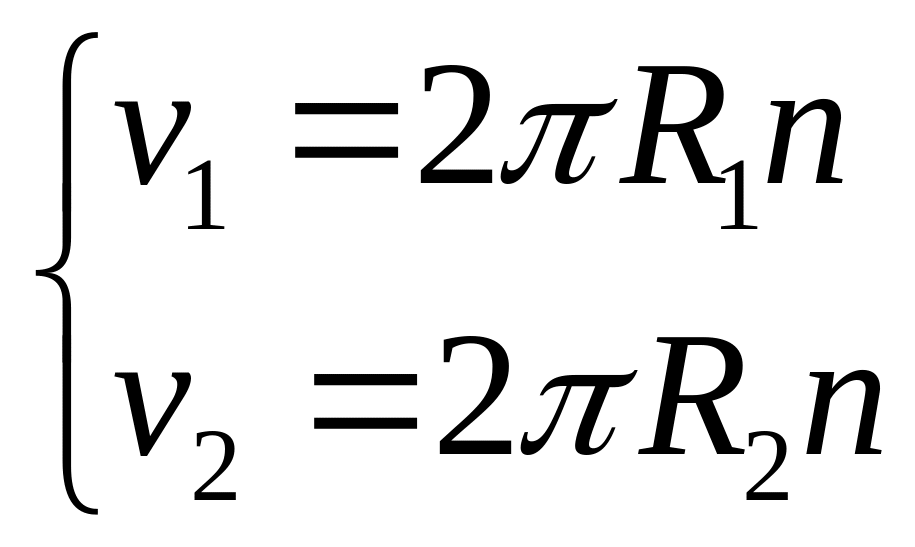
Шаг 3 Вычтем из одного уравнения другое и найдем частоту вращения n:

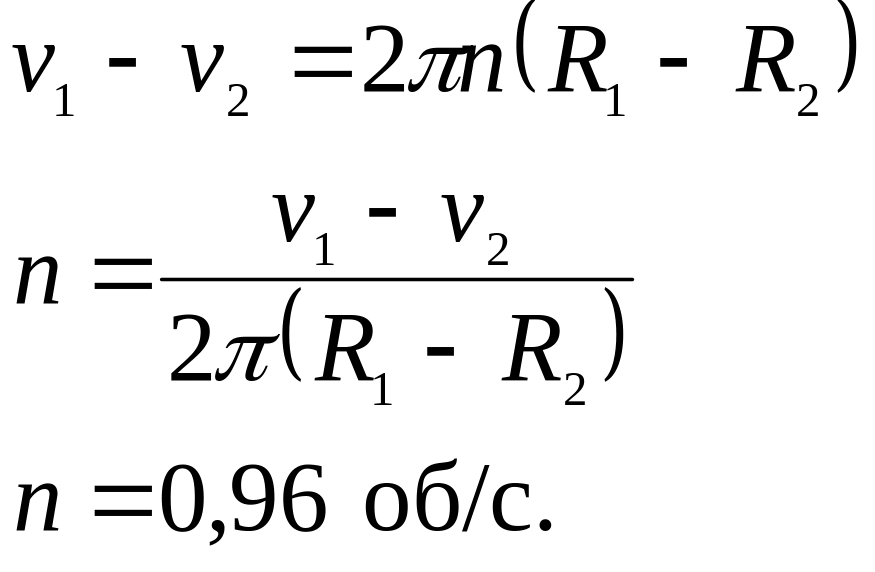
П ример 2 Самолеты выполняют вираж

Самолеты пилотажной группы «Витязи» выполняют разворот в горизонтальной плоскости, двигаясь на одинаковых расстояниях друг от друга по траекториям, которые показаны на рисунке. Ближайший к центру виража самолет движется по окружности радиуса 500 м, средний самолет движется со скоростью 396 км/ч, центростремительное ускорение третьего самолета 24 м/с². Чему равно расстояние между самолетами?

Шаг 1 Угловые скорости вращения самолетов одинаковые, так как радиус-вектор каждого из них за одинаковое время повернулся на одинаковую величину.

Шаг 2 Выразим линейную скорость второго самолета и ускорение третьего через угловую скорость

Шаг 3 Исключаем из системы угловую скорость и находим расстояние между самолетами

.

.

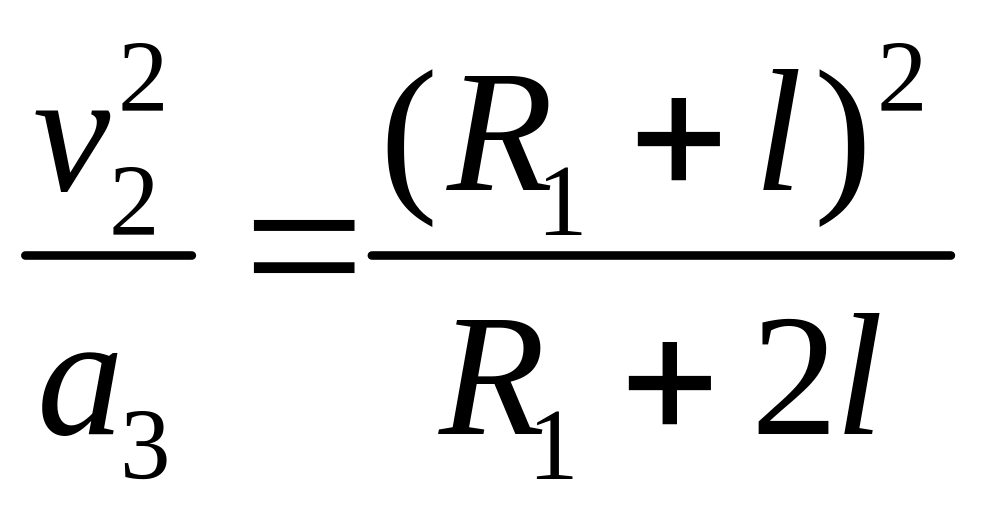Пример 3 Замедленное вращение колеса

Колесо, вращаясь с постоянным угловым ускорением, при торможении уменьшило свою угловую скорость за 1 мин от 5 рад/с до 2 рад/с. Найдите угловое ускорение колеса и число оборотов, совершенных за это время.

Решение:

Шаг 1 Движение колеса – аналог РУД, так как угловое ускорение колеса неизменно. Для описания такого движения можно пользоваться всеми формулами для РУД.

Шаг 2 Угловая скорость меняется по закону (знак «-», так как колесо тормозит). Тогда угловое ускорение ,

Шаг 3 Угол поворота .

Шаг 4 Число оборотов, совершенных турбиной равно ,

об.

Пример 4 Раскручивание колеса турбины

Колесо турбины раскручивают из состояния покоя с постоянным угловым ускорением . Чему равно полное ускорение точки, находящейся на расстоянии от оси вращения, через 5 с после начала движения? Сколько оборотов сделает турбина к этому моменту времени?

Решение:

Шаг 1 Колесо раскручивается с постоянным угловым ускорением, следовательно, его движение является аналогом РУД. Можно пользовать всеми формулами для равноускоренного движения.

Шаг 2 Угловая скорость турбины при разгоне меняется по закону . Поскольку турбина приходит в движение из состояния покоя, то .

Шаг 3 Полное ускорение точек на ободе турбины ,

где тангенциальное ускорение ,

нормальное ускорение .

Подстановка дает полное ускорение точек на ободе

Шаг 4 Угол поворота . Тогда число оборотов, совершенных турбиной равно

, об.

Пример 5 Радиус кривизны траектории

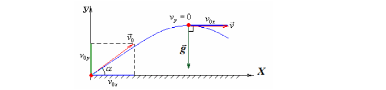
Волейбольный мяч брошен со скоростью 16 м/с под углом 60⁰ к горизонту. Определите радиус кривизны траектории в точке наивысшего подъема мяча.

Решение:

Шаг 1 Траекторией движения мяча является парабола. Однако малый элемент любой кривой линии можно аппроксимировать (примерно считать) элементом окружности. Таким образом, нахождение радиуса кривизны параболы в ее вершине сводится к нахождению радиуса окружности, «кусочек» которой сливается с параболой в вершине.

Шаг 2 В верхней точке траектории вертикальная составляющая скорости мяча становится равной нулю, вектор скорости направлен горизонтально и численно равен горизонтальной составляющей скорости с момент броска .

Шаг 3 Ускорение в любой точке траектории – это ускорение свободного падения , оно направлено вертикально вниз. В верхней точке параболы это ускорение перпендикулярно скорости, следовательно, тангенциальное ускорение в этой точке отсутствует, полное ускорение совпадает с нормальным ускорением .

Шаг 4 Нормальное ускорение рассчитывается через скорость и радиус кривизны траектории

.

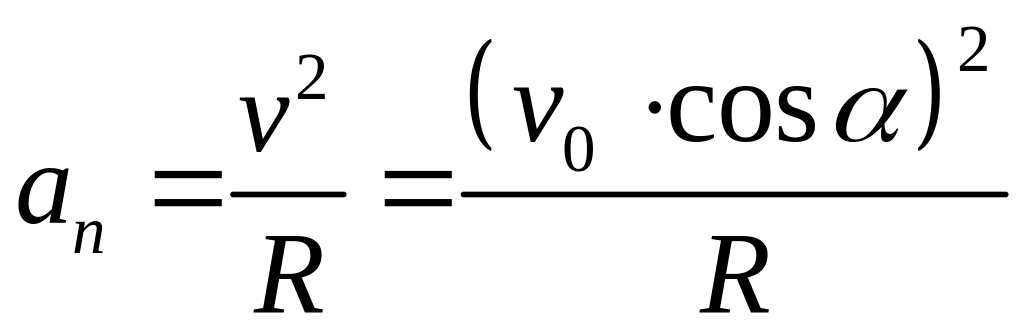Находим радиус кривизны траектории

.

.

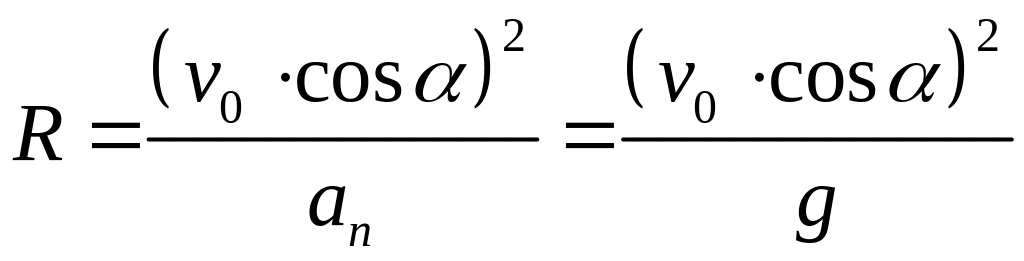Контрольные вопросы

1 Определите угол поворота минутной стрелки за указанные промежутки времени

Время	10 мин	15 мин	0,5 часа	1 час	3 часа
Угол поворота, рад

2 Составьте правильные утверждения (подчеркивая нужную фразу в скобках)

Период (n, T, v) – это физическая величина, численно равная (времени, перемещению, углу поворота, числу оборотов)(за определенное время, за один оборот, за единицу времени, совершения одного полного оборота). Основная единица измерения периода – (радиан, рад/с, об/с, секунда, м/с). Период всех точек вращающегося тела (одинаковый, разный).

Частота (n, T, v) – это физическая величина, численно равная (времени, перемещению, углу поворота, числу оборотов)(за определенное время, за один оборот, за единицу времени, совершения одного полного оборота). Основная единица измерения частоты – (радиан, рад/с, об/с, секунда, м/с). Частота всех точек вращающегося тела (одинаковая, разная).

Период и частота связаны соотношением ( , , )

3 Составьте правильные утверждения (подчеркивая нужную фразу в скобках)

Линейная скорость (n, T, v, φ, ω) – это физическая величина, численно равная ( углу поворота, числу оборотов, длине дуги), пройденн(-ой, -ому) вращающейся точкой за (один оборот, определенный промежуток времени, за единицу времени). Основная единица измерения линейной скорости – (радиан, рад/с, об/с, секунда, м/с). Линейная скорость всегда направлена (к центру окружности, по часовой стрелке, по касательной к окружности, против часовой стрелки). Линейная скорость разных точек вращающегося тела (разная, одинаковая)

4 Составьте правильные утверждения (подчеркивая нужную фразу в скобках)

Угловая скорость (n, T, v, φ, ω) – это физическая величина, численно равная ( углу поворота, числу оборотов, длине дуги), пройденн(-ой, -ому) вращающейся точкой за (один оборот, определенный промежуток времени, за единицу времени). Основная единица измерения линейной скорости – (радиан, рад/с, об/с, секунда, м/с). Угловая скорость разных точек вращающегося тела (разная, одинаковая).

5 Выберите правильное утверждение

А) Если линейная скорость с течением времени не изменяется, то вращательное движение в этом случае можно назвать равномерным;

Б) Линейная скорость вращательного движения постоянно изменяется по направлению. Поэтому вращательное движение никогда не бывает равномерным, даже если численное значение линейно скорости остается неизменным с течением времени

6 Материальная точка совершает вращательное движение с постоянной по модулю скоростью. Период вращения Т. Установите соответствие между физическими величинами и формулами для их расчета.

Физическая величина	Расчетная формула
Время движения
Число оборотов
Линейная скорость
Угловая скорость

7. Материальная точка совершает вращательное движение с постоянной по модулю скоростью. Частота вращения n. Установите соответствие между физическими величинами и формулами для их расчета.

Физическая величина	Расчетная формула
Время движения
Число оборотов
Линейная скорость
Угловая скорость

8 Выберите из ниже перечисленных формул те, которые позволяют рассчитать центростремительное (нормальное) ускорение.

А) ; Б) ; В) ; Г) ; Д) ; Е) .

9 Сравните линейные и угловые скорости точек А и В, расположенных на вращающемся колесе турбины.

А) ;

Б) ;

В) ;

Г) .

1 0 Сравните центростремительные ускорения точек А и В, расположенных на вращающемся колесе турбины.

А) ;

Б) ;

В) ;

Г) .

1 1 Тело движется равномерно по окружности в направлении против часовой стрелки. Как направлен вектор ускорения при таком движении?

А) 1; Б) 2; В) 3; Г) 4.

1 2 Тело разгоняется по окружности в направлении против часовой стрелки. Как направлен вектор полного ускорения при таком движении?

А) 1; Б) 2; В) 3; Г) 4; Д) 5; Е) 6.

1 3 Тело тормозит, двигаясь по окружности в направлении по часовой стрелке. Как направлен вектор полного ускорения при таком движении?

А) 1; Б) 2; В) 3; Г) 4; Д) 5; Е) 6.

14 Автомобиль движется по закруглению дороги радиусом 20 м с центростремительным ускорением 5 м/с². Скорость автомобиля равна

А) 12,5 м/c; Б) 10 м/c; В) 5 м/c; Г) 4 м/c.

15 Точка движется по окружности радиуса R со скоростью . Как изменится центростремительное ускорение точки, если ее скорость уменьшить в два раза, а радиус окружности в два раза увеличить?

А) Уменьшится в 2 раза; Б) Увеличится в 2 раза;

В) Уменьшится в 8 раз; Г) Увеличится в 8 раз.

16 Как известно, ускорение – это физическая величина, характеризующая быстроту изменения скорости. В связи с этим составьте правильные утверждения.

А) Тангенциальное ускорение изменяет линейную скорость …

Б) Нормальное ускорение изменяет линейную скорость …

1) …по направлению;

2) …по модулю.

Задания для самостоятельного решения

1 Рассчитайте линейную скорость точек земного экватора и точек, расположенных на широте . Как зависит линейная скорость точек земной поверхности от широты местности?

2 Чему равна линейная скорость точек на ободе паровой турбины тепловой электростанции, если ее диаметр равен 2,4 м и вращается она с частотой 3000 об/мин.

3 Найдите линейную скорость Луны, обусловленную ее обращением вокруг Земли. Период вращения Луны равен 27,3 суток. Расстояние от Земли до Луны составляет 3,84·10⁵ км.

4 Равномерно движущаяся по окружности точка делает полный оборот за 5 с. Чему равна угловая скорость точки? Чему равен угол поворота точки за 2 с?

5 Скорость точек рабочей поверхности шлифовального круга не может превышать 100 м/с. Найдите предельную частоту вращения круга, диаметр которого 40 см. Определите нормальное ускорение точек рабочей поверхности.

6 Рассчитайте центростремительное ускорение точек земного экватора и точек, расположенных на широте . Как зависит центростремительное ускорение точек земной поверхности от широты местности?

7 Найдите радиус вращающегося колеса, если линейная скорость точек на ободе в 3 раза больше скорости точек, находящихся на расстоянии 12 см ближе к оси.

8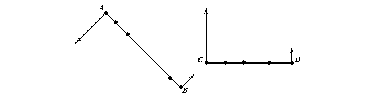 Могут ли скорости концов стержня быть направлены так, как показано на рисунке? Каков характер движения стержня? Изобразите скорости трех предложенных точек стержня.

9 На экране демонстрируется движущаяся повозка. Радиус колес повозки 35 см, они имеют по 16 спиц. Съемочная группа перемещает пленку со скоростью 24 кадра в секунду. Считая, что колеса повозки катятся без проскальзывания, определите, с какой скоростью должна двигаться повозка, чтобы колеса на экране казались неподвижными.

10 Материальная точка движется по окружности радиуса R = 10 см. пройденный путь зависит от времени по закону , где А = 1 м/с. Найдите линейную и угловую скорости, ускорение точки и число оборотов, сделанных за первые 5 с движения.

11 Волейбольный мяч брошен со скоростью 16 м/с под углом 60⁰ к горизонту. Найдите радиус кривизны траектории мяча в точке броска.

12 Вал вращается с постоянной частотой 180 об/мин. С некоторого момента вал тормозится с постоянным угловым ускорением, численно равным 3 рад/с². Через сколько времени вал остановится? Сколько оборотов он сделает до полной остановки?

13 Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением. Найдите нормальное и полное ускорение точки через 20 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки была равна 10 см/c.

14 Вал вращается с постоянной частотой 180 об/мин. С некоторого момента вал тормозится с постоянным угловым ускорением, численно равным 3 рад/с². Через сколько времени вал остановится? Сколько оборотов он сделает до полной остановки?

15 Точка движется по окружности с постоянным угловым ускорением ε = 1 рад/с². Найдите угол между скоростью и ускорением через 1 с после начала движения. Начальная скорость точки .

16 Шкив радиусом R = 0,5 м приводится во вращение с помощью веревки, намотанной на него. Конец веревки тянут с ускорением . Найдите нормальное, тангенциальное и полное ускорение точек на ободе шкива через 2 с после начала движения.

17 Угол поворота диска радиусом R = 10 см изменяется с течением времени по закону . Определите зависимость угловой скорости диска от времени. Чему равно полное ускорение точек на ободе диска через один оборот после начала движения.