§8 Баллистическое движение

Рассмотрим движение тела, брошенного под углом к горизонту. Такое движение можно представить как результат наложения двух независимых движений – равномерного по горизонтали и равноускоренного с ускорением свободного падения по вертикали.

Выясним особенности такого движения на примере движения снаряда, выпущенного из орудия под углом к горизонту. Мы определим следующие характеристики снаряда: скорость и координаты снаряда как функции времени, максимальную высоту подъема и дальность полета.

Пример 1 Скорость тела, брошенного под углом к горизонту.

Снаряд выпущен из орудия под углом α = 30⁰ к горизонту. Начальная скорость снаряда 200 м/с. Рассчитайте скорость снаряда через 5 с и 15 с после начала движения. Как направлена скорость в эти моменты времени? В какой точке траектории снаряд будет обладать минимальной скоростью, и чему она равна?

Р ешение:

1 Вводим систему отсчета. Оси системы координат направляем горизонтально и вертикально вверх. Начало координат помещаем в точку, из которой снаряд пришел в движение. Начало отсчета времени – момент начала движения.

2 Определим характер движения тела.

Сила тяжести сообщает снаряду ускорение . Проекции ускорения на координатные оси:

по горизонтали снаряд движет равномерно со скоростью ;

по вертикали снаряд движется равноускоренно, .

3 По вертикали скорость тела меняется по закону .

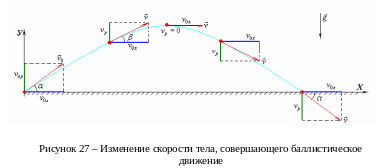
На подъеме вертикальная составляющая скорости уменьшается при постоянстве горизонтальной составляющей скорости. В верхней точке траектории вертикальная составляющая скорости становится равной нулю, и скорость в этой точке траектории равна горизонтальной составляющей . На спуске вертикальная составляющая скорости растет в противоположном направлении.

4 Найдем скорость тела в заданные моменты времени.

В момент времени t = 5 с:

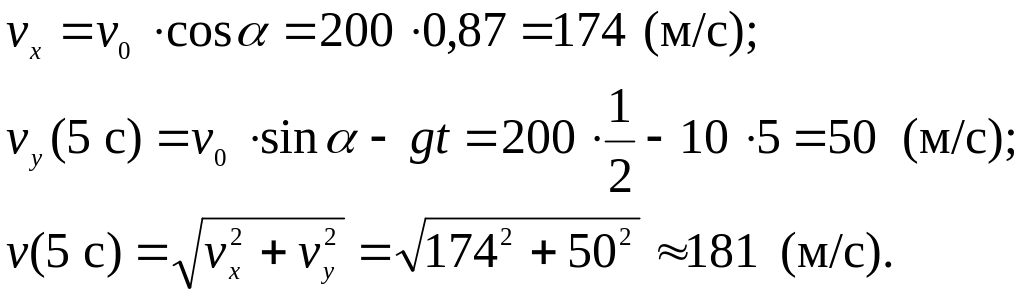
Направление скорости в момент времени t = 5 с:

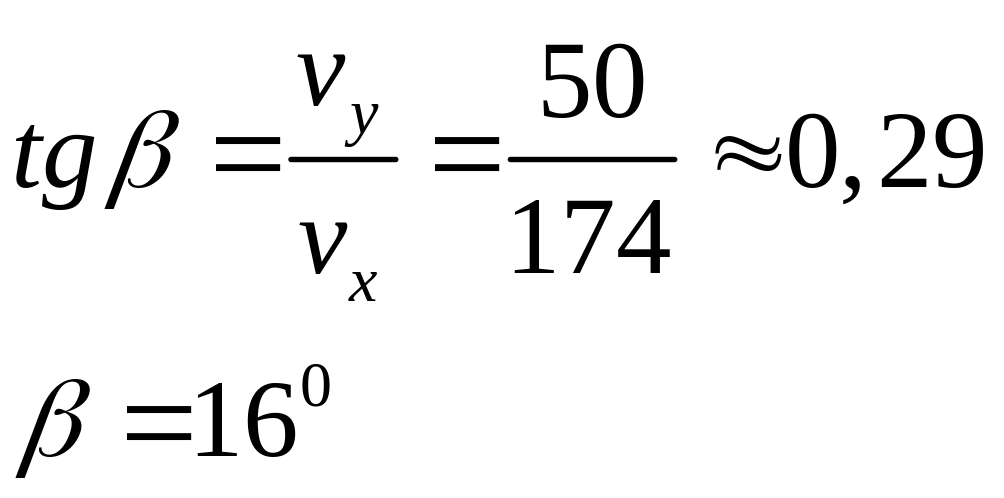
В момент времени t = 15 с:

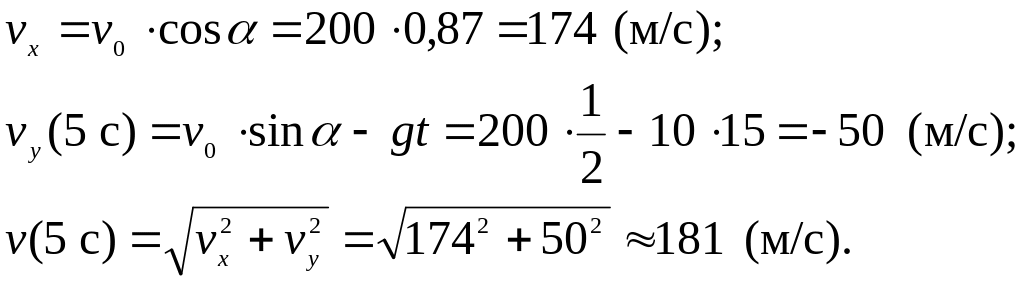
Направление скорости в момент времени t = 15 с:

.

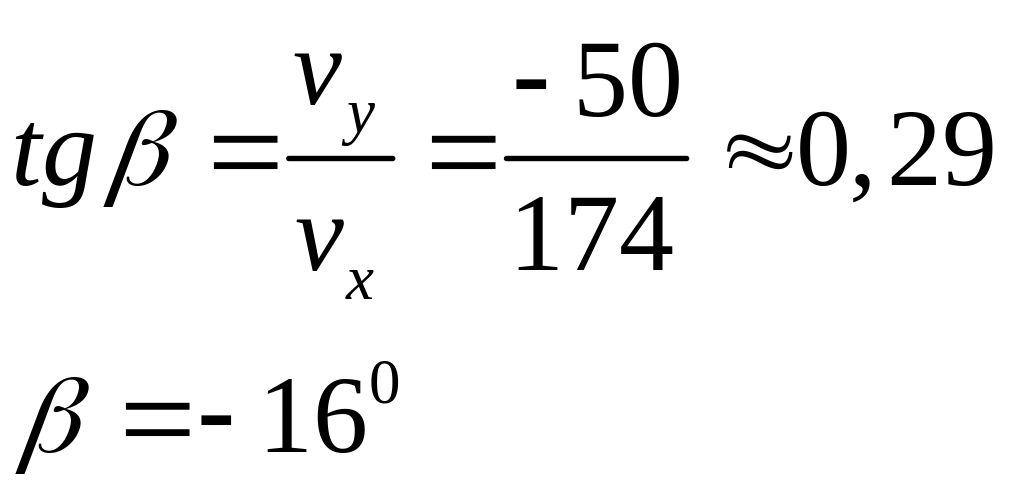Очевидно, что в момент времени t = 5 c снаряд поднимался, в момент времени t = 15 с снаряд находился на нисходящем участке траектории.

Пример 2 Высота подъема и дальность полета снаряда, вылетевшего из орудия под углом к горизонту

По условию предыдущей задачи запишите уравнения движения тела по осям OX и OY. По какой траектории двигается снаряд?

1 Запишем уравнения движения снаряда по горизонтали и вертикали

Равномерно движение по горизонтали

Равноускоренное движение по вертикали

2 Для определения траектории снаряда исключаем время из уравнений движения

.

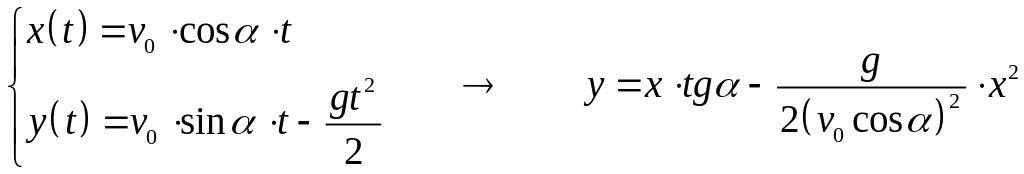Зависимость y(х) квадратичная, следовательно, траектория движения тела, брошенного под углом к горизонту – парабола.

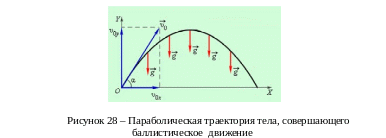
3 Максимальная высота подъема может быть найдена как тормозной путь по вертикали

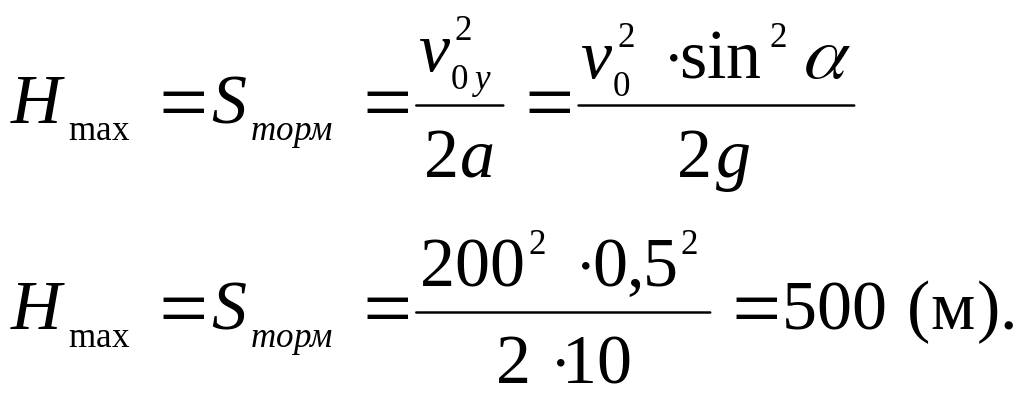
4 Дальность полета

.

Время полета может быть найдено двумя способами. В момент падения на землю координата у = 0. Тогда

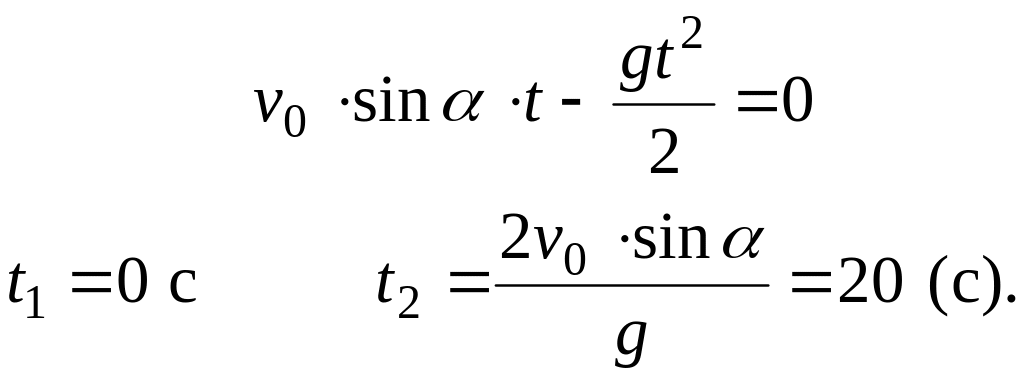
Второй способ нахождения времени полета:

Очевидно, что при падении на первоначальный уровень времена подъема и спуска одинаковы. Время подъема можно найти как время торможения по вертикали

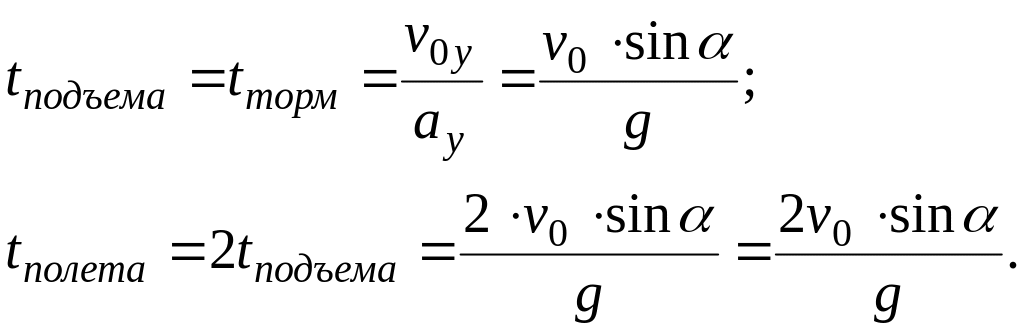
Дальность полета

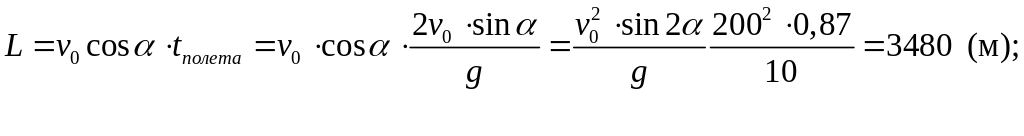
Проанализируем полученный результат для дальности полета.

. (8.1)

Дальность полета тела, падающего на первоначальный уровень:

1) прямо пропорциональна квадрату начальной скорости;

2) зависит от угла, под которым произведен бросок.

Очевидно, дальность полета будет максимальной, когда . Тогда угол .

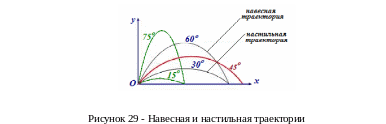
О днако, футболисты, равно как игроки в гольф, метатели копья и метатели диска, обычно используют траекторию, имеющую угол намного меньше – 30-35 градусов. Спортсмены выработали такую траекторию в результате длительной практики. Причина в том, что традиционная механика не учитывает особенности строения костей и мышечной структуры человеческого тела, а они позволяют приложить большую силу к мячу, который летит под более низким углом, чем под более высоким. Поэтому мяч, летящий под более низким углом, имеет более высокую скорость.

Понятно, что при углах бросания, меньших 45⁰, одинаковую дальность полета при одинаковой начальной скорости можно получить при двух разных углах бросания:

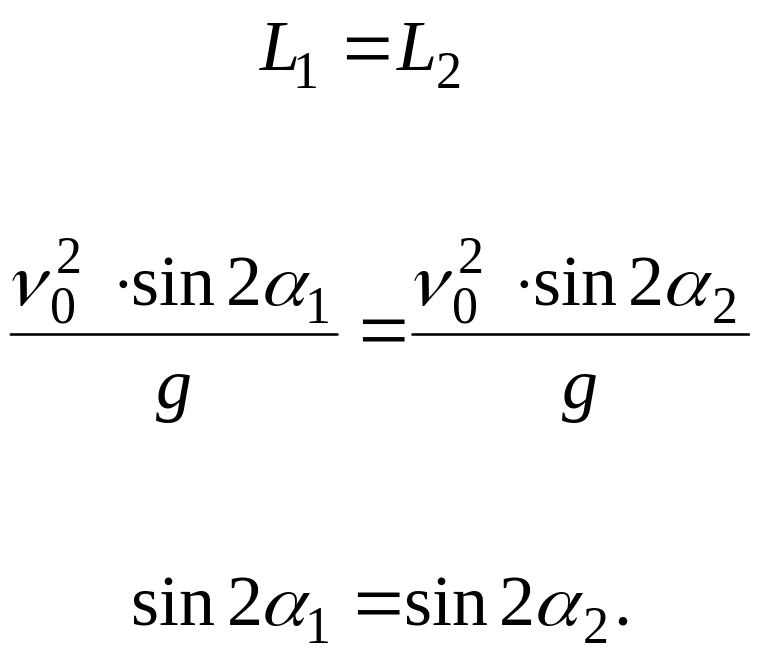
Последнее равенство возможно, когда . Следовательно, одинаковая дальность полета достигается при углах, дополняющих друг друга до 90⁰.

Пример 3 Треугольник скоростей

Сигнальная ракета выпущена со скоростью 30 м/с. Через 3,5 с после начала движения вектор скорости ракеты повернулся на 90⁰. Чему равна скорость сигнальной ракеты в этот момент?

Решение:

1 Полет ракеты происходит под действием силы тяжести. Ракета совершает равноускоренное движение с ускорением свободного падения .

2 При равноускоренном движении скорость линейно зависит от времени:

.

3 Построим треугольник скоростей, зная, что вектор направлен вертикально, а вектор скорости перпендикулярен начальной скорости .

4 По теореме Пифагора

Пример 4 Полет сигнальной ракеты

Под углом = 60⁰ к горизонту выпущена сигнальная ракета с начальной скоростью 40 м/с. Через какое время она будет двигаться под углом  =45⁰ к горизонту? Сопротивление воздуха отсутствует.

Р ешение:

Шаг 1 Скорость ракеты по горизонтали остается неизменной

Скорость ракеты по вертикали изменяется как при равноускоренном движении.

. (8.2)

Шаг 2 Вектор скорости составит угл 45° с горизонтом дважды – на подъеме и на спуске. Изобразим скорость в начальный момент времени и через время t.

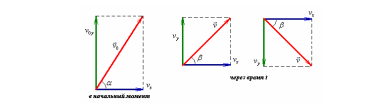
В начальный момент .

Через время t .

Шаг 3 Подставляем найденные графически значения вертикальных составляющих скорости в (8.2) и находим время:

.

На подъеме проекция скорости на вертикальную ось OY положительна. Время, через которое это произойдет, равно

,

.

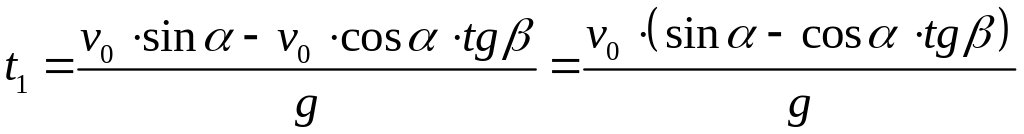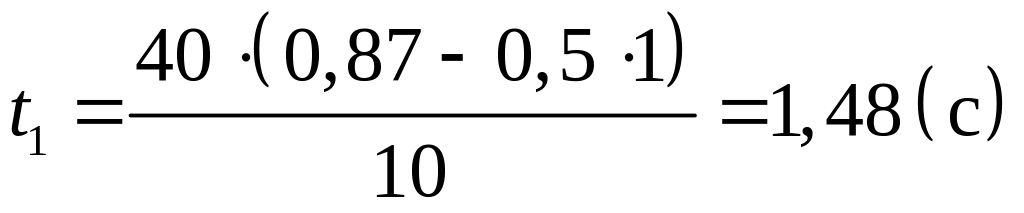На спуске, когда вектор скорости вновь составит с горизонталью угол 45°, проекция скорости на ось OY отрицательна. Время полета до этой точки траектории составляет

.

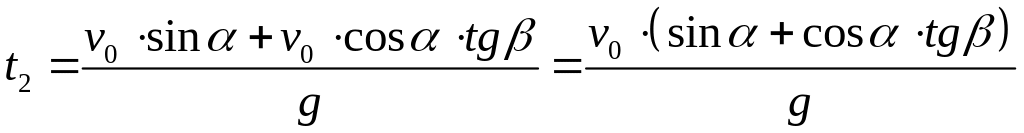
Можно было решить задачу векторным способом. В процессе полета скорость ракеты меняется оп закону .

Строим треугольники скоростей при движении ракеты вверх и движении ракеты вниз.

Для получившихся треугольников записываем теорему синусов.

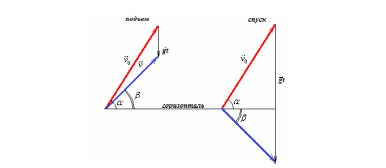
На подъеме

На спуске

Пример 5 Шарик «скачет» по горке

Маленький упругий шарик падает с высоты 50 см на горку, угол наклона которой α = 30⁰. Определите расстояние между точками, в которых произошли первые два удара шарика о горку.

Решение:

Шаг 1 Введем систему отсчета. Расположим координатные оси параллельно и перпендикулярно поверхности горки. Начало координат помести в точку первого удара шарика о горку. Начало отсчета времени – момент начала движения после первого удара.

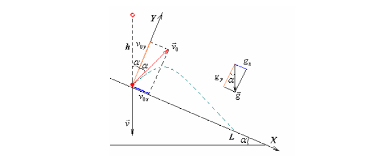
Шаг 2 Скорость шарика перед первым ударом о горку . После упругого удара модуль скорости остается неизменным . Направление скорости составляет угол α с осью ОУ.

Шаг 3 Записываем уравнение движения шарика по осям ОХ и ОУ после первого удара:

Шаг 4 Из уравнения движения по оси ОУ можно найти время между ударами. В момент второго соударения с горкой координата шарика по оси ОУ станет равной нулю:

,

.

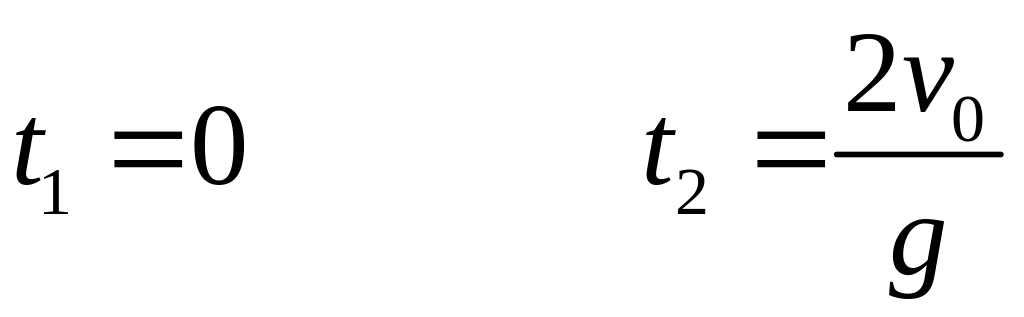Шаг 5 Подставляем время 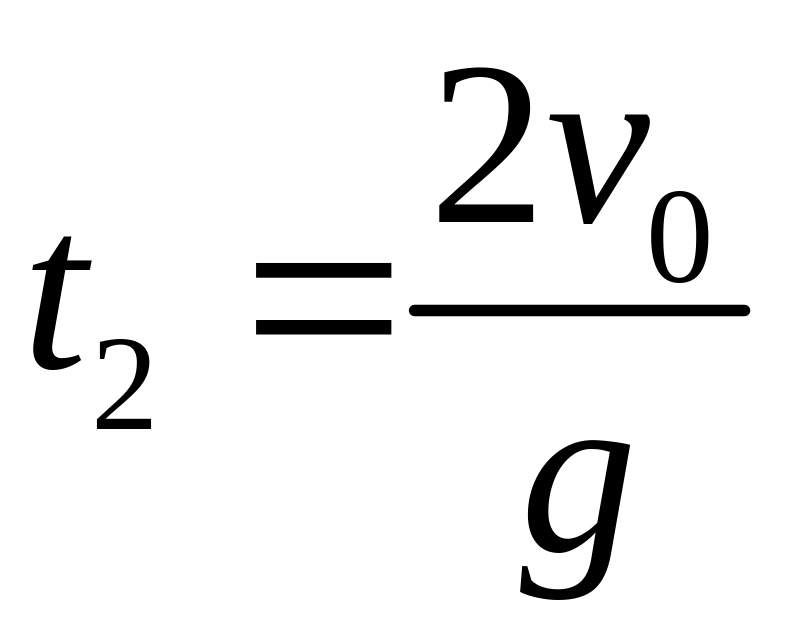в уравнение движения по оси ОХ и находим координату точки, в которой произойдет второе соударение шарика с горкой:

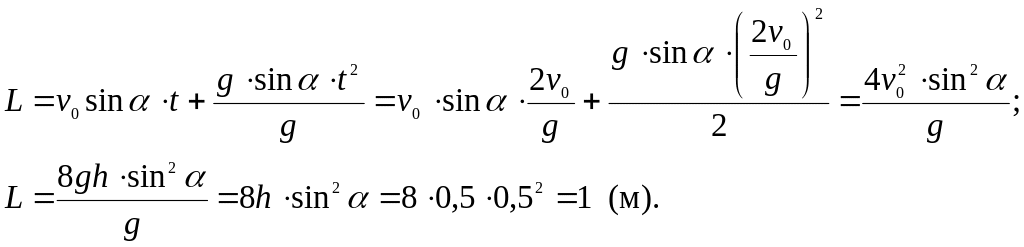
Очень часто рассмотрение движения тела, брошенного под углом к горизонту, выглядит проще и короче, если использовать векторный метод.

Пример 6 Треугольник перемещения

Условие: Граната, брошенная со скоростью 15 м/с, через 2 с упала на землю. Какова дальность полета гранаты, если она упала на первоначальный уровень?

Решение:

Шаг 1 Полет гранаты происходит под действием силы тяжести. Граната совершает равноускоренное движение с ускорением свободного падения .

Шаг 2 При равноускоренном движении перемещение зависит от времени по закону:

Шаг 3 Построим треугольник перемещения, зная, что вектор направлен вертикально, вектор сонаправлен с начальной скоростью, а вектор перемещения располагается горизонтально:

По теореме Пифагора

,

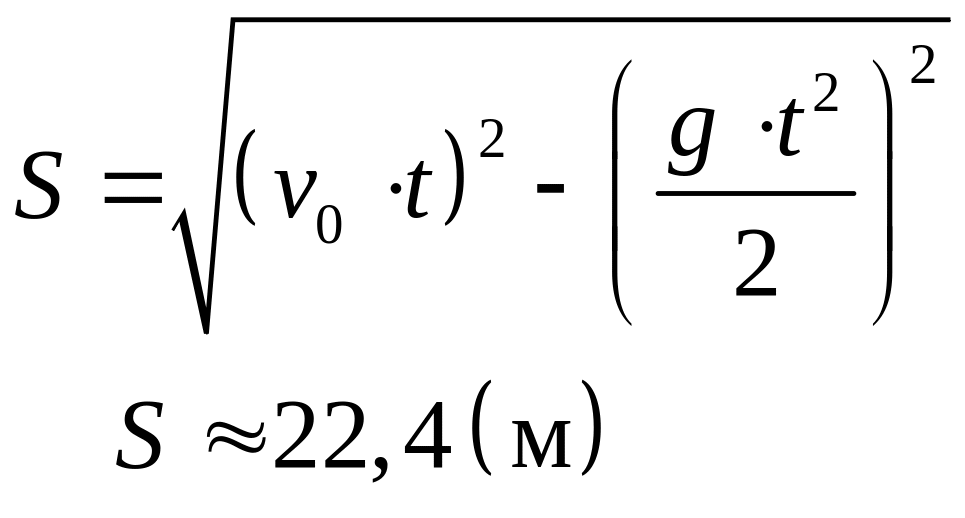Задачи для самостоятельного решения

(Во всех предлагаемых задачах сопротивлением пренебречь)

1 Долгое время рекорд мира по силе удара и скорости полета мяча в футболе принадлежал бразильскому нападающему Роберто Карлосу. Зафиксированная скорость полета футбольного мяча после удара Карлоса равнялась 198 км/ч. Сколько секунд длился полет мяча до его удара о землю, если он отправился в полет под углом 30⁰ к горизонту? Какова максимальная высота подъема мяча? Какова дальность полета?

2 В 1984 году, восточногерманский копьеметатель Уве Хон (Uwe Hohn) выполнил рекордный бросок на 104,80 м. Оцените начальную скорость копья, если принять, что оно отправилось в полет под углом 30⁰ к горизонту?

3 Камень, брошенный под углом к горизонту, достиг наибольшей высоты 20 м. Найдите время полета камня.

4 Диск, брошенный под углом 45⁰ к горизонту, достиг наибольшей высоты 15 м. Каковы начальная скорость диска и дальность его полета? Сопротивлением воздуха пренебречь. Через какое время диск оказался на высоте 10 м?

5 Во время обороны Севастополя в 1854 году русские войска применяли трехпудовую пушку. Калибр орудия составлял 273 миллиметра, наклон ствола достигал 9⁰, а начальная скорость полета снаряда - 357 м/с. Как долго находился в полете снаряд и на какое расстояние по горизонтали он перемещался, если стрельба производилась в обрыва высотой 15 м?

6 Сигнальная ракета выпущена под углом 60⁰ к горизонту со скоростью 40 м/с. Определите модуль и направление скорости ракеты через 2 с и через 5 с.

7 Баскетболист бросает мяч в кольцо. Сразу после отрыва от рук спортсмена скорость мяча составляет 8 м/с и направлена под углом  = 60⁰ к горизонту. С какой скоростью мяч попал в кольцо, если он долетел до него за секунду?

8 Под углом = 60⁰ к горизонту брошено тело с начальной скоростью 20 м/с. Через сколько времени оно будет двигаться под углом  =45⁰ к горизонту? Сопротивление воздуха отсутствует.

9 Начальная скорость брошенного камня равна 10 м/с, а спустя 0,5 с скорость камня равна 7 м/с. На какую максимальную высоту поднимется камень? Какова дальность полета камня, если он падает на первоначальный уровень?

10 Тело брошено под углом = 60⁰ к горизонту с начальной скоростью 10 м/с. Найдите скорость тела в тот момент, когда оно оказалось на высоте 3 м. Как направлена скорость в этот момент?

11 Шарик бросают под углом  = 30⁰ к горизонту с начальной скоростью 14 м/с. На расстоянии L = 11 м от точки бросания шарик упруго ударяется о вертикальную стенку. Где шарик упадет на землю?

12 Ядро, брошенное спортсменкой под углом 30⁰ к горизонту, дважды побывало на высоте : спустя 0,4 с и 1 с после начала движения. Найдите начальную скорость ядра и высоту .

13 Самолет пикирует на цель, находящуюся на земле, под углом 60⁰ к горизонту со скоростью 150 м/с и сбрасывает бомбу на высоте 600 м. На каком расстоянии в горизонтальном направлении от цели пилот сбросил бомбу, если она попала в цель?

14 Вертолет летит горизонтально со скоростью 160 км/ч на высоте 500 м. С вертолета нужно сбросить груз на теплоход, движущийся встречным курсом со скоростью 20 км/ч. На каком по горизонтали расстоянии от теплохода летчик должен сбросить груз?

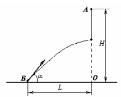
15 Из точки А, находящейся на высоте Н над поверхностью земли, свободно падает тело. Одновременно из точки В, находящейся на расстоянии от вертикали, проходящей через точку А, бросают второе тело так, чтобы они столкнулись в воздухе. Под каким углом к горизонту следует бросить второе тело? Какова должна быть его начальная скорость?

16 Мяч, упавший с высоты 1 м, два раза ударился о наклонно поставленную доску. Расстояние между точками удара мяча о доску 4 м. Удар абсолютно упругий. Определите угол между доской и горизонтом.