Добавил:

Mymnan Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет информатики и радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЗИвВС метода Кобяка.pdf

Скачиваний:

Добавлен:

15.09.2014

Размер:

1.05 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

где kj, – статистика элементарных событий, наблюдаемых через интервал

времени относительно отсчета t . Раскрывая скобки в левой и правой частях данного соотношения, а также упрощая полученное выражение, приходим к равенству

	k	1								s				s2
	k	1			kj kj,	1 1				s				s2			1
																					.
	j					4							l			2					.
	j	2j				4		4 2l 1					l			2		4
												2 1
Отсюда следует
														2
			1				1			s			s	2					j			(1.25)
	k		1	kj kj, j			1			s			s						j	.
	k			kj kj, j			4					l	1		2					.
		2					4		2l 1		2	l			2			2
											2

Из (1.25) можно получить два соотношения, характеризующих структурные свойства (взаимное расположение нулей и единиц) случайного сообщения. Во-первых,

kj kj, j

2l 1

2 2l

Откуда следует

для j.

Во-вторых,

2l 1

2 2l 1

kj kj,

(1.26)

(1.27)

Очевидно, что соотношение (1.27) согласуется с результатом (1.22), а равенство (1.26) исключает возможность группирования наборов элементарных событий в любой части псевдослучайной или случайной последовательности.

Таким образом, равенство (1.26) представляет собой второй критерий равномерности элементарных событий и предполагает выполнение условия (1.22) для пар наблюдаемых объектов. Кроме того, учитывая, что на параметр ограничения не налагаются, можно сделать вывод о возможности применения критерия (1.26) ко всем временным интервалам 1,n 1.

Рассмотрим далее частный случай формирования АКФ для временного интервала 0 .

1.8. Мгновенная эмпирическая дисперсия и доверительный интервал для вероятности наблюдения (0,1)-событий

Требуемое соотношение для дисперсии может быть получено из классического равенства для АКФ при 0:

Kˆ	j,	1	j	x t	M		2	,	x t 0,1 .
Kˆ	j,	j		x t	M		2	,	x t 0,1 .
x		j				x
			t 1

При n из данного равенства следует

Kˆ

x t x t M

x j

t 1

Таким образом, из формулы (1.26) для n могут быть получены равен-

ства вида

kj kj

k j

для j ,

2kj

(1.28)

Очевидно, что равенство (1.28) полностью повторяет предыдущие результаты, а, следовательно, соотношение для дисперсии в задаче синтеза миниасимптотического процесса имеет второстепенное значение.

Определим доверительный интервал для параметра p t p, отвечающий

доверительной вероятности 1 , учитывая динамику движения оценки к значению теоретического параметра. С этой целью запишем равенство

P k j pj

1
1
	k j j k j	1 .
j2	k j j k j	1 .
j2

Очевидно, что использованное в данном соотношении неравенство дает возможность записать пределы для вероятности в виде

kj j kj p

kj j kj

(1.29)

или

kj j

jp kj j

pqˆ ˆ

(1.30)

Отсюда можно определить величину границы для формулы (1.20). Действительно, учитывая формулы (1.29) и (1.30) и полагая, что требование (1.21) выполняется, имеем

s 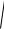kj j kj ,

kj 2l 1,

j 2l.

Из данного соотношения можно определить значение s по формуле

s 2l 1 ,

j n 2l.

Итак, при использовании М-последовательности в целях защиты информационных сетей необходимо, чтобы формируемые (0,1)-отсчеты удовлетворяли бы двум дополнительным требованиям:

1) эмпирическая вероятность наблюдения бернуллиевских событий в каждом такте формирования чисел должна стремиться к значению 0,5;

2) эмпирическая вероятность наблюдения пар бернуллиевских событий в каждом такте должна стремиться к произведению вероятностей 0,25 для любых сдвигов .

1.9. Вероятностные преобразователи информации

При решении задач, связанных с защитой информационных сетей, часто используют устройства, получившие название линейных преобразователей «код – вероятность». Классической схемой такого устройства является схема, представленная на рис.1.13. Функционирование схемы основывается на сравнении числа А и

случайного двоичного вектора X x1,x2,...,xl . Если случайные числа	X	имеют
равномерное распределение в диапазоне представления чисел A ,A ,A ,...,A			,
0 1	2	2l	1

то на выходе z формируетсядвоичная последовательность в соответствии с законом

	1	при A	j	X	,
z			j	i
z		при Aj Xi,				j const,
i	0	при Aj Xi,				j const,

где i– номер случайного числа.

А:	а1 а2 а3	аl
СИ	…		z

	Схема сравнения
	Схема сравнения

	…
X:	x1 x2 x3	xl
	Рис. 1.13

Вероятность единичного значения p z на выходе преобразователя в об-

щем случае может быть определена соотношением

p z Аj 2 l.

Более сложные устройства строятся с использованием двоичных счетчиков и применяются для интегрирования стохастических последовательностей. Структурная схема стохастического интегратора представлена на рис. 1.14.

Принцип действия таких устройств основывается на следующих математических законах. Если на вход счетчика подаются единичные случайные приращения, то величина интеграла за время t будет равна произведению

I 2 l p x t ,

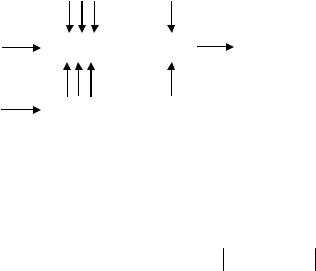
где l – разрядность счетчика,

p x –

вероятность единичного

значения во

входной последовательности.

При этом

l 1

0,5t

p x

k 2

2 l p x t

n 2

Содержимое накопителя <Cт2> в данной схеме определяется соотноше-

нием: Ст2 np x ,

ГСЧ

где x – единичное элементарное событие,

СИ

…

p(z)

n 2l – длина последовательности.

Доказательство следует из следующих

Схема сравнения

рассуждений. Очевидно, что при равномер-

…

ном

распределении

элементарных событий

p(x)

содержимое <Cт2>

будет

определяться

1 2 3 Ст 2 l

суммой единичных

приращений в каждом

такте, умноженных на вероятность этих

Рис. 1.14

приращений:

MСт2 x1p x1 x2p x2 x3p x3 ... xnp xn xi p xi

i 1

p xi p x p x xi np x .

i 1

Теперь, учитывая, что схема преобразователя вырабатывает значения выходной переменной z, используя l– разрядные равномерно распределенные случайные числа (счетчик рассматривается как база для сравнения), для вероятности p(z) будет справедливо соотношение

p zi	1	i n	1		l	np x .
		Ст2 i		MСт2 2
	l	Ст2 i	l	MСт2 2
	2		2

Полученная схема может быть модернизирована за счет введения отрицательной обратной связи. Это позволяет получить так называемый следящий режим, а соответствующее устройство получило название следящего интегратора

(рис. 1.15).

По цепи обратной связи сигналы выходной последовательности p(z) поступают на вход «–» реверсивного счетчика. В случае совпадения в среднем математических ожиданий последовательностей, действующих на входе и в цепи обратной связи, в схеме устанавливается динамическое равновесие.

Алгоритм генерирования чисел в последовательности p(z) определяется с учетом условия

1	при (Cт2)i (ГСЧ)i ,
zi 0	при (Cт2) (ГСЧ)		.
	i	i

		ГСЧ
			…	Y
	СИ			p(z)
	СИ	Схема сравнения
		Схема сравнения
p(x)			…	X
&		+ 1 2 3	…	l
		+ 1 2 3	…	l
&		–	Ст 2
&		–
		Рис. 1.15

Для математических ожиданий содержимого счетчика можно записать следующее рекуррентное соотношение:

p x

2l n, p x

p, i

Cт2,,i

Cт2,,i-1

где i– номер машинного такта.

Полагая, что в начальные моменты времени MCт2,0 0,

MCт2,1 p, выпи-

шем значения счетчика в последующие такты работы:

					1
MCт2,2 p p 1						,
MCт2,2 p p 1						,
					n
			1				1	2		(1.31)
MCт2,3	p	p 1		p		1			,
MCт2,3	p	p 1		p		1	n		,
			n				n

. . . . . . . . . . . . . . . . . . . .

MCт2,m p 1 a a2 ... am 2 am 1 ,	a 1	1	,
		n

где выражение в скобках есть сумма членов геометрической прогрессии со знаменателем а. При общем числе членов m из соотношений (1.31) получим

	1 am		1
MCт2,m p		p 1 am		np 1 am .
	1 a		1
			1 1

Сомножитель 1 am преобразуем к виду

1 a

1 e n.

Отсюда

p z 1 M n

		m

Cт2,m	p x 1 e n		m n n
			1
			1

		n
p x		1		(1.32)
		n
	1 e	n	.

Соотношение (1.32) показывает, что если входная случайная последовательность интегратора является стационарной, то процесс изменения содержимого реверсивного счетчика подчиняется экспоненциальному закону и переходные явления в устройстве затухают при n1 n.

1.10. Поточная шифросистема Д. Гиффорда

Поточная система шифрования Гиффорда получила распространение начиная с 1984 г. Основной элемент системы это 64-разрядный криптографический генератор с линейной обратной связью FB и нелинейной функцией выхода FF. Ключом сообщения является код начального заполнения регистра. Принципиально схема реализует шифрование путем наложения псевдослучайной гаммы на текст предварительно кодированного или открытого сообщения.

i 0,1 + В канал

	1		…	64

			FB-logic
+

		…
		…

Рис. 1.16

Однако практика применения показала, что данная система оказалась не достаточно стойкой к вскрытию. В частности, в печати имеются сведения о том, что расшифровка сообщений, закрытых с помощью схемы Гиффорда, требует в среднем 4 часа времени при использовании в целях декодирования 8 специальных станций (Sparc).

Тем не менее линейные регистры сдвига до настоящего времени применяются для различных компьютерных приложений, так как обладают рядом положительных свойств:

1)в схеме кодирования используются только простейшие операции сложения по модулю два и логического умножения;

2)высокое быстродействие создаваемых алгоритмов кодирования;

3)большое количество теоретических исследований, позволяющих использовать ГПСЧ в различных криптографических приложениях.

Алгоритм установления шифрованной связи между абонентами при использовании ГПСЧ состоит в следующем.

Для согласования работы своих шифрующих устройств абоненты договариваются о выборе числа g, так, чтобы выполнялось условие взаимной про-

стоты g,264 1 1.

После этого независимо друг от друга участники связи выбирают числаи из условия

1 , 264 1.

Далее первый из абонентов вычисляет значение g (mod264 ), а второй – g (mod 264), после чего они обмениваются результатами.

Зная число g (mod 264), первый абонент определяет ключ g (mod 264), а второй, зная g (mod 264), получает значение g (mod 264). Таким образом, оба абонента обладают одним и тем же ключом:

g (mod 264)=g (mod 264).

В заранее обусловленное время корреспонденты закладывают ключ в свои шифрующие устройства, что и позволяет достичь требуемого процесса синхронизации.

Сокращенный список примитивных полиномов по модулю два, используемых в целях шифрования, может быть представлен табл. 1.2.

						Таблица 1.2
		φ(x) = 1 + xj + xl

l	j или l–j	M = 2l–1	l	j или l–j		M = 2l–1

4	1	15	18		7	262143
5	2	31	20		3	1048575
6	1	63	21		2	2097151
7	1 или 3	127	22		1	4194303
9	4	511	23	5	или 9	8388607
10	3	1023	25	3	или 7	33554431
11	2	2047	28	3,9	или 13	268435455
15	1,4 или 7	32767	31	3,6,7 или 13		2147483647
17	3	131071	33		13	8589934591

Пример. Для полиномов степени l 23 можно составить следующие трехчлены:

x 1 x5 x23,

x 1 x9 x23.

Примечание. В случае если полином требуемой разрядности в таблице отсутствует, необходимо воспользоваться классическими первоисточниками литературы, например [23].

2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРНОЙ КРИПТОГРАФИИ

2.1. Криптосистема без передачи ключей

Основу данного метода криптографии составляют теоремы Эйлера и Ферма, а также алгоритмы решения сравнений первой степени, базирующиеся, в свою очередь, на алгоритме Евклида.

Сущность алгоритма Евклида состоит в отыскании нод(a,b) и заключается в следующем. Пусть a и b – положительные целые числа и a b. Тогда для указанных значений будут справедливы соотношения

a bq1 r2,	0 r2 b,
b r2q2 r3,	0 r3 r2,
r2 r3q3 r4,	0 r4 r3,

. . . . . . . . . . . .

rn 2 rn 1qn 1 rn,	0 rn rn 1,
rn 1 rnqn.

Алгоритм заканчивается при получении некоторого остатка rn 1 0. Наибольшим общим делителем тогда будетпоследний не равный нулю остаток rn .

Алгоритм Евклида можно представить также в виде следующих арифметических действий:

(525, 231)=21.

525

231

462

bq1

231

189

…

r2q2

rn-2

rn-1

r3q3

rn-1qn-1

qn-1

q4=2

n=4

…

n-1

rn qn

В теории существует математическая связь данного алгоритма и представления частного от деления двух чисел в виде полиномиальных дробей:

Ps qsPs 1 Ps 2 ,

Qs qsQs 1 Qs 2 ,

P0 1, Q0 0, Q1 1.

Из данных равенств следует

q ,

1 q2

q2 q

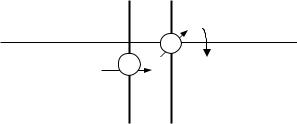
P4	q	1				, ...	Pn	q			1			a	.
	q					, ...		q							.
1				1				1			1
Q4		q2		1			Qn		q2		1			b
Q4		q2	q		1		Qn		q2	...		1		b
					1							1
													1
		3			q4								1
					q4							qn 1 q
												qn 1 q
													n

Обычно эти вычисления представляют в виде табл. 2.1.

Таблица 2.1

qs		q1	q2	…	qs-2	qs-1	qs	…	qn-1	qn

Ps	1	q1	P2	…	P	Ps-1	P	…	P	a
	1		P2		s-2		s		n-1

Qs	0	1	Q2	…	Qs-2	Qs-1	Qs	…	Qn-1	b

Пример. Пусть a 105, b 38, тогда в соответствии с алгоритмом Евклида значения q будут равны qs 2,1,3,4,2 , а табл. 2.1 примет вид

Таблица 2.2 s=0 s=1 s=2 s=3 s=4 s=5

qs		2		1	3	4	2
Ps		2			×
Ps	1	2	+	3	11	47	105

Qs	0	1		1	4	17	38

Из табл. 2.2 имеем:

			P1	q				2	,		P2	q			1		2				1		3	,		P3		q		1				2		1				11	,
				q					,			q					2							,		Q		q				1		2			1				,
			Q			1	1				Q		1		q					1 1						Q		1				1				1	1	4
		1								2						2									3					q2 q						1	3
P4		1								2						2						P5			3							3
		1											1					47												1		3						1							105
	q	1								2			1					47	,						q					1					2			1							105	.
	q					1				2			1						,						q					1					2							1				.
Q4	1					1							1			17						Q5			1					1												1		38
Q4		q2					1				1			1		17						Q5					q2					1					1					1		38
		q2									1																q2										1
					q								3																q										3
					q								3																q				1						3				1
		3					q4							4														3					1										1
							q4							4																	q4 q											4	2
																																5

Дальнейшее математическое обоснование криптосистемы без передачи ключей базируется на решении сравнений первой степени с одним неизвестным.

Для определения понятия «сравнение» будем рассматривать некоторые целые числа, представляющие собой остатки от деления на другое, заданное натуральное число m, которое назовем модулем.

Сравнимость чисел a и b по модулю m записывается в виде

a b mod m

и читается «a сравнимо с b по модулю m».

Сравнения обладают рядом свойств, характерных для обыкновенных равенств:

а) если два числа сравнимы с третьим, то все три числа сравнимы между собой по заданному модулю;

б) сравнения можно почленно складывать:

a1 b1	mod m , a2 b2 mod m ,	a3 b3	mod m , ... an bn	mod m ,
тогда
	a1 a2 a3 ... an b1 b2 b3		... bn mod m ;
в) слагаемое, стоящее в какой-либо части сравнения, можно переносить в
другую часть, переменив знак на противоположный:
	a b c mod m		a c b mod m .

Пример. 15 7 9 mod13 , 15 9 7 mod13 ;

г) к каждой части сравнения можно прибавить любое число, кратное модулю: a b mod m a nm b mod m ;

д) сравнения можно почленно перемножать:

a1 b1	mod m ,	a2 b2 mod m ,	a3 b3	mod m , ... an bn	mod m ,	(2.1)
	a1 a2	a3 ... an b1 b2	b3 ... bn	mod m ;

е) следствие из (2.1)

ak bk

mod m ;

ж) если выражения для многочленов А и В сравнимы по модулю m с некоторым числом w, то есть

A: a0xn a1xn 1 a2xn 2 ... anx0 w (modm),

B: b0xn b1xn 1 b2xn 2 ... bnx0 w (modm),

то сравнимы и сами многочлены А и В по модулю m:

n n

aixn i bixn i (modm) i 0 i 0

(данное свойство является обобщением предыдущих свойств сложения и умножения);

з) обе части сравнения и модуль можно умножить на одно и тоже число:

a b (mod m), ak bk (mod mk).

Рассмотрим теперь две теоремы, являющиеся базой для криптографического метода с закрытой системой ключей.

Теорема Эйлера. Пусть числа a и m взаимно простые, то есть a,m 1,

тогда будет справедливо равенство

a m 1 (mod m), m 1,

где m – это функция Эйлера, которая показывает число чисел взаимно про-

стых с m с учетом 1. Считается, что 1 тоже обладает взаимной простотой с m. Пример. 6 2, так как в ряду 1,2,3,4,5 только два числа 1 и 5 считают-

ся взаимно простыми с числом 6. Соответственно:

7 6 1 (mod 6).

Теорема Ферма. Если p– простое число, а число a не делится на p, то есть a sp, и тогда имеет место сравнение вида

ap 1 1 (mod p),

где p p 1. Например 9 7 6 1 (mod 7).

Приведенные две теоремы в задачах криптографии применяются для решения сравнений, корни которых используются для выбора секретных ключей.

Пусть требуется решить сравнение первой степени с одним неизвестным:

		ax b (modm),	(a,m) 1.	(2.2)
	Принцип решения сравнения (2.2) основывается на разложении отноше-
ния	m	в непрерывную (полиномиальную)	дробь. Согласно свойствам непре-
	a

рывных дробей, можно записать

PsQs 1 Ps 1Qs ( 1)s .

Тогда, рассматривая две последние подходящие дроби, имеем

Pn 1 , Pn m, mQn 1 aPn 1 1 n.

Qn 1 Qn a

Отсюда следует, что

aP	1 n 1			(mod m),
n 1
a 1 n 1 Pn 1b b (mod m),	x	b	mod m ,
a 1 n 1 Pn 1b b (mod m),	x		mod m ,
		a
x 1 n 1	Pn 1b			(mod m) .

x a 1 n 1 Pn 1b mod m , (2.3) a

Итак, для решения сравнения (2.2) необходимо определить только числитель n 1 подходящей дроби, согласно алгоритму Евклида, и подставить его в решение (2.3).

Пример. Решить сравнение вида 111x 75 (mod 321). Для решения поставленной задачи необходимо указать на то, что

111,321 3,

111 37 3,

321 107 3.

Таким образом, начальный вариант сравнения можно сократить на 3, откуда следует

37x 25 (mod 107).

(2.4)

Разложим отношение 107 в непрерывную дробь и составим табл. 2.3 для

числителей Ps .

									107			37					Таблица 2.3
											74
							37					2
												2
										33				s=0	s=1	s=2	s=3	s=4
										33				s=0	s=1	s=2	s=3	s=4
								33
										1
		33								1			qs		2	1	8	4
						4
						4
				32
						8
4						8							Ps	1	2	3	26	107
					1
					1
	4
	4		4

0

Для данного примера n 4, P3 26, b 25. Следовательно, решение сравнения (2.4) может быть представлено в виде

x 1 3 26 25 99 (mod107) .

Решением исходного сравнения будут три корня вида

x 99 k 107 (mod 321), k 0,1,2; x 99, 206, 313 (mod 321).

Криптографический метод на основе теорем Эйлера и Ферма основывает-

ся на следующем утверждении.	Если число p–простое, а число
Следствие из теоремы Ферма.
0 p 1, то существует такое k 1 (mod p 1), при котором
k	(mod p).

Итак, пусть абоненты А и В условились организовать между собой секретную от наблюдателя С переписку. С этой целью они выбирают достаточно большое простое число p, такое, что значение p 1 хорошо разлагается на большое число сомножителей. Каждый из абонентов независимо один от дру-

гого выбирает числа-ключи a и b и сопутствующие им неслучайные параметры и из условия

a 1 mod p 1 ,	0 p 1;
b 1 mod p 1 ,	0 p 1.

Таким образом, абонент А обладает своими секретными ключами a и , неизвестными абоненту В, а абонент В обладает секретными ключами b и, неизвестными абоненту А. В данной постановке задачи очевиден факт

a b 1 mod p 1 .

Пусть абонент А решает передать сообщение (заметим, что не все кодируются данным методом) абоненту В, причем 0 p 1. Тогда А зашифровывает сообщение своим первым секретным ключом, находит шифротекст

	(mod p),	0 p
1		1

и отправляет его абоненту В.

Приняв шифротекст, абонент В, в свою очередь зашифровывает сообщение 1 своим первым секретным ключом

	2		(mod p),	0	2	p
	2	1			2

и пересылает его обратно абоненту А. Абонент А, получив обратно свое теперь уже дважды шифрованное сообщение, шифрует его в третий раз своим вторым ключом

3 2a (mod p),

0 3 p

и вновь отправляет его абоненту В. Последний расшифровывает это сообщение при помощи своего второго ключа

3b (mod p),

0 4

p .

Действительно, последнее равенство может быть записано в виде

4 ab k (mod p),

а так как ab k 1(mod p 1), то k (mod p) или 4 (mod p).

Пример. Абоненты А и В решили установить между собой защищенную от наблюдателя С связь без передачи ключей с простым модулем p 23.

Абонент А выбирает случайным образом число a 5 и находит к нему неслучайный параметр , решая сравнение 5 1 (mod (23)); 9. Следовательно, числа 5 и 9 – секретные ключи абонента А.

Абонент B выбирает случайным образом число b 7 и находит к нему неслучайный параметр , решая сравнение 7 1 (mod (23)); 19. Следовательно, числа 7 и 19 – секретные ключи абонента B.

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.09.201459.39 Кб8Билеты к ГОСам Дневное отделение 2014.doc
#
15.09.201452.39 Кб8задание по авмис на 9сем.docx
#
15.09.20142.68 Mб24Задания и примеры от Клевакина. Часть 1..pdf
#
15.09.201438.4 Кб3Задания по ЗИвВС.doc
#
15.09.201425.6 Кб3Заявление на тему диплома.doc
#
15.09.20141.05 Mб34ЗИвВС метода Кобяка.pdf
#
15.09.2014510.87 Кб18ОБРАЗЕЦ ЧАСТИ КУРСОВОГО.docx
#
15.09.20145.74 Кб6ТЗ для Контрольной 8 семестр (Петровский).docx
#
15.09.2014510.87 Кб13Файл с оформлением курсача (если у кого нет).docx