V. Группировка наблюдений

Если объём выборки очень велик, то обрабатывать весь массив собранных данных бывает иногда затруднительно. С целью облегчить вычислительную работу в таких случаях производят так называемую группировку наблюдений. Она бывает также необходима для некоторых статистических процедур.

Представим выборку (x₁, x₂, ¼ , x_n) в виде вариационного ряда: y₁£y₂£ £¼£y_n. Величина y_ny₁ называется размахом выборки. Разобьём отрезок [y₁, y_n] на N равных частей длины D .

Поскольку неизбежно округление данных, следует договориться о концах интервалов: разбиваем весь отрезок [y₁, y_n] на отрезки

D_k[x_k^o , x_k^o ),

где x_k^o – середина k-ого полузакрытого интервала. При таком разбиении последний интервал берём в виде

D_N[x_N^o , x_N^o ].

Обозначим через m_k число наблюдений, попавших в k-й интервал D_k. Числа  x₁^ox₂^o¼x_N^o называют интервальным вариационным рядом, m_k – приписанные этим точкам частоты.

В принципе, можно строить интервальный вариационный ряд, производя, если это нужно, разбиение и на неравные интервалы.

Вся дальнейшая работа (например, построение эмпирической функции распределения, оценки и т. д.) осуществляется уже с интервальным вариационным рядом. При этом нужно не забывать, что группировка вносит в статистические вычисления дополнительную ошибку – ошибку на группировку.

Число интервалов N выбирают так, чтобы частоты m_k были достаточно велики, а само число N не слишком велико.

Разбиение на неравные интервалы производят в том случае, если на оси x есть области очень бедные попавшими туда наблюдениями.

VI. Оценка плотности вероятности

Пусть X – непрерывная случайная величина с плотностью вероятности p(x) (рис. 4). Требуется найти эту плотность, хотя бы приближённо, в точке x.

Пусть D – произвольный достаточно малый интервал с центром в точке x.

Очевидно, если интервал D достаточно мал, а x – точка непрерывности плотности p(x), то

P{XÎD} p(x)dx»p(x)×D.

Здесь буквой D мы обозначили и интервал как множество точек, и его длину.

Отсюда:

p(x)» ×P{XÎD},                    (*)

причём ошибка этого приближения тем меньше, чем меньше D.

Стоящую в (*) вероятность P{XÎD} мы умеем приближённо оценивать частотой события {XÎD}: P{XÎD}» где , m_D – число наблюдений в выборке, попавших в интервал D. Ошибка этого приближения в среднем тем меньше, чем больше n и m_D, а для того, чтобы m_D было достаточно велико, нужно, чтобы интервал D был не слишком мал (иначе вероятность попасть в него при наблюдениях будет мала).

Итак:

p(x)» ,

и процедура оценки плотности выглядит следующим образом: производим группировку наблюдений и по интервальному вариационному ряду находим оценку плотности p(x) в точках x_k^o:

p(x_k^o)» .

Графически можно отложить ординаты длины в абсциссах x_k^o. Далее появляются две возможности: можно либо соединить полученные точки ломаной линией – получим полигон частот (рис. 5), либо провести через них горизонтальные отрезки – получим гистограмму (рис. 6).

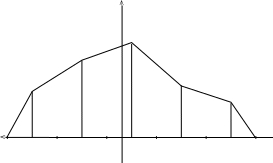
 y₁  x₁^o      x₂^o                      x_n^o  y_n  x

Рис. 5. Полигон частот.

y₁  x₁^o      x₂^o                      x_n^o  y_n  x

Рис. 6. Гистограмма.

Полигон и гистограмма и дают приближение для плотности p(x). Закон больших чисел Бернулли и общеизвестные теоремы математического анализа позволяют утверждать, что в точках непрерывности плотности p(x) отклонения от неё гистограммы и полигона будут как угодно малы со сколь угодно большой вероятностью при достаточно больших n и N и достаточно малом D. Нужно помнить, что, с одной стороны, D нужно делать малым, чтобы уменьшить ошибку от замены интеграла площадью ступеньки, а с другой стороны, нельзя взять D слишком малым, чтобы не увеличить вероятностную ошибку от замены вероятности на относительную частоту.

 y₁  x₁^o      x₂^o                      x_n^o  y_n  x