Алгоритм Фибоначчи-1

Начальный этап

(1) Задать константу , начальный интервал [a₁, b₁], длину конечного интервала L_n и определить число n так, чтобы выполнялось условие F_n > (b₁ - a₁)/L_n.

(2) Взять две пробные точки ₁ = a₁ + (F_n-2/F_n)(b₁ - a₁) и ₁ = a₁ + (F_n-1/F_n)(b₁-a₁). Положить k = 1.

Основной этап

Шаг 1. Сократить текущий интервал локализации:

(1) Если f(_k) < f(_k), то положить a_k+1 = a_k, b_k+1 = _k,_k+1 =_k и вычислить новую точку _k+1 = a_k+1 + (F_n-k-2/F_n-k)L_k+1, где L_k+1 = b_k+1 - a_k+1; перейти на шаг 2.

(2) Если f(_k)>> f(_k),то положить a_k+1 =_k, b_k+1 = b_k, _k+1 = _k и вычислить _k+1 = a_k+1 + (F_n-k-1/F_n-k) L_k+1.

Шаг 2. Проверить критерий окончания поиска:

(1) Заменить k на k+1. (2) Если k = n - 1, перейти на шаг 3, иначе - на шаг 1.

Шаг 3. Найти аппроксимирующий минимум х^(*):

(1) Положить _k = _k + .

(2) Если f(_k) > f(_k), то x^(*) = (_k + b_k)/2. В противном случае - x^(*) = (a_k + _k)/2.

Метод Давидона

Начальный этап

1. Выбрать ε, x⁰, p, α₁

2. Предполагается, что сработал метод Свенна и получен интервал [a, b].

Основной этап

1. Найти аппроксимирующий минимум, т.е. точку d по формулам:

2. Проверить КОП: если y`<sub>r</sub>≤ ε, то остановиться, х=a+α<sub>r</sub>p. Иначе: сократить ТИЛ: если y`_r <0, то [r,b], если y`_r >0, то [a,r].

Положить k=k+1 и вернуться на шаг 1.

Блок-схемы

Метод Свенна

Метод ЗС-1

Метод Фибоначчи-1

Метод квадратичной интерполяции – экстраполяции

Метод Давидона

Текст программ на языке С++

Исследование методов одномерного поиска минимума унимодальной функции

Метод Свенн – метод Ньютона

Спецификация программы:

a, b – текущий интервала локализации

h – размер шага

min –минимум

x1 – стартовая точка

k, k1 – счетчики числа итераций.

Текст программы:

#include<conio.h>

#include <math.h>

#include <iostream.h>

long double a,b;

int k1, k;

double fx(double x) // функции

{

// возрат в зависимocти от x

if(x>=0)

return (4*x*x*x-3*x*x*x*x);

else

return (4*x*x*x+3*x*x*x*x);

}

double dif(double x) // производные для ньютона

{ if(x>=0)

return (12*x*x-12*x*x*x);

else

return (12*x*x+12*x*x*x);

}

double dif2(double x)

{ if(x>=0) return (24*x-36*x*x);

else return (24*x+36*x*x);

}

double Sven(long double x1, long double x2, long double h)

{ // Метод Свенн

long double x3,z;

x2=x1+h;

while (1)

{

h=2*h;

x3=x2+h;

if (fx(x3)>fx(x2))

break;

x1=x2;

x2=x3;

k1=k1+1;

}

a=x1;

b=x3;

if(a>b) //a– всегда слева,b- справа

{

z=b;

b=a;

a=z;

}

return h;

}

void main()

{

clrscr();

double x1,x2,h=0.01,e=0.001;

x1=0.4; //Начальная точка

x2=x1+h;

cout<<"\nNach tochka x1: "<<x1;

if ( fx(x2) > fx(x1))

{

h=-h; // меняем знак если функция растет

x2=x1+h;

}

h=Sven (x1,x2,h);

cout << "\n\nsSchag svenn. k= " << k1;

cout << "\nInterval posle Svenn";

cout << "\na= " << a << endl;

cout << "b= " << b << endl;

do // Ньютон

{

x1=a;

x2=b;

x1=x2-dif(x2)/dif2(x2);

k++;

cout<<"\nx1-x2;

}

while(fabs(x1-x2)>e && fabs(dif(x1))>e);

cout << "\n\nsSchag Nuton. k= " << k;

cout << "\n\nMinimum= " << x1;

getch();

}

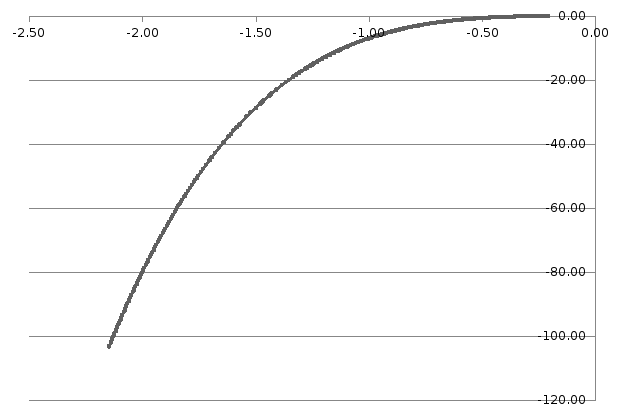
Результаты работы программы

интервал по Свенну: -2.15 … -0.23

число повторений цикла после установления интервала k=6

минимум функций по Ньютону 1.000000

число повторений цикла после установления интервала k=4

График функции