
Отчет лаба 2
.docxФедеральное агентство по образованию

Санкт-Петербургский государственный
электротехнический университет «ЛЭТИ»

Кафедра САПР
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 2
«Исследование методов полиномиальной интерполяции
для поиска минимума целевых функций»
Выполнил: .
Группа:
Проверил:
(Ф.И.О.)
Санкт-Петербург
2012
Оглавление:
Задание…………………………………………………………………………….3
Описание методов оптимизации…………………………………………………3
Блок-схема программы………………………………………………………..…5
Спецификация программы……………………………………………………….6
Текст программы ………………………………………………………………....6
Результаты тестирования…………………….………….……………………….9
Графическая интерполяция………………………………………………………9
Выводы…………………………………………………………………………..10
Ответы на контрольные вопросы………………………………………………10
Задание:
Целью работы - сравнение двух методов одномерной минимизации - прямого и интерполяционного; разработка программы, реализующей прямой метод на этапе установления границ начального интервала и метод полиномиальной интерполяции для локализации искомого минимума.
Описание методов оптимизации:
Метод Свенна:
С помощью этого метода получаем начальный интервал локализации минимума.
Начальный этап:
1) задать x0 – произвольная начальная точка.
2) выбрать шаг h равным 0.001 или 0.01*|x0|.
Основной этап:
Шаг 1:
Установить направление убывания целевой функции. Для этого надо взять x2=x1+h. Если f1<f2, то надо поменять направление движения(h=-h и взять x2=x1+h).
Шаг 2:
Вычислять fk в точках xk+1=xk+hk, где hk=2hk-1, k=2,3,…,n-1 до тех пор пока не придём в точку xn такую что fn>fn-1.
Шаг 3:
Установить начальный интервал локализации минимума a1=xn-2 и b1=xn.
Метод золотого сечения-1
Более эффективный чем дихотомия по числу операций. Дихотомия за 100 вычислений сокращает интервал в 14 раз, а ЗС в 11 раз.
Начальный этап:
-
Получить a1 и b1 методом Свенна
-
Получит значение x1
-
Взять λ1 = a1+t1*L1
Основной этап:
Шаг 1:
Если f1=f(λk)< f2=f(ηk) то ak+1=ak, bk+1= ηk, λk+1 = ak+1+0,318* Lk+1
Шаг 2:
Если f1< f2, то ak+1= λk, bk+1= bk, λk+1 = ηk, ηk+1 = ak+1+0,618* Lk+1
Метод экстраполяции-интерполяции
Самые неточные методы.
Начальный этап:
-
Получить a1 и b1 методом Свенна
-
Взять центральную точку и две соседние с не на расстоянии h.
Основной этап:
Шаг 1:
Взять 3 точки b=x0, a=b-h, c=b+h, найти аппроксимацию min.
Шаг 2:
Критерий окончания поиска
if ((d-b/b) ε и (fd-fb)/fb ε2, то аппроксимация min будет x=(d+b)/2
иначе фиксируем новую точку как стартовую и возвращаемся на шаг 1.
Начало
h=0.01; x1=4; x2=x1+h; if(fx(x2)>fx(x1)) h=-h; x2=x1+h; Да Нет h=Svenn(x1,
x2, h); cout<<a; cout<<b; min
= zs1(a,b); cout<<min; c=(a+b)/2














min=inter(a,b,c);

min=fabs(min); cout<<min;

Конец
Спецификация программы.
a, b – текущий интервала локализации
c – третья точка
h – размер шага
min –минимум
x1 – стартовая точка
k, k1, k2 – счетчики числа итераций.
Текст программы:
#include <iostream.h>
#include <math.h>
#include <stdio.h>
#include <iostream.h>
#include <conio.h>
double a,b,c;
double x1,x2,h,h1,min;
int k, k1, k2; // счетчик циклов
double t1=(sqrt(5.0)-1)/2;
double t2=(3-sqrt(5.0))/2;
double fx(double x) // заданная функция
{
return (x*x+2*x);
}
double Sven (double x1, double x2, double h)
{ // Метод Свенн
long double x3,z;
x2=x1+h;
k1=1;
while (1)
{
h=2*h;
x3=x2+h;
if (fx(x3)>fx(x2))
break;
x1=x2;
x2=x3;
k1=k1+1;
}
a=x1;
b=x3;
if (a>b) // перестановка для: а - всегда слева, b - справа
{
z=b;
b=a;
a=z;
}
return h;
}
double zs1(double a, double b) //Метод золотое сечение-1
{
double e,m,y,min;
y=a+t1*fabs(a-b);
m=a+t2*fabs(a-b);
k=1;
e=0.1;
while(fabs(a-b)>e)
{
if (fx(y)<fx(m))
{
b=m;
m=y;
y=a+t2*fabs(a-b);
}
else
{
a=y;
y=m;
m=a+t1*fabs(a-b);
}
k++;
}
min=(a+b)/2;
return min;
}
double inter(double a,double b,double c)
{
double fa,fb,fc;
fa=fx(a);
fb=fx(b);
fc=fx(c);
return (0.5*(fa*(b*b-c*c)+fb*(c*c-a*a)+fc*(a*a-b*b))/(fa*(b-c)+fb*(c-a)+fc*(a-b)));
} ;
void main()
{
clrscr();
h=0.01;
x1=4;
x2=x1+h;
if(fx(x2)>fx(x1))
{h=-h;
x2=x1+h;
}
h=Sven(x1,x2,h);
cout<<"\na = "<<a; //Получили a и b после Свенна
cout<<"\nb = "<<b;
min=zs1(a,b); // Золотое сечение 1
cout<<"\n\nZolotoe sechenie-1. k= "<<k;
cout<<"\nminimum = "<<min;
c=(a+b)/2; // Задаем 3 точку
min=inter(a,b,c);
min=fabs(min);
cout<<"\n\nInter";
cout<<"\nminimum = "<<min;
getch();
}
Результаты тестирования различных методов:
Ниже приведены таблицы с результатами работы программы для двух методов, с различными стартовыми точками и точностями вычисления.
|
Точность: |
|
0.01 |
|
X1=4 |
К |
X* |
|
Метод Свенна |
10 |
[-6,23;1,45] |
|
Метод интерполяция |
1 |
1 |
|
Точность: |
|
0.001 |
|
X1=4 |
К |
X* |
|
Метод Свенна |
10 |
[-6,227;1,451] |
|
Метод интерполяция |
1 |
1 |
График функции
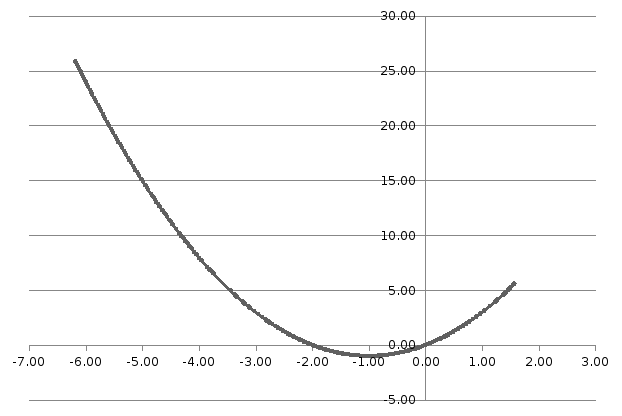
Выводы:
В данной лабораторной работе мы сравнили два метода:
1) прямой метод на этапе установления границ начального интервала
2) интерполяционный метод интерполяции для локализации исходного минимума.
При выборе начальной точки близкой к истинному минимуму интерполяционный метод работает в 3 раза быстрее прямого метода. Однако, если взять начальную точку далеко от истинного минимума, то метод интерполяции намного уступает прямому методу. Если интервал невелик и можно установить значение начальной точки поиска, то следует использовать интерполяционный метод, если же интервал велик и выбрать близкое значение начальной точки сложно, то стоит использовать линейный метод поиска минимума.
Ответы на контрольные вопросы:
1.Когда целесообразно использовать методы полиномиальной интерполяции?
Целесообразно их использовать при выполнении сначала метода одномерной минимизации унимодальной функции (например дихотомии), а затем уже на полученном интервале искать минимум методом полиномиальной интерполяции.
2. Сравните организацию поиска в методах ДСК и Пауэлла.
Метод Пауэлла отличается от метода ДСК тем, что стартует из трех равноотстающих точек, но на второй и последующих интерациях условия |b-a|=|c-b| нарушается. И отстутствует возврат с уменьшенным вдвое шагом.
3. Как строится система из 4-х уровнений в методе кубической интерполяции?
Fa = Qa=D Fb=Qb=Ab3+Bb2+Cb+D
F/a= Q/a=C
F/b= Q/b=3Ab2+2Bb+C где Q заданная функция Ax3+Bx2+Cx+D
4.Достоинства и недостатки методов интерполяции в задачах оптимизации?
Достоинства: в отличие от золотого сечения в методах интерполяции учитывается разность значений функции и как следствие ускоряет поиск на заключительных итераций
Недостатки: выигрыш достигается ценой ограничений на f(x) которая должна быть гладкой (т.е. допускается производная и функция не имеет разрыва)
5. Почему при минимизации целевых функций используют комбинированные стратегии поиска?
Комбинированные стратегии поиска используют для ускорения поиска минимума,т.к. наиболее быстрые методы поиска ищут в основном не так точно, а более точные не так быстро, поэтому сначала лучше найти более грубо, но уже больее меньший, чем начальный, но зато второй метод, требующий более большое время вычисления найдет ответ более точно и быстро.
-
Выполните одну итерацию метода ДСК при поиске минимума f(x) = x2 - x, x = 3.
Предположим, что сработал метод Свенна2 и за 12 итераций мы узнали 3 точки a= -0.039 b=0.473 c=0.986 . Ищем апроксимационный минимум d = 0.3585 Далее мы берем лучшую точку из b и d. В данном случае это b. И строим 2 симметричные относительно нее точки a=b-h и c=b+h Уменьшаем h=h/2. Проверяем КОП и возвращаемся на шаг 1.
